pRefCell的选择将修改压力修正方程矩阵对应的系数
-
各位Foamer好,在探究压力修正方程矩阵系数的过程中,发现一个有意思的点,从而产生一个疑问。
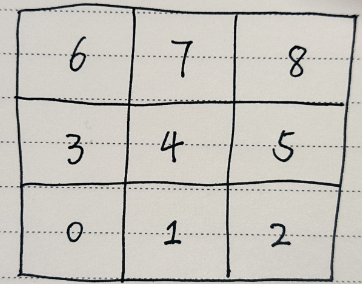
本人使用SimpleFoam计算方腔流,网格为3*3(这样好看矩阵的系数),如下加入的代码为压力修正方程系数的输出:fvScalarMatrix pEqn ( fvm::laplacian(rAtU(), p) == fvc::div(phiHbyA) ); pEqn.setReference(pRefCell, pRefValue); ///////////////////////////////////////////////////////////////////////////////////// /* */ std::vector<std::vector<double>> P(mesh.nCells(), std::vector<double>(mesh.nCells(), 0.0)); for(label i=0; i<mesh.nCells(); i++) { P[i][i] = pEqn.diag()[i]; } for(label faceI=0; faceI<pEqn.lduAddr().lowerAddr().size(); faceI++) { label l = pEqn.lduAddr().lowerAddr()[faceI]; label u = pEqn.lduAddr().upperAddr()[faceI]; P[l][u] = pEqn.upper()[faceI]; P[u][l] = pEqn.lower()[faceI]; } Info << "P before boundary influence:\n" << endl; for (int i = 0; i < mesh.nCells(); i++) { Info << "["; for (int j = 0; j < mesh.nCells(); j++) { Info << P[i][j] << " "; } Info <<"]"<< endl; } Info << endl;有意思的现象是 当我的pRefCell取网格单元0时,其矩阵系数如下
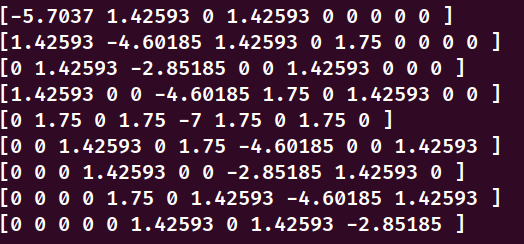
0号网格单元的对应的对角矩阵系数等于其余影响的单元系数负数之和的两倍(-5.7037 = -2*(1.42593+1.42593))
但是其余的网格单元对应的对角矩阵系数等于其余影响的单元系数之负和如果将pRefCell选为1时,那么矩阵系数如下
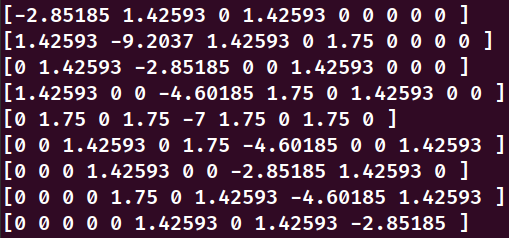
有意思的点来了,1号网格单元的对应的对角矩阵系数等于其余影响的单元系数负数之和的两倍(-9.2037 = -2*(1.42593+1.42593+1.75))
其余的网格单元对应的对角矩阵系数等于其余影响的单元系数之负和有大佬知道为什么这么处理吗?
-
首先,对于压力方程,因为其只有 laplacian项,所以可以推导出来这样的压力方程的系数满足 “网格单元对应的对角矩阵系数等于其余影响的单元系数之负和” 这个特点。
其次,我们来看 setReference 这个函数做了什么。查看 fvMatrix 类中 setReference 函数的实现,如下:template<class Type> void Foam::fvMatrix<Type>::setReference ( const label celli, const Type& value, const bool forceReference ) { if ((forceReference || psi_.needReference()) && celli >= 0) { source()[celli] += diag()[celli]*value; diag()[celli] += diag()[celli]; } }可以看到,这个函数确实是把对应网格的对角元素值翻倍了。 setReference 函数的目的是把指定网格(对应参数 celli)的值设置为指定的值(对应参数 value),可以为什么这样实现就可以达到这个目的呢?原理如下:
在不可压缩流体计算中,我们求解的是压力泊松方程(Pressure Poisson Equation),它通常形如:
$$ \nabla \cdot (\frac{1}{A_p} \nabla p) = \nabla \cdot (\frac{H(\mathbf{U})}{A_p}) $$
这里p是压力,A_p是速度方程离散后中心网格的系数,H(U)是一个与速度相关的项。当我们将这个方程离散化后,会得到一个大型的线性方程组:
$$ \mathbf{A} \mathbf{p} = \mathbf{b} $$
其中A是系数矩阵,p是我们要求解的、包含所有网格压力的向量,b是源项向量。关键问题:如果计算域的所有边界都是第二类边界条件(Neumann BC),比如
zeroGradient(法向梯度为零),这意味着我们只规定了压力的梯度,而没有规定压力的绝对值。从物理上讲,不可压缩流的压力是相对的。如果
p是一个有效的解,那么p + C(其中C是任意常数)也同样是一个有效的解,因为它不会改变压力的梯度(∇(p+C) = ∇p)。因此,我们必须通过指定一个点的压力值来消除这种不确定性,为整个压力场提供一个“锚点”或“基准”。
setReference的目标是强制让某个特定网格celli的压力p[celli]在求解后等于我们设定的参考值value。
也就是说,我们想让方程组的解满足:
$$ p_{\text{celli}} = \text{value} $$3. 代码实现与数学原理剖析
我们再来看这两行代码,并结合线性方程组
Ap=b在第celli行的具体形式来分析。对于网格
celli,其对应的线性方程(未修改前)是:
$$ A_{ii} p_i + \sum_{j \in N(i)} A_{ij} p_j = b_i $$
其中:i就是cellip_i是网格i的压力A_{ii}是对角线元素,对应 OpenFOAM 代码中的diag()[celli]A_{ij}是非对角线元素,表示网格i与其邻居网格j的相互影响b_i是源项,对应source()[celli]
现在我们来分析这两行代码对这个方程做了什么修改:
核心代码:
source()[celli] += diag()[celli]*value; diag()[celli] += diag()[celli];第一步:
source()[celli] += diag()[celli]*value;这行代码修改了源项
b_i。修改后的新源项b'_i为:
$$ b_i^{'} = b_i + A_{ii} \cdot \text{value} $$
此时,方程变为:
$$ A_{ii} p_i + \sum_{j \in N(i)} A_{ij} p_j = b_i + A_{ii} \cdot \text{value} $$第二步:
diag()[celli] += diag()[celli];这行代码修改了对角线元素
A_{ii}。修改后的新对角线元素A'_{ii}为:
$$ A_{ii}^{\prime} = A_{ii} + A_{ii} = 2A_{ii} $$
现在,第i行的方程最终变成了:
$$ (2A_{ii}) p_i + \sum_{j \in N(i)} A_{ij} p_j = b_i + A_{ii} \cdot \text{value} $$让我们来整理一下这个修改后的方程。我们可以把
(2A_{ii}) p_i拆开:
$$ (A_{ii} p_i + \sum_{j \in N(i)} A_{ij} p_j) + A_{ii} p_i = b_i + A_{ii} \cdot \text{value} $$也就是说,当调用了 setReference 函数后,求解的线性方程组发生了变化。通过求解这个修改后的方程,能让方程趋于收敛到 $p_i = \text{value}$ 这个解,此时
$$ A_{ii} p_i = A_{ii} \cdot \text{value} $$
因此也会使得修改前的
$$ A_{ii} p_i + \sum_{j \in N(i)} A_{ij} p_j \approx b_i $$
也同时成立。通过这样就实现了让指定的网格的解等于指定值,同时又不违反从 Laplacian 项离散后得到的方程。

