@Gengxiaotian
1.建议使用同一个box，如果距离不远
2.案例可以参考自带算例OpenFOAM-v2206\tutorials\incompressible\pimpleFoam\RAS\wingMotion
3.加密边界是根据所加密的结构外形进行外延的，具体形状和网格密度有关。如果是背景网格自然是自己设置的形状。
4.我理解refinementSurfaces更多是为了保持形状，粗糙的网格会导致几何失真。
这个参数是需要根据你的网格尺寸调整的，我看这里需要加密的网格之间间距很小，或许是这个原因。我有几个问题
1.看之前的贴图，好像区域加密也没有实现。就是refinementBox的这块代码。或许可以截取一个全景看下。
2.在refinementSurfaces里面我看到你设置了很多边界加密，为什么在refinementRegions只设置了building和tree，而且这两者似乎也没有统一。在refinementSurfaces里building是加密到2，而refinementRegions里是3-2-1.这里可能也是一个问题。
建议可以根据现在的背景网格和部分内部元素设置合理的加密模式，例如只有背景网格和tree。根据refinementBox-refinementSurfaces- refinementRegions递进式实现加密。
网格质量这一块的代码建议尝试下面这种宽松的形式试一下
meshQualityControls
{
//- Maximum non-orthogonality allowed. Set to 180 to disable.
maxNonOrtho 180;
//- Max skewness allowed. Set to <0 to disable.
maxBoundarySkewness 20;
maxInternalSkewness 4;
//- Max concaveness allowed. Is angle (in degrees) below which concavity
// is allowed. 0 is straight face, <0 would be convex face.
// Set to 180 to disable.
maxConcave 180;
//- Minimum pyramid volume. Is absolute volume of cell pyramid.
// Set to a sensible fraction of the smallest cell volume expected.
// Set to very negative number (e.g. -1E30) to disable.
minVol 1e-30;
//- Minimum quality of the tet formed by the face-centre
// and variable base point minimum decomposition triangles and
// the cell centre. Set to very negative number (e.g. -1E30) to
// disable.
// <0 = inside out tet,
// 0 = flat tet
// 1 = regular tet
minTetQuality 1e-30;
//- Minimum face area. Set to <0 to disable.
minArea -1;
//- Minimum face twist. Set to <-1 to disable. dot product of face normal
// and face centre triangles normal
minTwist -2;
//- Minimum normalised cell determinant
// 1 = hex, <= 0 = folded or flattened illegal cell
minDeterminant 1e-30;
//- minFaceWeight (0 -> 0.5)
minFaceWeight 1e-30;
//- minVolRatio (0 -> 1)
minVolRatio 1e-30;
//must be >0 for Fluent compatibility
minTriangleTwist -1;
// Advanced
//- Number of error distribution iterations
nSmoothScale 4;
//- Amount to scale back displacement at error points
errorReduction 0.75;
}
@Gengxiaotian 逐层加密可以通过refinementRegions下面的distance模式实现
@Rachel0096 这是多组分计算吗，我觉得你要检查下N2组分的初始定义，或者在程序里输出看一下是不是预想的值。我这里的问题是出现了多变量，应该不太一样。
类似这样
Info << "N2 field range: " << min(Y["N2"]).value()
<< " to " << max(Y["N2"]).value() << endl;
@yuhxFoamer
不是老师哈，我最近也在做网格验证，所以可以一起讨论下。
1.最小网格尺寸看起来变化了，网格的质量好像也不一致，看起来不是结构网格。要考虑设置相同的计算参数。
2.几何尺寸发生变化会导致雷诺数、参考面积这些的变化。我看你的计算域在三个方向上都发生了改变，检查一下基于这些几何参数的其他量是不是也相对需要改动。
你可以按照这个方案来检查，首先在原本能够顺利计算的网格上直接加密，看看是否发散。然后使用缩放命令改变网格（不再加密）transformPoints -scale "( 2 2 1)"，设置对应尺寸下的物理参数计算验证。一般来说没有很密的边界层的话可以这样调整，这样不行的话就进一步考虑离散方法和数值精度的调整，先用一阶的，再反复调整这样。
@xumengxin tensor: (0 -6.54405e-64 0 -6.54405e-64 0 -3.74512e-61 0 -3.79365e-61 0)这个矩阵几乎等于0了，一般来说普通方法都是没办法计算特征值的，需要调整精度或者忽略。如果你的程序是正确的，可以尝试修改量纲，让矩阵非奇异。
建议先贴一下网格，发一下两组网格的checkMesh，检查是否符合想象。然后检查量纲，这个发散的太严重了。
你的矩阵值太小了，尝试调整一下量纲让矩阵非奇异吧
@HITSC30 icem不是很熟练，我去试一下
@msm 我试一下哈，多谢多谢
1.我猜是symmetry这个边界条件，试一下改成wall，然后在0文件夹里自己定义上下的slip边界条件。openfoam会对生成的网格编号进行检查，外部软件的网格节点编号和blockMesh的逻辑不一样。
2.可能是前后的empty边界问题，你可以在starccm里生成3D网格后，重新在openfoam里extrude来生成前后empty边界
类似这样
constructFrom patch;
sourceCase "../w3-d_hc1-3";
sourcePatches (symFront);
// If construct from patch: patch to use for back (can be same as sourcePatch)
exposedPatchName symBack;
// Flip surface normals before usage. Valid only for extrude from surface or
// patch.
flipNormals false;
//- Linear extrusion in point-normal direction
extrudeModel linearNormal;
nLayers 1;
expansionRatio 1.0;
linearNormalCoeffs
{
thickness 1;
}
// Do front and back need to be merged? Usually only makes sense for 360
// degree wedges.
mergeFaces false; //true;
// Merge small edges. Fraction of bounding box.
mergeTol 0;
你这两个map的网格不一致，是对应不上的
@李东岳 边界层想要横平竖直，这个角上的边界层如果按照之前的做法，扩展后的最后一层特别宽，就导致它相邻的三角形网格是钝角三角形。所以希望能控制它沿着几何轮廓法向扩展，其余的部分用三角形网格填充。
@HITSC30 这里分块分不出来，请教一下方向。
@Gunther
您好，想了解切割体网格是怎样绘制的（这个网格更接近snanpy出来的网格），定向网格里没有这个选项，是通过绘制二维网格后转换的吗。
可以识别，多面体四面体都可以。paraview里关闭这个选项就可以正常显示了。
您好，我使用starccm绘制网格导入openfoam后计算会出现误差，CL值不在零轴附近波动（相同的设置计算blockMESH绘制的网格没有这个问题）。
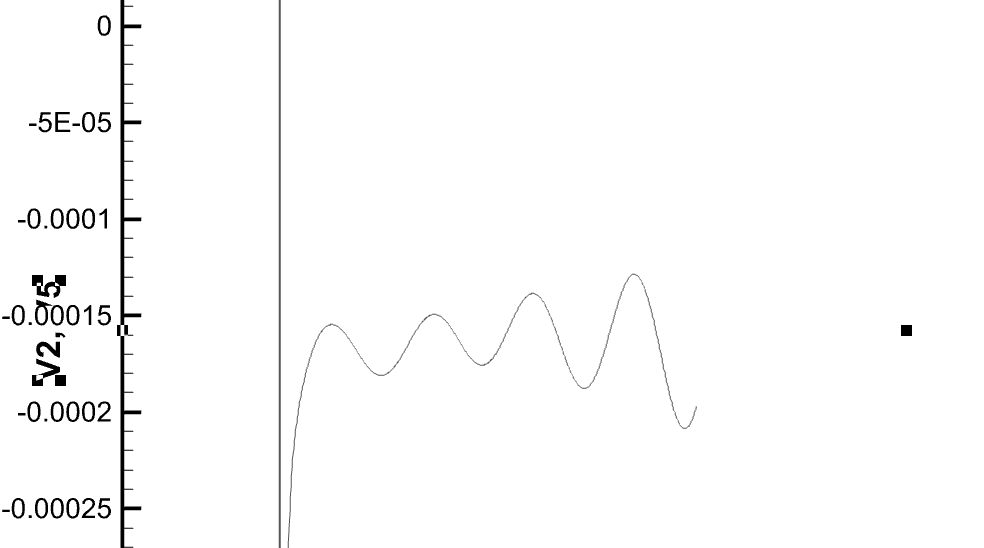
我是在starccm中通过定向网格直接绘制的三维网格，然后用ccm26ToFoam转化，想请教是什么原因。
各位老师好，
我用starccm处理边界层的时候遇到下面这个问题，尖角附近的边界层会变形，有什么办法可以自定义边界层吗。
上图是自动边界层，我希望调整成下面的边界层。
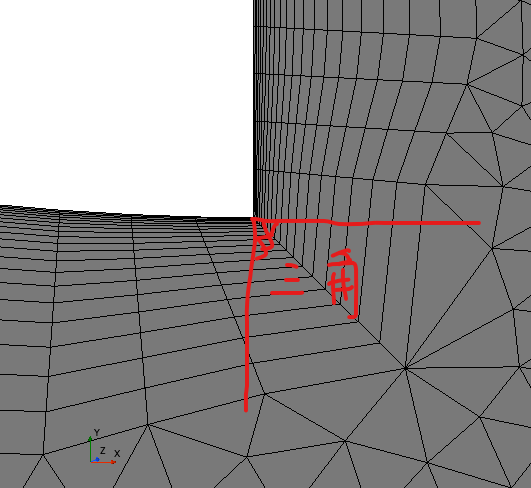
1.根据现有的结果计算一下局部库朗数，看看是否是突变的速度导致的网格变形。（尝试调整一下时间项的离散方案）
2.用比较稀疏的网格尝试计算，看看能否承受变形（去掉边界层）
3.松弛因子accelerationRelaxation 0.4;可以再调整，网格变形方式也可以尝试调整。
大概是这些方向，如果都不行。那么可以考虑使用重叠网格方案，对于刚体运动是一定可行的。
我对你这个方程不太熟悉，你自己可以对照原方程检查量纲。如果没弄错的话，
在 TEqn 方程中，fvm::ddt(T) 的维度应该是 [1 0 -3 1 0 0 0]（即温度的时间导数，单位是 K/s）。
fvm::div(phiFluid[i], T) 的维度应该是 [1 0 -3 1 0 0 0]（即对流项，单位是 K/s）。
fvm::laplacian(alphaEff, T) 的维度应该是 [1 0 -3 1 0 0 0]（即扩散项，单位是 K/s）。
rad.ST(rhoCp, T) 的维度应该是 [1 0 -3 1 0 0 0]（即辐射源项，单位是 K/s）
要让 rad.ST(rhoCp, T) 的返回值与方程中其他项的维度一致，可以检查 rad.ST 的实现或传入的参数(rhoCp)。大概是这个思路。
@xumengxin 对的，是这段时间窗口的平均值，对应的窗口值应该也有保存。