在一篇磁流体文献中看到的可压缩流方程组,和平时所见的N-S方程组求解压力和速度的方法很不一样,所以想请教一下各位老师这个方程组是确实(在某些条件下)成立还是文献给错了?
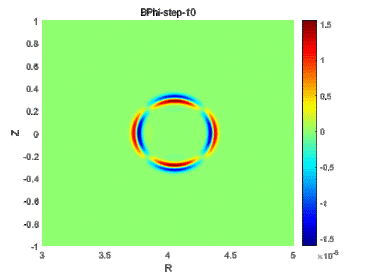
$\frac{\partial \rho}{\partial t}+\nabla \cdot (\rho v)=0$
$\frac{\partial p}{\partial t}+v \cdot \nabla p-\Gamma p \nabla \cdot v=0$
$\frac{\partial v}{\partial t}+\nabla v \cdot v-\frac{\nabla p}{\rho}-\nabla \cdot (\nu \nabla v)=0$
N
nothingts
@nothingts
帖子
-
文献中看到一个将密度压力速度列成三个方程的方程组,请教一下这个方程组与可压缩NS方程组是否矛盾 -
用有限差分做磁流体模拟但是出现了异常的震荡好像不能发动图,我试试截几个图吧(前两张是计算“正常”时,后面两张是出现了震荡和最后崩溃时的情况)
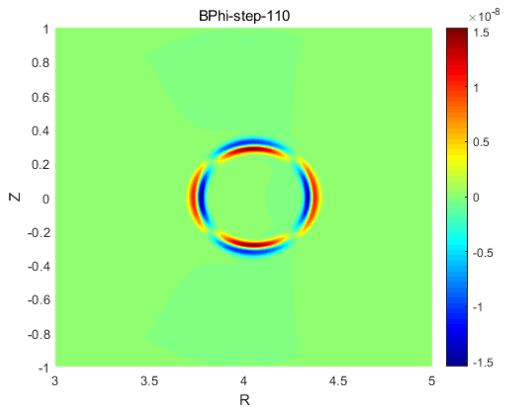
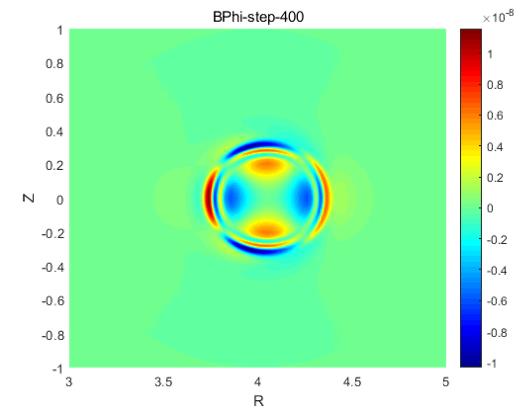
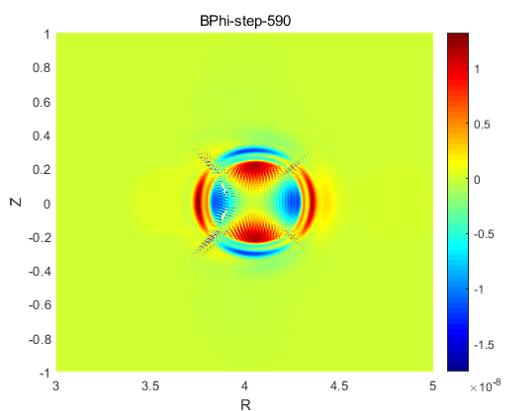
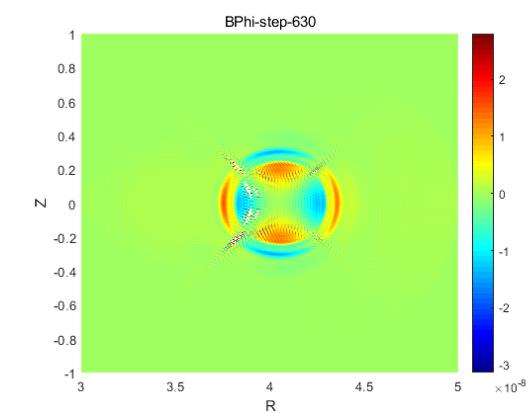
-
用有限差分做磁流体模拟但是出现了异常的震荡最近在研究用有限差分解MHD(磁流体)方程,贴一下公式:
\begin{equation}
\frac{\partial\rho}{\partial t}+\nabla\cdot\left[\left(\rho_0+\rho\right){v}\right]-\nabla\cdot\left(d\nabla\rho\right)=0\
\frac{\partial{v}}{\partial t}+\nabla{{v}}\cdot{{v}}-\frac{1}{\rho+\rho_0}\left[{j}_0\times{B}+\left(\nabla\times{B}\right)\times\left({B}+{B}_0\right)\right]-\nabla\cdot\left(\nu\nabla{v}\right)=0\
\frac{\partial{B}}{\partial t}-\nabla\times\left({v}\times{B}\right)-\eta\nabla^2{{B}}=0
\end{equation}
,时间上是一阶前差全隐求解,空间上用了二阶中心差分,尝试算了一下,在计算前期看似正常,但是后期出现了一个异常的震荡,最后导致整个计算都发散了,想请问一下这有没有可能是选取了太简单的离散格式导致了数值色散呢?