
尚佳林
帖子
-
关于含运动边界的李亚普洛夫指数场的求解疑问 -
关于含运动边界的李亚普洛夫指数场的求解疑问我用matlab写了一个有限时间的李亚普洛夫指数场(FTLE)的后处理程序,但是含有运动边界。我通过数值模拟了一个平板在水中往复运动的case,想要提取其中的拉格朗日相关结构,比如卷起的涡。于是我试图编写了李亚普洛夫指数场的求解程序,但是计算柯西格林应变张量时遇到了一些问题。我的平板存在一定厚度,平板周边有一些节点。假设初始时刻一个流体质点正好在节点处,这个节点处的速度乘以时间得到位移,与节点的坐标相加可以计算出流体质点下一个时间步的位置。但是这样计算的结果会导致平板周边处的流体质点会“流入”下个时间步平板内部。这就与壁面的边界条件相违背。强行去算会导致下图种的错误。这样的问题应当如何解决呢?
-
如何实现非结构网格求变量的梯度?其实我只是想实现tecplot里面的ddx函数,但是我找不到tecplot讨论区,所以先发这里了。
我得到的数据变量在储存在节点,而不是cell中心。网格是二维四边形网格。因为是非结构的,所以不能像笛卡尔网格那样直接求差商。我看了tecplot帮助文档里面ddx的实现方法是Moving Least-Squares,说是假定变量关于节点是二次函数,之后最小二乘法拟合出二次函数,然后将二次函数在节点的梯度近似为该变量在节点的梯度。我不明白对于二维的二次函数,tecplot是否考虑了交叉项xy?
如果不考虑的话,那我是否可以偷懒:假设需要求f的梯度,求对x的偏导的时候,完全不管y坐标。对单元的四个节点的x坐标x1,x2,x3,x4,和他们的函数值f1,f2,f3,f4进行一维的二次函数拟合。如果得到的拟合结果是f(x,y)=ax^2+bx+c,那第一个节点的x方向梯度就是把x1带入f'(x)=2ax+b中?手机打字不太方便,请见谅。
-
overset技术的后处理,如何处理两套网格交界处的数据不连续问题?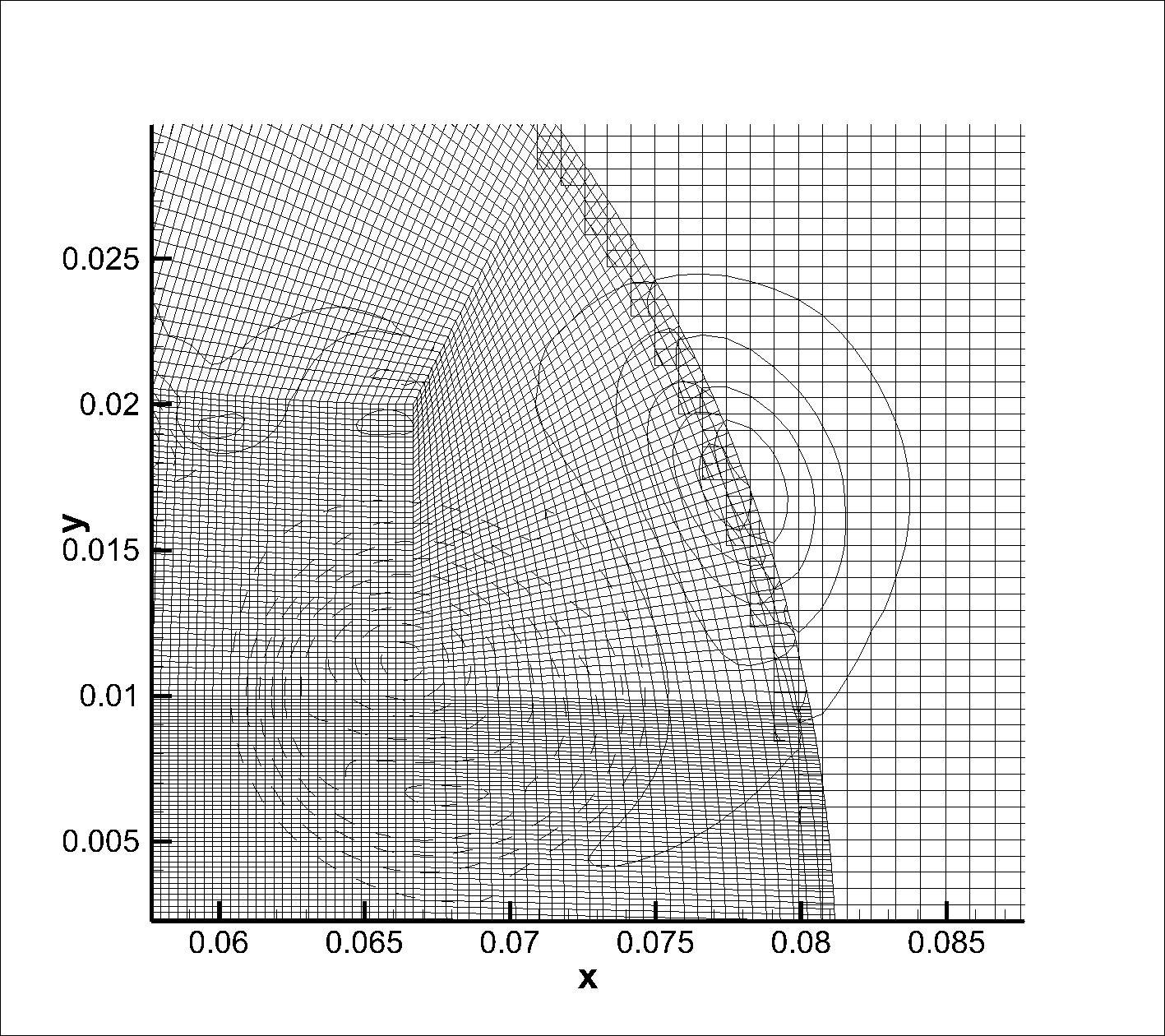
-
overset技术的后处理,如何处理两套网格交界处的数据不连续问题?关于overset后处理,已经有人发现两套网格的交界处有瑕疵了(@红豆沙 ),我也遇到了一样的问题。
我需要计算一个涡的环量,需要用速度沿涡量等值线积分。但是在两套网格的交界处,涡量等值线是断开的。那么如何将两套网格的交界区域进行处理,使得其物理量不发生太大的跃变,并且与真实的物理量误差尽量小?
我现在有一个不太好的思路,就是把交界处重叠区域的点清理掉,在交界处只保留背景网格或前景网格的点。实现方法好像可以用matlab调用convhull来形成离散点的边界。步骤就是1.导入前景网格的节点和节点数据。2.用convhull形成前景网格边界.3.导入背景网格的节点和数据。4.用射线法判断导入的背景网格点是否在前景网格范围内,如果是则删除该点。6,将过滤好的背景网格和前景网格进行重整化(不知道对于matlab画云图来说,将节点和节点数据重整化到规则区域是否必要?)然后用contour画云图。
但是这画出来的云图恐怕会在边界上产生较大的梯度。因为这是把其中一个网格的重叠区域数据去掉得到的。在边界处,物理量会从一套网格的迅速过度到另一套网格,就会出现实际物理场中不存在的梯度。有没有更好的方法和参考文献?
