UDS方程计算出来的污染物总量不守恒

[深蓝]

问题： UDS方程在封闭计算域内的计算出来的污染物总量不守恒。
详细描述：
我需要用FLUENT的UDS方程计算污染物的传播
UDS标量方法：
$$\frac { \partial \rho \phi } { \partial t } + \frac { \partial \rho U \phi} { \partial x } = \frac { \partial } { \partial x } (\Gamma _ { \Phi ,eff } \frac { \partial \phi } { \partial x } ) + S _ { 0 }$$
我在一个正方形内计算污染物的扩散，无进出口，长宽为10m* 10m，具体如图：

在计算域中间设置了UDS的源项，源的大小为0.2m*0.2m，释放时间为0.1s，代码很简单，如下：
第一种方法：

DEFINE_SOURCE(aerosol_source,c,t,dS,eqn)
{
   real x[ND_ND];
   real con, source;
   C_CENTROID(x,c,t);
  
   if(x[0]>4.5&&x[0]<5.0&&x[1]>4.5&&x[1]<5.0)
       {
        source=1;
        }
   else
       {
        source=0;
        }

   dS[eqn] = 0;
   return source;
}

第二种方法
或者Mark一个区域出来，把这个区域的source设为1，其他区域的source设为0。如图：

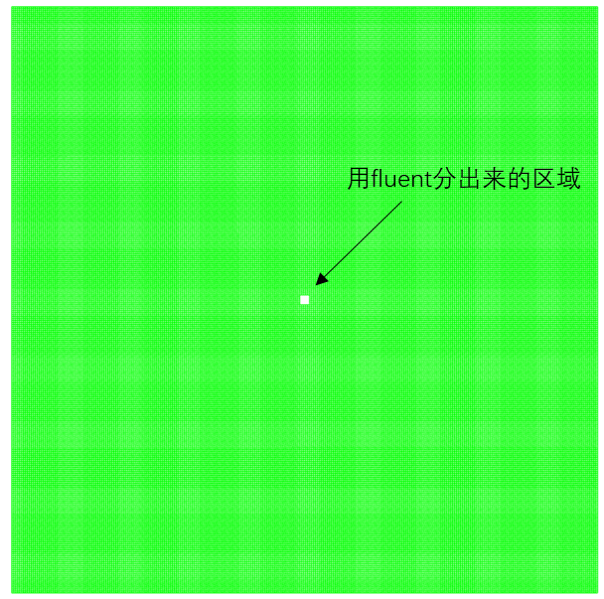
所说的守恒就是源的释放量（udf手册说DEFINE_SOURCE宏的source的单位是产生率/m3，如果是质量源就是kg/(s-m3)）乘释放时间，再乘释放体积应该等于总量，但是上述两种source设置方法得到的结果在计算域中统计都不守恒。
这两种方法计算出来结果还不同，如下：
第一种方法：


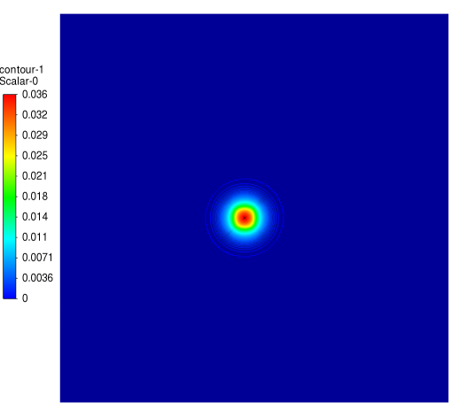
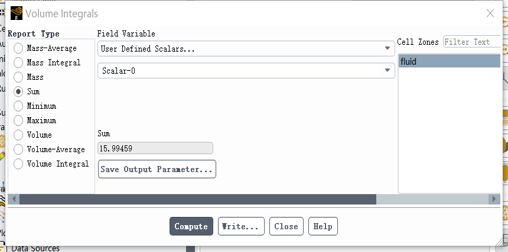
第二种方法：


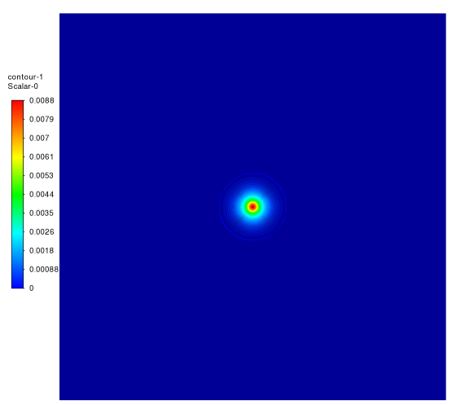
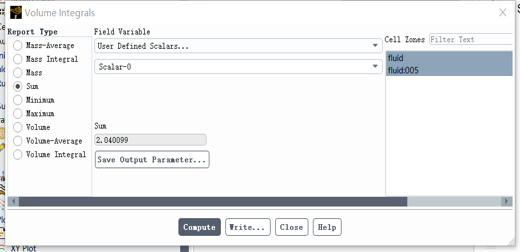
第一种方法为15.99，第二种方法为2.04。
疑问：
按理来说应该等于$0.2* 0.2*0.1=0.004$，这算出来跟释放源完全不守恒，请问大家这是什么原因呢？

[bestucan]

那个设置的值就是“值”，不是“通量”。就好比，设定一个一百度的铁球在那里，但是不是说把一百度铁球上的热量全都放到场内。

如果环境温度800度，这个100度的铁球还会吸收热量。吸收了应该升温，但是每次迭代都会又设定为100度。所以不停地吸收。

如果环境温度0度，这个100度的铁球持续释放热量。释放了应该降温，但是每次迭代都会又设定为100度，所以不停的释放。

是否吸收释放，以及吸收释放的速度取决于温度差。这里应该是浓度差。时间步越小，越能一直保持较高的浓度差，释放的就越多

就好比，给了个压力入口边界条件，却想得到固定的通量。

[深蓝]

@bestucan 谢谢您得回复，在fluent 的udf手册中写道，源项的单位是generation-rate/volume，单位体积的生成率在往外传递的时候不应该是一个通量吗？设置的“值”或是设置“通量”是否是对应的边界条件，而这个地方设置的是源项。

如果我的目的是放置一个1kg的污染物在这儿，看他随时间扩散后质量的变化情况，请问改怎么设置啊。

[bestucan]

@深蓝 可以做这样一个测试，全部区域都给这个源，看浓度是不是线性升高的就知道了是哪种了。

如果只是放置个污染源看扩散，就在计算初始化的时候设定。这样应该比较简单。
大部分计算初始化都是allzone 设定为 0 。可以在patch里分区域设定计算初始状态。
面积乘以UDS值，就是初始污染物的量。想要单位1的污染物。就给单位面积上设定uds的初始值为1。

[深蓝]

@bestucan 谢谢您得回复，通过您得建议，经过我几次尝试，结果如下：

方法一：
初始化所有区域的uds=0，u=2m/s，空气密度为1kg/m3
Patch方块的uds=1
方块的网格数量为29*29
uds的总和为 29*29*1=841
经过0.5s的发展如右图，uds的总和还是841
Note：
1、如果密度为2 kg/m3，则uds的总和为420

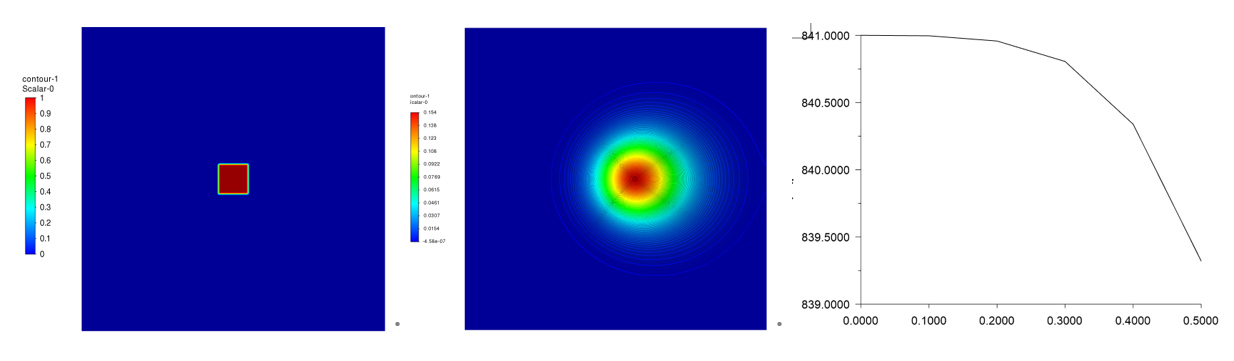
方法二：
初始化所有区域的uds=0，空气密度为1kg/m3
设置方块的source=1
方块的网格数量为29*29
进过0.5s的释放和发展如右图（线性增加），uds的总和为420
Note：
1、 如果密度为0.5 kg/m3，则uds的总和为840
2、 如果是稳态计算，uds是线性增加的


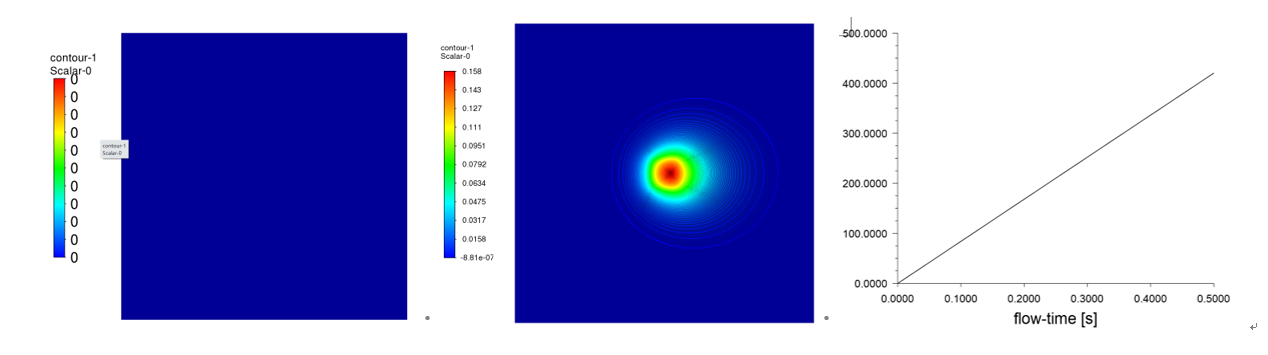
所以，source的单位应该是generation-rate*density/cell numbers

这里面需要计算网格的数量，我想udf怎么得到网格的数量呢，找了半天没有合适的，C_NNODES可以用来计算cell的节点数量，F_NNODES可以计算网格面上节点的数量，C_NFACES可以计算网格中面的数量，是否能间接得到网格的数量，但是udf手册中没有这个实例，但是在计算的时候编译一直通过不了，呜呜呜 ，代码如下：

#include "udf.h"
#include "mem.h"
DEFINE_ON_DEMAND(name)
{	
	int sum=0;
	Thread *t;
	cell_t c;	
		begin_c_loop(c, t)
			{									
			  {
			    sum+=C_NNODES(c, t);
			  }
			}
		end_c_loop(c, t)
			
	Message0("\n num=%f\n",num/4.0);
		
}

[bestucan]

@深蓝 这个网格数量……我猜应该是网格面积。这里刚好你的网格都一样大，不信你换个网格密度试试

这个材料密度，按说uds就是在场内运输个标量，跟其他的不太相关，但是一般应用中都会是某种物质，和其他物质有相互作用，然后就得有质量属性。这里材料密度能影响到uds的总量，应该是有个默认的1：1的关系，定义uds那里有个flux function，应该选的是mass flow rate。感兴趣可以找例子在udf写个flux function，兴许uds总量和材料密度的关系就没了。

这patch都解决问题了，怎么还倒腾udf

[深蓝]

@bestucan 谢谢您得持续回复。

我进行了三次尝试，200*200=40000个网格，密度=1.0时，整个计算域都添加源项，1.0s后，总量为40000，如果是300*300=90000个网格，其他不变时，总量为90000，如果密度变成2.0，总量就是45000。可见跟密度有有关系的，在UDS对流项的宏（DEFINE_UDS_FLUX）里面需要获取网格的密度，UDF手册的表述如下：

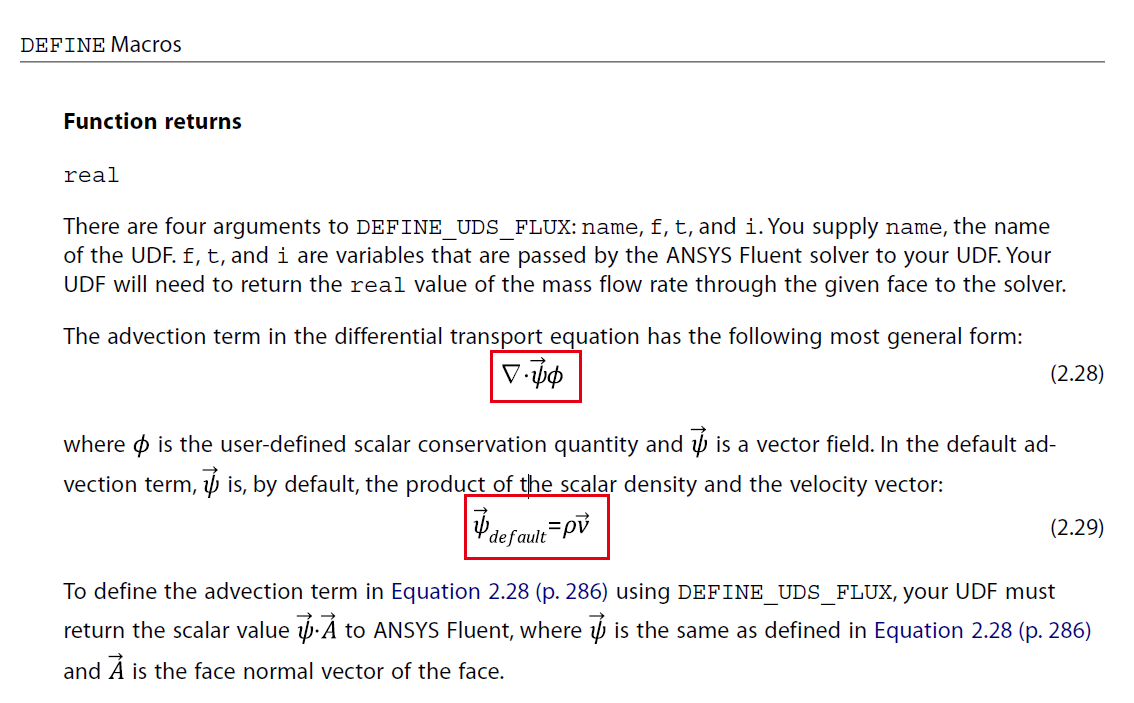
我把uds对流项中的密度都设置成1.0常数，没有效果。
我尝试把uds扩散项设置成常数也没有效果，分析应该是DEFINE_SOURCE宏返回值是一个扩散系数，密度项已经包含在默认的计算中了。
对流项代码如下：

DEFINE_UDS_FLUX(QR_flux,f,t,i)
{
    cell_t c0, c1 = -1;
    Thread *t0, *t1 = NULL;

    real NV_VEC(psi_vec), NV_VEC(A), flux = 0.0;

    c0 = F_C0(f,t);
    t0 = F_C0_THREAD(f,t);
    F_AREA(A, f, t);
	
/* If face lies at domain boundary, use face values. */
/* BOUNDARY_FACE_THREAD_P(t) expands to a function that returns TRUE if Thread *t is a boundary face thread. */

  	if(BOUNDARY_FACE_THREAD_P(t))
    	{
      		real dens;
	  
/* Depending on its BC, density may not be set on face thread. */
/* Test whether the memory for SV_DENSITY has already been allocated on a given Thread or not. */

      		if(NNULLP(THREAD_STORAGE(t,SV_DENSITY)))			
        		dens = F_R(f,t);
    		else
        		dens = C_R(c0,t0);

      		NV_DS(psi_vec,  =, F_U(f,t), F_V(f,t), F_W(f,t), *, dens);

      		flux = 1 * NV_DOT(psi_vec, A);
    	}
  
/* If face lies IN the domain, use average of adjacent cells. */
  
  	else
   		 {
      		c1 = F_C1(f,t);
      		t1 = F_C1_THREAD(f,t); 

      		NV_DS(psi_vec,  =, C_U(c0,t0),C_V(c0,t0),C_W(c0,t0),*,C_R(c0,t0));
      		NV_DS(psi_vec, +=, C_U(c1,t1),C_V(c1,t1),C_W(c1,t1),*,C_R(c1,t1));

      		flux = 1 * NV_DOT(psi_vec, A)/2.0;
    	}

  	return flux;
    
}

###另外还有个小问题想请教您一下：

问题：UDS的方程中，瞬态项和对流项的处理都有现成可用的宏，我的方程中需要添加一个四阶导数项，看来只能放在源项中，源项处理四阶导数项的话，需要自己编写四阶导数吗，源项的线性化怎么处理……，您对处理这个四阶导数项有什么建议

再次谢谢您得回复！！
尝试的代码如下：

DEFINE_SOURCE(QR_source_2d, c, t, dS, eqn)
{
	real source;
	real epsilon; 														/*stability coefficient*/
	real rho;

		
C_UDSI(c,t,1) = C_UDSI_G(c,t,0)[0];							/*DcDx, returns the x-component of the UDS gradient vector*/	
C_UDSI(c,t,2) = C_UDSI_G(c,t,1)[0];							/*DcDxx, returns the x-component of the UDS gradient vector*/	
C_UDSI(c,t,3) = C_UDSI_G(c,t,2)[0];							/*DcDxxx, returns the x-component of the UDS gradient vector*/	
C_UDSI(c,t,4) = C_UDSI_G(c,t,3)[0];							/*DcDxxxx, returns the x-component of the UDS gradient vector*/		
C_UDSI(c,t,5) = C_UDSI_G(c,t,0)[1];							/*DcDy, returns the y-component of the UDS gradient vector*/	
C_UDSI(c,t,6) = C_UDSI_G(c,t,5)[1];							/*DcDy, returns the y-component of the UDS gradient vector*/	
C_UDSI(c,t,7) = C_UDSI_G(c,t,6)[1];							/*DcDyyy, returns the y-component of the UDS gradient vector*/	
C_UDSI(c,t,8) = C_UDSI_G(c,t,7)[1];							/*DcDyyyy, returns the y-component of the UDS gradient vector*/

epsilon = 5*pow(10,-6);
rho = C_R(c,t);
source = rho * epsilon * (C_UDSI(c,t,4) + C_UDSI(c,t,8));	/*dcdxxxx+dcdyyyy*/
			
dS[eqn] = 0;												/*source linearization*/
			
return source;
					
}

[李东岳]

@深蓝 插一句，四阶导数项应该就是对$k=\nabla\cdot\nabla \phi$再做拉普拉斯：$\nabla\cdot\nabla k$

[深蓝]

@李东岳 是的，确实是这样的

[bestucan]

@深蓝 你的问题已经超出我的能力范围了
但是这里有个一个很完备的例子，应该对你有帮助。

一个简单而完整的UDS例子.zip

线性化，我能想到的方法就是泰勒级数展开了，不过要求值的变化范围不能太大，因为泰勒展开有个展开点，离展开点越近越准。这个过程应该是在软件外进行的，推出具体的计算方程再往UDF里写。

只能帮你到这了

[深蓝]

@bestucan 谢谢您的回复
我已经找到解决办法了，在fluent中通过连续用C_UDSI(c,t,0)_G的办法不可行，又找到另外一种办法，如下：

是通过计算每个cell与周围cell的“浓度差”进行计算的。但是因为fluent只能获取到一个面左右两个网格（c0，c1）的信息，所以这种方法二阶导数最高只有二阶截断误差。想要有四阶阶段误差需要有9个节点的信息（二维），fluent的udf只能获得5个节点的信息。