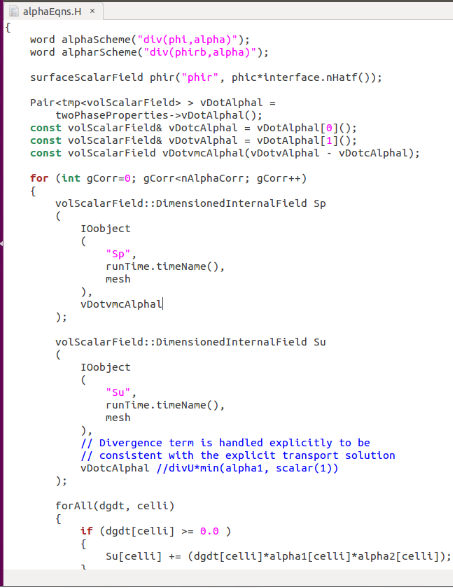
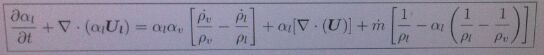{
word alphaScheme("div(phi,alpha)");
word alpharScheme("div(phirb,alpha)");
surfaceScalarField phir("phir", phic*interface.nHatf());
Pair<tmp<volScalarField> > vDotAlphal =
twoPhaseProperties->vDotAlphal();
const volScalarField& vDotcAlphal = vDotAlphal[0]();
const volScalarField& vDotvAlphal = vDotAlphal[1]();
const volScalarField vDotvmcAlphal(vDotvAlphal - vDotcAlphal);
for (int gCorr=0; gCorr<nAlphaCorr; gCorr++)
{
volScalarField::DimensionedInternalField Sp
(
IOobject
(
"Sp",
runTime.timeName(),
mesh
),
vDotvmcAlphal
);
volScalarField::DimensionedInternalField Su
(
IOobject
(
"Su",
runTime.timeName(),
mesh
),
// Divergence term is handled explicitly to be
// consistent with the explicit transport solution
vDotcAlphal //divU*min(alpha1, scalar(1))
);
forAll(dgdt, celli)
{
if (dgdt[celli] >= 0.0 )
{
Su[celli] += (dgdt[celli]*alpha1[celli]*alpha2[celli]);
}
else
{
Sp[celli] += (dgdt[celli]*alpha2[celli]);
}
if (divU[celli] >= 0.0 )
{
Su[celli] += alpha1[celli]*divU[celli];
}
else
{
Sp[celli] += divU[celli];
}
}
surfaceScalarField phiAlpha1
(
fvc::flux
(
phi,
alpha1,
alphaScheme
)
+ fvc::flux
(
-fvc::flux(-phir, alpha2, alpharScheme),
alpha1,
alpharScheme
)
);
MULES::explicitSolve
(
geometricOneField(),
alpha1,
phi,
phiAlpha1,
Sp,
Su,
1,
0
);
surfaceScalarField rho1f(fvc::interpolate(rho1));
surfaceScalarField rho2f(fvc::interpolate(rho2));
rhoPhi = phiAlpha1*(rho1f - rho2f) + phi*rho2f;
alpha1 = min(max(alpha1, scalar(0)), scalar(1));
alpha2 = scalar(1) - alpha1;
}
Info<< "Liquid phase volume fraction = "
<< alpha1.weightedAverage(mesh.V()).value()
<< " Min(" << alpha1.name() <<") = " << min(alpha1).value()
<< " Min(" << alpha2.name() <<") = " << min(alpha2).value()
<< endl;
}