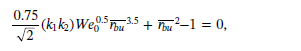如何在openfoam中求解一元高次方程
-
#include <iostream> #include "fvCFD.H" #include <stdio.h> #include <math.h> using namespace std; // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // long double f(float x){ long double f; f= 0.75/1.414*8.5*0.45*5.0 * pow(x,3) + pow(x,2) - 1.0; return f; } // Main program: int main() { long double x1,x2,x0,t,counter = 0.0; x1 = -10; x2 = 10; do{ x0=(x1+x2)/2.0; if( f(x0) * f(x1) > 0) { x1=x0; } else if (f(x0) * f(x1) < 0) { x2 = x0; } t =fabs( f(x0)); counter +=1; cout <<"Counter = "<< counter <<nl; cout <<"t = "<< t <<nl; if (counter > 100000) { break; } }while(t> 1e-5); cout<<"x0 = "<<x0<<nl; cout << " solution = " << x0<<nl; cout << "Hello World "<<nl; return 0; } // ************************************************************************* // -
或者说有没有其他的解法？
例如该方法能不能解？
该如何修改该部分code呢？？麻烦大佬指点 谢谢！
-
@东岳 是我着相了。。。我好傻，直接算就好了，干嘛搞一个class function。。。
scalar k1 = 8.5; scalar k2 = 0.45; scalar rbu_avg; scalar x0 = 0.0; scalar x2_rlarge = Dmax/2.0; scalar x1_rsmall = Dmin/2.0; scalar sat_counter = 0; scalar eps = 0.0; do { scalar x0 = (x2_rlarge + x1_rsmall) / 2.0; scalar x0_ytempavg = 0.75/sqrt(x0) * k1 *k2 * We0 * pow(x0,7.0/2.0) + pow(x0,2.0) - 1.0 ; scalar x2_ytemplarge = 0.75/sqrt(x2_rlarge) * k1 *k2 * We0 * pow(x2_rlarge,7.0/2.0) + pow(x2_rlarge,2.0) - 1.0 ; scalar x1_ytempsmall = 0.75/sqrt(x1_rsmall) * k1 *k2 * We0 * pow(x1_rsmall,7.0/2.0) + pow(x1_rsmall,2.0) - 1.0 ; if( x0_ytempavg * x1_ytempsmall > 0) { x1_rsmall=x0; } else if (x0_ytempavg * x1_ytempsmall < 0) { x2_rlarge = x0; } eps = fabs( x0_ytempavg); sat_counter +=1; if (sat_counter > 100000) { break; } }while(eps > 1e-6); rbu_avg = x0; -
@星星星星晴 老师您好，我遇到了和您一样的问题，但是我把您这段代码算下来，遇到了几个问题：
1.把这段代码放在OpenFOAM里的时候，会报错说重载的pow()模棱两可，“call of overloaded ‘pow(Foam::scalar&, Foam::scalar)’ is ambiguous”
2.我用这段代码计算一元高次方程时候总不收敛，请问您之前有这问题吗？
3.我也关注了您这篇帖子这部分内容，我看2007年的论文“A new predictive model for fragmenting and non-fragmenting binary droplet collisions”里说先把2.7次幂转换成4次幂和3次幂的两个方程，再用Runge-Kutta法进行了四次迭代，但是我没搞懂怎么用Runge-Kutta求解非微分方程，请问老师您后来尝试过用论文里的方法求解方程吗？或者对帖子里这段代码有什么改进吗？
