k-omega 模型的网格无关性验证
-
@random_ran 老师您可以给一些意见吗?
-
Sorry I had hard time to type Chinese.
Thanks for sharing this. Your finding is consistent with what I've
read this in Wilcox's book (P98).In free shear flow, k-epsilon model is unaffected by the numerical
value of $k$ and $\epsilon$, but k-omega is very sensitive to the
choice of $\omega$.But the book does not provide any suggestions on how to achieve mesh
independence on k-omega model.Speaking to mesh independence study. The idea is simple: refining the
mesh at the region with high gradient. In reality, it depends on
researchers to define where are these regions. Even in the simple
context like flow over a circular cylinder. Different people choose
different types of the computational domain, different strategies to
generate the mesh, different parameters to build the block.There are something I would investigate:
- continue refine the mesh in the "slot exit"
- expand the computational domain
- expand the "slot exit" region, especially where the shear layers
are. - use unsteady solver
- try LES if you have computational resource
Wilcox, D. C., & others, (1998). Turbulence modeling for cfd. : DCW
industries La Canada, CA. -
@random_ran 我还有一个想法。书上都说 standard k-omega 模型是一个高雷诺数模型。我图上测试的是 Re=3000 的结果,无法达到网格无关解。我另外测试了一个 Re=16500 的结果,相同的网格,居然可以达到网格无关解。
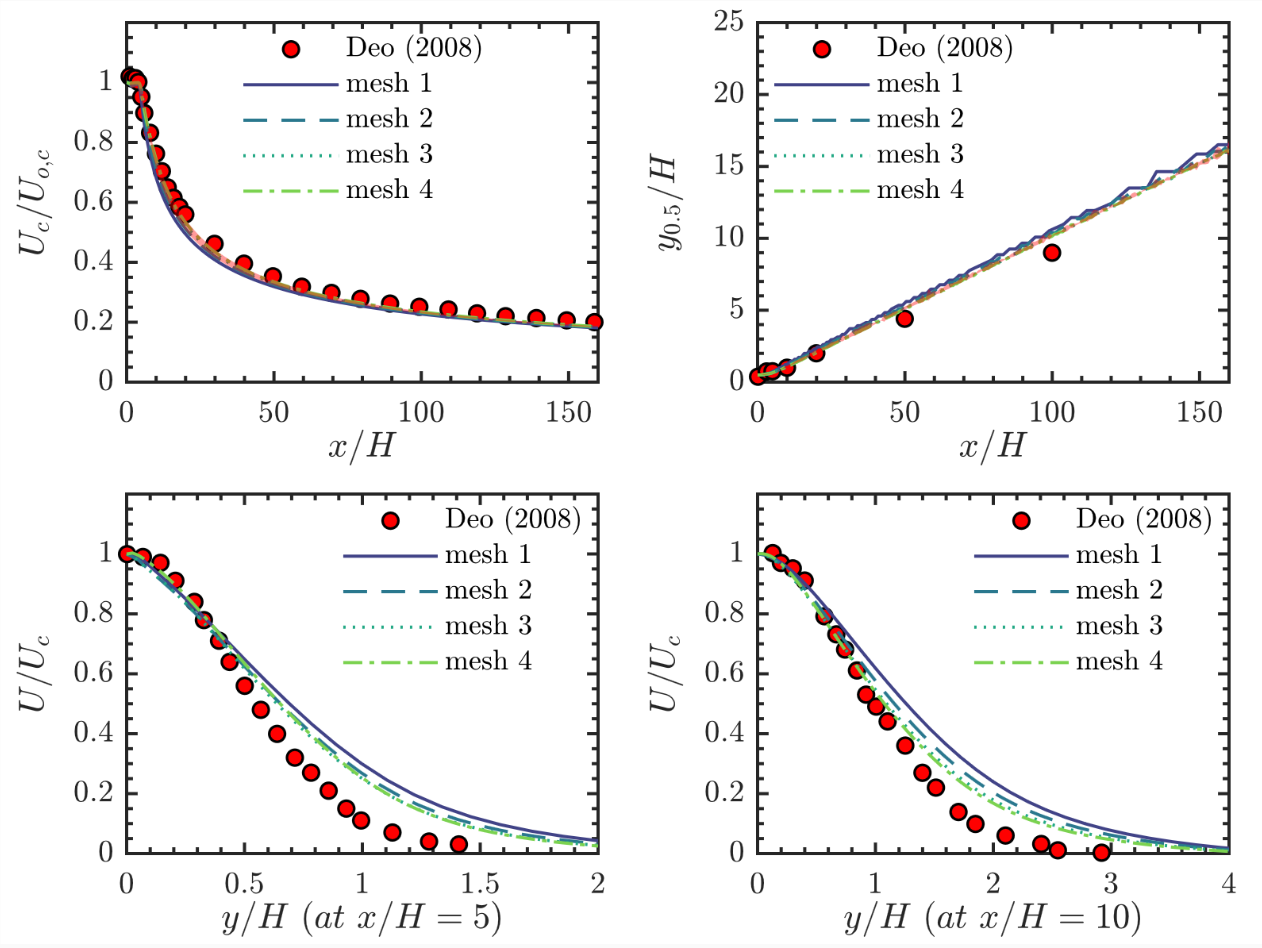
-
@random_ran 感谢老师的意见!
