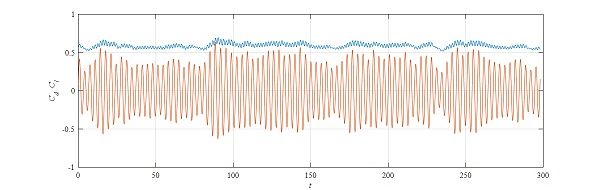
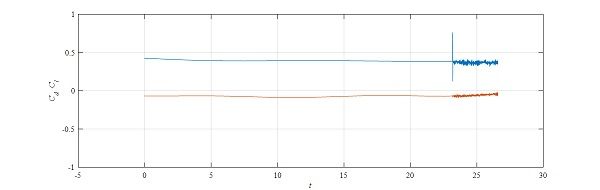
RANS 高雷诺数 圆柱绕流
-
之前一直用LES, 现在尝试RANS,有一些问题希望和大家探讨一下。
现在再算的算例基本概况:三维圆柱绕流,雷诺数15w,现在采用RNG k-epsilon模型,结构化网格质量较高。
虽然刚算了一会但是对于RANS的y+取值有一些困惑。- 网上基本上是说k-e模型的y+在30-200之间最好,要大于11。这个数值是针对的最大值,最小值,还是平均值呢?
查看了最近的时间步的y+,数值如下。可以看到最小值和最大值差的很远,最小值也是落在了粘性底层的范围内。(个人认为可能小范围的偏差不要紧,只要平均值满足即可,于是我查看了y+的分布)
Patch 2 named cylinderwalls y+ : min: 2.63471 max: 66.0352 average: 37.2911y+分布如下。来流为x+方向。可以看到分离之后大片区域是在10以下的。

一开始打算算的是5w的例子,结果发现用该湍流模型min y+很难增大到所谓的30。 于是同时调整了雷诺数和网格厚度,现在的网格首层已经达到0.01D和15w雷诺,觉得已经很粗糙了。可是y+结果还是偏差比较大。
- 采用k-e算例是会使得y+难以增大到11以上吗,还是所谓的高雷诺数指的是相当量级的值(譬如50w)?
附上现在的算例文档,有感兴趣的同学可以一起探讨下。suanli.zip
-
重新画了mesh,模型改成了sst。Re 5w
结果更奇怪了,直接算不下去。下图无量纲时间步
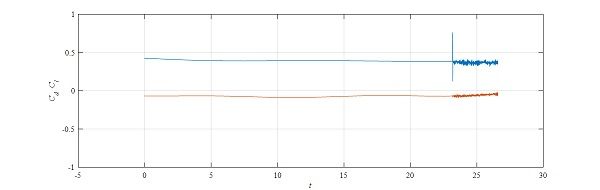
现在mesh的y+平均1.5,max 3,min0.11。应该是没什么问题,质量也很高。
上下cyclicAMI边界,圆形流域,spanwise piD。
没想到一个RANS花了这么多天还没算好。。
有大佬能帮我看看么
k
dimensions [0 2 -2 0 0 0 0]; internalField uniform 0.0021; boundaryField { front { type cyclicAMI; value uniform 0.0021; } back { type cyclicAMI; value uniform 0.0021; } inlet { type fixedValue; value uniform 0.0021; } outlet { type inletOutlet; inletValue internalField; value $internalField; } cylinderwalls { type kqRWallFunction; value uniform 0.0021; } }omega
dimensions [ 0 0 -1 0 0 0 0 ]; internalField uniform 10.9; boundaryField { cylinderwalls { type omegaWallFunction; value $internalField; } front { type cyclicAMI; } back { type cyclicAMI; } inlet { type fixedValue; value uniform 10.9; } outlet { type inletOutlet; inletValue internalField; value $internalField; } }nut
dimensions [0 2 -1 0 0 0 0]; internalField uniform 0; boundaryField { inlet { type calculated; value uniform 0; } outlet { type calculated; value uniform 0; } cylinderwalls { type nutkWallFunction; value uniform 0; } front { type cyclicAMI; } back { type cyclicAMI; } }p
dimensions [0 2 -2 0 0 0 0]; internalField uniform 0; boundaryField { front { type cyclicAMI; value uniform 0; } back { type cyclicAMI; value uniform 0; } inlet { type zeroGradient; } outlet { type fixedValue; value uniform 0; } cylinderwalls { type zeroGradient; } }U
dimensions [0 1 -1 0 0 0 0]; internalField uniform (7.5 0 0); boundaryField { front { type cyclicAMI; value uniform (7.5 0 0); } back { type cyclicAMI; value uniform (7.5 0 0); } inlet { type fixedValue; value uniform (7.5 0 0); } outlet { type zeroGradient; } cylinderwalls { type fixedValue; value uniform (0 0 0); } }fvscheme
ddtSchemes { default backward; } gradSchemes { default Gauss linear; grad(p) Gauss linear; grad(U) Gauss linear; } divSchemes { default none; div(phi,U) Gauss limitedLinearV 0.5; div(phi,k) Gauss limitedLinear 1; div(phi,omega) Gauss limitedLinear 1; div(phi,R) Gauss limitedLinear 1; div(R) Gauss linear; div(phi,B) Gauss limitedLinear 1; div(B) Gauss linear; div(phi,nuTilda) Gauss limitedLinear 1; div((nuEff*dev(T(grad(U))))) Gauss linear; } laplacianSchemes { default Gauss linear corrected; } interpolationSchemes { default linear; interpolate(U) linear; } snGradSchemes { default corrected; } fluxRequired { default no; p; Phi; }fvsolution
solvers { p { solver GAMG; tolerance 1e-04; relTol 0; smoother GaussSeidel; cacheAgglomeration true; nCellsInCoarsestLevel 200; agglomerator faceAreaPair; mergeLevels 1; } pFinal { solver GAMG; tolerance 1e-06; relTol 0; smoother GaussSeidel; cacheAgglomeration true; nCellsInCoarsestLevel 200; agglomerator faceAreaPair; mergeLevels 1; } "(U|k|nut|omega)" { solver PBiCG; preconditioner DILU; tolerance 1e-05; relTol 0; } "(U|k|nut|omega)Final" { $U; tolerance 1e-06; relTol 0; } } PIMPLE { nOuterCorrectors 3; nCorrectors 2; nNonOrthogonalCorrectors 1; pRefCell 0; pRefValue 0; }