关于绝热状态方程熵的计算过程

阿飞

OpenFOAM v2006中，adiabaticPerfectFluid状态方程如下：

$\rho (p)=\rho_{ref}(\frac{p+B}{p_{ref}+B})^{\frac{1}{n_{T}}}$

根据熵的计算公式：

$dS=c_{p}\frac{dT}{T}-(\frac{\partial v}{\partial T})_{p}dp$

求解器中将这一公式分为两部分进行积分计算，其中第一部分$c_{p}\frac{dT}{T}$ 的积分计算在thermophysicalModels/specie/thermo/hConst/hConstThermoI.H中实现，即$c_{p}*log(\frac{T}{T_{std}})$
但第二部分的积分，由于公式是绝热状态的，没有温度作为参数，想请教一下官方求解器中为什么会进行以下处理：

通过源代码公式的求导反推，官方求解器在计算第二部分积分时，在状态方程的分母上直接添加了温度T，如下式：
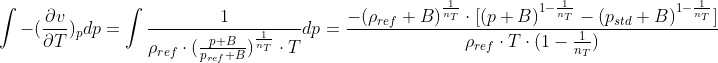
CodeCogsEqn (1).gif
公式源代码详见adiabaticPerfectFluidI.H文件的S函数：

template<class Specie>
inline Foam::scalar Foam::adiabaticperfectFluid<specie>::S 
(
    scalar p,
    scalar T
) const
{
     scalar n=1-1.0/gamma_;
     return
        -pow(p0_+B_,1.0/gamma_)*(pow((p+B_),n)-pow((Pstd+B_),n))
        /(rho0_*T*n);
}

除上述绝热状态方程外，线性变化的状态方程linear也采用了同样的处理方式，想知道为什么可以这样处理？
另外一个问题是，如果采用上述处理之后，对于气体的$c_{p}-c_{v}$，根据公式:
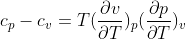CodeCogsEqn (2).gif 该如何处理？

CFD中文网

关于绝热状态方程熵的计算过程