振荡流动结果的收敛和周期问题

jinlinna

我目前模拟腔体内的自然对流，一定Ra下出现振荡流动，目前得到的流动现象都是对的，定量结果误差也很小，但是周期出现了问题，不同时间步周期表现不同。
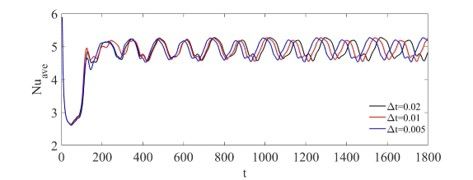
图片1.jpg
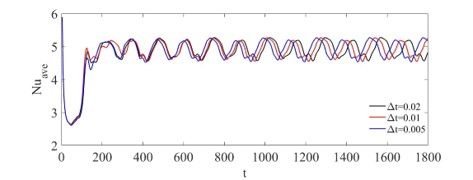
之后我换了一个简单2D模型，再次做了网格独立性检验，进一步减小时间步长，发现仅仅控制库朗数小于1无法使周期稳定下来，目前基本上库朗数到了0.02以下不同时间步长才能有固定的周期

现在我考虑是因为我的结果还没有收敛的很好，下面是采用较大时间步长的log文件截图

这个时候库朗数已经在0.2以下了，但是U、T的初始残差还是比较大，这个时候的周期比文献结果大
下面采用极小时间步长的log文件截图

这个时候库朗数是0.02以下，U、T初始残差小了很多，周期也跟文献比较接近了。

我上图中的两个时间步长残差差别比较大，但是除了周期，流动现象和定性结果差别并不大。

求助各位大佬：
1 周期振荡流动情况，残差到什么程度算是收敛的比较好？
2 在我的求解中，库朗数是不是并不重要，并不能决定我的时间步长的选取？还是因为我的求解设置问题导致目前库朗数极小才能得到正确的周期

jinlinna

我目前的求解器是在pisoFoam基础上改的，下面是我的fvschemes和fvsolution

ddtSchemes
{
    default         CrankNicolson 0.9;
}

gradSchemes
{
    default         Gauss linear;
}

divSchemes
{
    default         none;
    div(phi,U)      Gauss linearUpwind grad(U);
    div(phi,T)      Gauss limitedLinear 1;
}

laplacianSchemes
{
    default         Gauss linear uncorrected;
}

interpolationSchemes
{
    default         linear;
}

snGradSchemes
{
    default         uncorrected;
}

solvers
{
    p
    {
        solver          GAMG;
        smoother        DIC;
        tolerance       1e-6;
        relTol          0.05;
    }
    
    pFinal
    {
        $p;
        relTol          0;
    }

    "(U|T)"
    {
        solver           PBiCGStab;
        preconditioner   DILU;
        tolerance        1e-8;
        relTol           0.1;
    }

    "(U|T)Final"
    {
        $T;
        relTol          0;
    }
}

PISO
{
    nCorrectors     3;
    nNonOrthogonalCorrectors 1;
    pRefCell        0;
    pRefValue       0;
}

relaxationFactors
{
    equations
    {
        ".*"   1;
    }
}

李东岳

@jinlinna 你这个网格质量很差么？我看你加了压力修正。

jinlinna

@李东岳网格质量应该还可以，都是正交网格，您说的是这里吗

nNonOrthogonalCorrectors 1;

这个我是之前的网格用的没有改

jinlinna

@李东岳老师，我的网格都是这种比较规则的正交网格，网格做过独立性检验了
图.png

李东岳

@jinlinna

目前得到的流动现象都是对的，定量结果误差也很小，但是周期出现了问题，不同时间步周期表现不同。

仅仅是这个问题？这个问题可以理解。你下面这个图看起来比较明显。如果你单独对比周期，应该不会差这么多。

替代文字

压力不需要非正交修正

jinlinna

@李东岳谢谢李老师！我算了一下周期在库朗数小于0.1以后的误差基本非常笑了，而且试的时候发现nCorrectors的设置对不同时间步得到周期值影响比较大。

还有一个问题是：从我的log文件里面看到初始残差一直都比较大，库朗数在0.15的时候，Ux的初始残差一直在2e-3的左右下不去，T的初始残差也在1e-4。我减小时间步到库朗数到0.018的时候，Ux的初始残差降到2e-4左右，T的初始残差降到1e-5左右。

想问一下您这种周期震荡流动，OF里面的初始残差到多少是比较好的结果？我上面采用的两种时间步的平均结果误差在1%，有没有必要像上面一样减小时间步让速度的初始残差降到比较低的位置？

李东岳

@jinlinna 没必要，瞬态算例残差就是不太好降

jinlinna

@李东岳好的李老师，我明白了，特别感谢您！！

CFD中文网

振荡流动结果的收敛和周期问题