3阶以上矩阵定义与求逆

[lizhisongsjtu]

做2个算法植入，求解非线性方程组，需要构造Jacobian矩阵并求其逆矩阵。

算法1中，矩阵为3阶方阵，类型为复数张量Tensor<complex>，可正常调用函数inv计算逆矩阵。
算法2中，矩阵为8阶方阵，按常规的C++语法complex JacobianM定义矩阵，调用求逆函数时报错，求逆函数不适用C++语法定义的矩阵求逆。

对上述矩阵求逆，请教道友如何定义一个3阶以上矩阵：
（1）可求逆
（2）逆矩阵可与向量点乘，&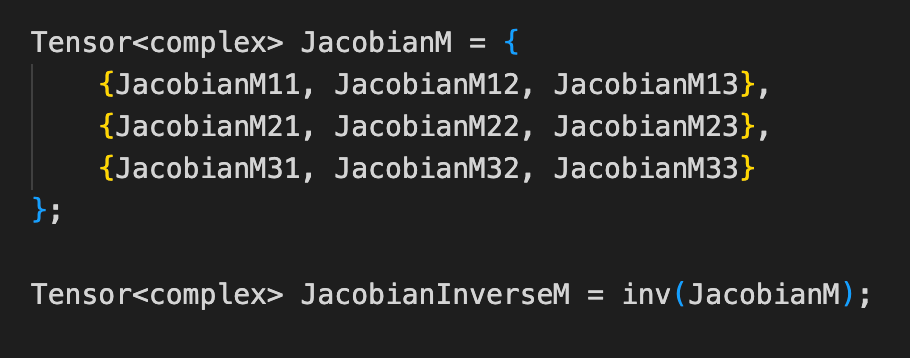

算法1的OpenFOAM脚本，成功运行。

算法2的Python脚本，验证准确。

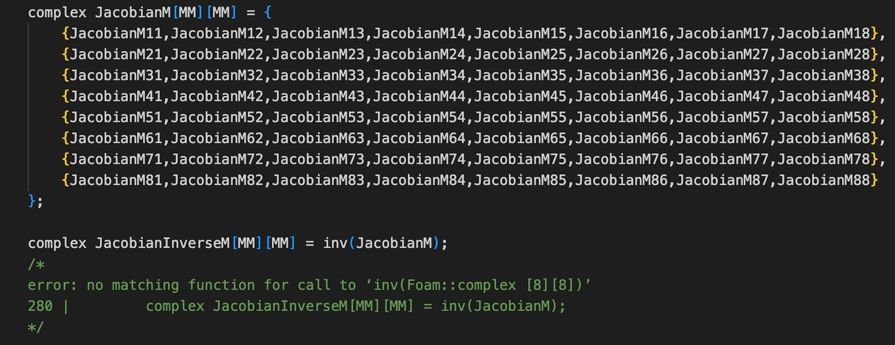算法2的OpenFOAM脚本，报错。

[李东岳]

如何定义一个3阶以上矩阵：

SquareMatrix<scalar> hmm(3);

    hmm(0, 0) = -3.0;
    hmm(0, 1) = 10.0;
    hmm(0, 2) = -4.0;
    hmm(1, 0) = 2.0;
    hmm(1, 1) = 3.0;
    hmm(1, 2) = 10.0;
    hmm(2, 0) = 2.0;
    hmm(2, 1) = 6.0;
    hmm(2, 2) = 1.0;

Info<< inv(hmm);

类似这样可以么

[lizhisongsjtu]

openFoam中实现非线性方程组求解中的Jacobian矩阵、求逆、矩阵与列向量相乘

谢谢东岳回复。今天试了一下，SquareMatrix类型的方阵，无法求逆。

此外，还需要一个向量与方阵相乘的列向量，列向量的定义用List定义，不能点乘。

(牛顿法求非线性方程组)

#include "fvCFD.H"

// #include "complex.H"

#include "SquareMatrix.H"


int main(int argc, char *argv[])
{
    Info << "Operation of Tensor and Square Matrix in OpenFOAM:" << endl;

 
    Info << endl << endl << "Part I: tensor" << endl;
    tensor myTensor(.1, 1, 2, 3, 4, 5, 6, 7, 8);
    vector myVector(1, 1, 1.);

    Info << "myTensor = " << myTensor << endl;
    Info << "myTensorInverse = " << inv(myTensor) << endl;
    Info << "det(myTensor) = " << det(myTensor) << endl;
    Info << "tr(myTensor) = " << tr(myTensor) << endl;
    Info << "myTensor & myVector = " << (myTensor & myVector) << endl;



    Info << endl << endl << "Part II: SquareMatrix" << endl;

    // 目标矩阵是8x8，暂时用4x4替代。
    const label M(4);
    // 创建一个List
    List<scalar> myList(M);
    myList[0] = 1;
    myList[1] = 1;
    myList[2] = 1;
    myList[3] = 1;

    // 创建方阵并赋值。
    SquareMatrix<scalar> hmm(M);

    hmm(0, 0) = -3.0;
    hmm(0, 1) = 10.0;
    hmm(0, 2) = -4.0;
    hmm(0, 3) = -5.0;

    hmm(1, 0) = 2.0;
    hmm(1, 1) = 3.0;
    hmm(1, 2) = 10.0;
    hmm(1, 3) = 9.0;
    
    hmm(2, 0) = 2.0;
    hmm(2, 1) = 6.0;
    hmm(2, 2) = 1.0;
    hmm(2, 3) = 5.0;

    hmm(3, 0) = 5.0;
    hmm(3, 1) = 8.0;
    hmm(3, 2) = 10.0;
    hmm(3, 3) = -4.0;



    Info << "det(hmm) = " << det(hmm) << endl;
    Info << "hmm.size() = " << hmm.size() << endl;

    // Info << "tr(hmm) = " << tr(hmm) << endl;
    // Info << "inv(hmm) = " << inv(hmm) << endl;

    // Info << "hmm & myList = " << (hmm & myList) << endl;



    return 0;
}

[李东岳]

我试了一下，下面可以求逆，可以改成n阶

scalarSquareMatrix M(3, Zero);
M(0, 0) = 4;
M(0, 1) = 12;
M(0, 2) = -16;
M(1, 0) = 12;
M(1, 1) = 37;
M(1, 2) = -43;
M(2, 0) = -16;
M(2, 1) = -43;
M(2, 2) = 98;
LUscalarMatrix L(M);

scalarSquareMatrix invM(3);
L.inv(invM);

下面可以实现点乘：

scalarSquareMatrix M(3, Zero);
M(0, 0) = 4;
M(0, 1) = 12;
M(0, 2) = -16;
M(1, 0) = 12;
M(1, 1) = 37;
M(1, 2) = -43;
M(2, 0) = -16;
M(2, 1) = -43;
M(2, 2) = 98;

scalarField x(3, Zero);
scalarField Mx = M*x;

汇总一下

scalarSquareMatrix squareMatrix(3, Zero);
squareMatrix(0, 0) = 4;
squareMatrix(0, 1) = 12;
squareMatrix(0, 2) = -16;
squareMatrix(1, 0) = 12;
squareMatrix(1, 1) = 37;
squareMatrix(1, 2) = -43;
squareMatrix(2, 0) = -16;
squareMatrix(2, 1) = -43;
squareMatrix(2, 2) = 98;
const scalarField S(3, 1);

LUscalarMatrix L(squareMatrix);

scalarSquareMatrix inv(3); //矩阵求逆
L.inv(inv);

scalarField x(3, Zero);
scalarField Mx = squareMatrix*x; //矩阵乘以向量

scalarField x(L.solve(S)); //计算L \cdot x = S

[lizhisongsjtu]

@李东岳 在实数域内，这个方法完全可行。

可惜，我构建的矩阵类型是复数，上述方法暂时不支持扩展到复数域。

参考了CFD-online上帖子的回复，采用QR分解，把待分解的矩阵创建为RectangularMatrix<complex>类型。

创建QRMatrix<complex> 类型的矩阵，需要提供至少两个参数。
参考QRMatrix构造函数

//- Construct with a matrix and perform QR decomposition
        explicit QRMatrix
        (
            const modes mode,
            const outputs output,
            const bool pivoting,
            MatrixType& A
        );
 
        //- Construct with a const matrix and perform QR decomposition
        explicit QRMatrix
        (
            const MatrixType& A,
            const modes mode,
            const outputs output = outputs::BOTH_QR,
            const bool pivoting = false
        );

用如下语句创建QR矩阵，报错。

RectangularMatrix<complex> JacobianM_QR({3,3}, Zero);
    JacobianM_QR(0, 0) = 4;
    JacobianM_QR(0, 1) = 12;
    JacobianM_QR(0, 2) = -16;
    JacobianM_QR(1, 0) = 12;
    JacobianM_QR(1, 1) = 37;
    JacobianM_QR(1, 2) = -43;
    JacobianM_QR(2, 0) = -16;
    JacobianM_QR(2, 1) = -43;
    JacobianM_QR(2, 2) = 98;

    Info << "JacobianM_QR = " << JacobianM_QR << endl;
    Info << "JacobianM_QR.size() = " << JacobianM_QR.size() << endl;

    // QRMatrix<complex>  QRM(JacobianM_A);
    // QRMatrix<complex>  QRM(JacobianM_A, uint8_t(1));
    QRMatrix<complex>  QRM(JacobianM_A, (uint8_t)1);

  // QRMatrix<complex>  QRM(JacobianM_QR, *);
  // *位置是uint8_t类型的1，

[lizhisongsjtu]

下面的语句可以了

    QRMatrix<RectangularMatrix<complex>> QRM
    (
        JacobianM_QR,
        QRMatrix<RectangularMatrix<complex>>::modes::ECONOMY,
        QRMatrix<RectangularMatrix<complex>>::outputs::ONLY_R
    );

[李东岳]

[lizhisongsjtu]

总结一下:

求任意矩阵的逆矩阵，OpenFOAM中有三种方法:

(1) LU-scalarSquareMatrix，实数、方阵；

(2) QR-RectangularMatrix<Type> or SquareMatrix<Type> ，实数/复数、方阵/非方阵；

(3) SVD-scalarRectangularMatrix，实数、方阵/非方阵。

[李东岳]

绝对到位！嘎嘎一嘎子！