icoFoam学习的几个问题
-
各位老师好,
最近在学习icoFoam,参考李老师写的 CFD:不可压+瞬态算法,有几个问题没有弄清楚,发出来向大家请教。
我按照原生的cavity案例运行,为了计算方便修改成四个网格,并且把边界条件都去掉了。
dimensions [0 1 -1 0 0 0 0]; internalField nonuniform List<vector> 4((1 0 0)(1 0 0)(2 0 0)(2 0 0)); boundaryField { movingWall { type noSlip; } fixedWalls { type noSlip; } frontAndBack { type empty; } }主要希望方便计算系数.但是这里就有一个问题,我直接定义了四个网格的速度,我原本以为速度应该处于网格中心,结果看起来处于上下边界。所以直接把所有网格的速度都改为1了,如下图。
根据理论推导的离散结果,可以写出系数矩阵A
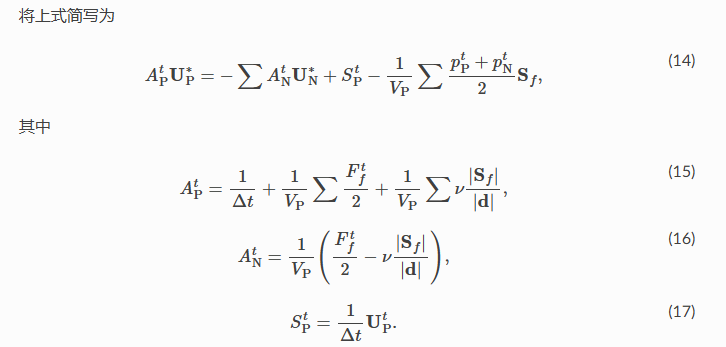
这里我输出没有计算之前的矩阵,是一个对角占优的阵,形式应该没问题=== Matrix CoeffMat before adding contribution of BCs === 0.0056 -0.0001 -0.0001 0 -0.0001 0.0056 0 -0.0001 -0.0001 0 0.0056 -0.0001 0 -0.0001 -0.0001 0.0056根据上面的公式非对角的元素可以按照位置计算,比如A10(第二行第一列)

完全没对上,不知道哪里有问题,请大家帮忙看下。
-
@ice_flow 在 icoFoam学习的几个问题 中说:
这里我输出没有计算之前的矩阵,是一个对角占优的阵,形式应该没问题
这个是用什么代码输出的,是D还是A。你最好把矩阵的全部系数输出出来,例如:
//Info<< "diag(): " << UEqn.diag() << endl; //Info<< "upper(): " << UEqn.upper() << endl; //Info<< "lower(): " << UEqn.lower() << endl; //Info<< "source(): " << UEqn.source() << endl; //Info<< "upperAddr(): " << UEqn.lduAddr().upperAddr() << endl; //Info<< "lowerAddr(): " << UEqn.lduAddr().lowerAddr() << endl; //Info<< "internalCoeffs():" << UEqn.internalCoeffs() << endl; //Info<< "boundaryCoeffs():" << UEqn.boundaryCoeffs() << endl; //Info<< "D(): " << UEqn.D() << endl; //Info<< "UEqn(): " << UEqn << nl;你那个矩阵去掉边界条件影响没有。
你最好一项一项debug,先把扩散项(粘度为0)去掉,然后用中心格式,然后用稳态。先单单看对流项的。然后再看对流+扩散项的。然后加上时间项。
然后把你的计算域每个网格改成
1*1, 而不是0.1*0.1,都可以方便你debug然后最好能减去边界条件的影响,我看你那面有noslip。我没有尝试过xyz全部都是empty可不可以。另一个就是做1D的网格,你可以做3-5个网格,左边固定进口速度1,右边零法向梯度。
-
谢谢老师,我重新调整了案例,麻烦再帮我看一下。
绘制四网格一维模型,并且设置左侧入口速度为1,右侧出口零梯度。
边界条件设置如下
U
dimensions [0 1 -1 0 0 0 0]; internalField uniform (1 0 0); boundaryField { inlet { type fixedValue; value $internalField; } outlet { type zeroGradient; } frontAndBack { type empty; } Walls { type zeroGradient; } }P
dimensions [0 2 -2 0 0 0 0]; internalField uniform 0; boundaryField { inlet { type zeroGradient; } outlet { type zeroGradient; } frontAndBack { type empty; } Walls { type zeroGradient; } }设置对流项的离散为中心差分格式,也叫线性格式
divSchemes { default none; div(phi,U) Gauss linear; }修改动量方程,只保留对流项,并输出各项矩阵系数
// Momentum predictor fvVectorMatrix UEqn ( //fvm::ddt(U) fvm::div(phi, U) //- fvm::laplacian(nu, U) ); fvVectorMatrix UEqnWithPressure(UEqn == -fvc::grad(p)); if (piso.momentumPredictor()) { solve(UEqnWithPressure); } labelUList lAdd = UEqnWithPressure.lduAddr().lowerAddr(); labelUList uAdd = UEqnWithPressure.lduAddr().upperAddr(); labelUList oAdd = UEqnWithPressure.lduAddr().ownerStartAddr(); scalarField lower = UEqnWithPressure.lower(); scalarField upper = UEqnWithPressure.upper(); scalarField diag = UEqnWithPressure.diag(); vectorField source = UEqnWithPressure.source(); Info << "lowerAddr:" << lAdd << nl << endl; Info << "upperAddr:" << uAdd << nl << endl; Info << "ownerStartAddr:" << nl << oAdd << nl << endl; Info << "lower:" << lower << nl << endl; Info << "upper:" << upper << nl << endl; Info << "diag:" << nl << diag << nl << endl; Info << "source:" << nl << source << nl << endl; //Info << UEqn << endl;输出结果如下
Starting time loop Time = 0.001 Courant Number mean: 0.001 max: 0.001 smoothSolver: Solving for Ux, Initial residual = 0, Final residual = 0, No Iterations 0 smoothSolver: Solving for Uy, Initial residual = 0, Final residual = 0, No Iterations 0 lowerAddr:3(0 1 2) upperAddr:3(1 2 3) ownerStartAddr: 5(0 1 2 3 3) lower:3{-0.5} upper:3{0.5} diag: 4(0.5 0 0 -0.5) source: 4{(0 0 0)} === Matrix CoeffMat before adding contribution of BCs === 0.5 0.5 0 0 0 -0.5 0 0.5 0 0 0 -0.5 0 0.5 0 0 0 -0.5 -0.5 0 === Matrix CoeffMat after adding contribution of BCs === 0.5 0.5 0 0 1 -0.5 0 0.5 0 0 0 -0.5 0 0.5 0 0 0 -0.5 0.5 0可以看到,系数矩阵并不是一个对角占优的矩阵,所以无法推进(个人看法)
进一步按照理论计算矩阵内的各项系数:
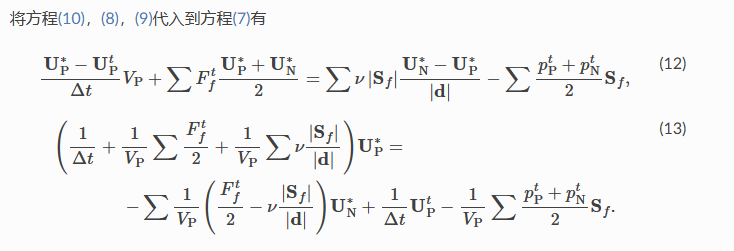
由于修改后的方程只含有对流项,所以离散结果可以进一步简化:
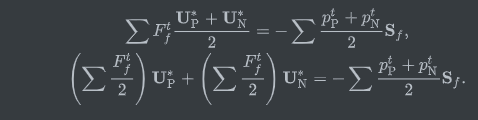
计算A10如下:
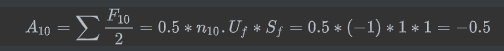
看起来没有问题,但是根据边界条件,只有入口边界的速度为1,如下图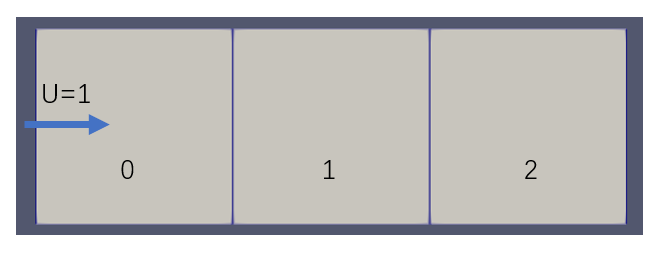
所以
 ,按照这样计算的$A_{10}$应该是 -0.25,和输出的矩阵系数也不一样。
,按照这样计算的$A_{10}$应该是 -0.25,和输出的矩阵系数也不一样。进一步的,计算对角矩阵系数(其实和次对角一样),怎么会有0出现,请老师帮忙解惑。


