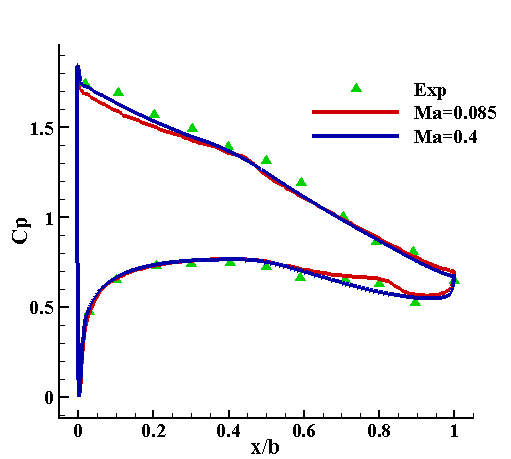
rhoSimpleFoam 求解可压缩流动时一个奇怪的现象
-
@paopaoai11
非常感谢您指出我的一些错误,受教了。我再结合您的回答说一下我的理解哈。
第一点是前缘滞止所造成的顺压梯度只是一个流动加速的有利因素。
第二点是流体在前缘加速,动压升高,静压降低,确实是对应一个膨胀过程,说压缩确实不合适。
第三点是曲率对流动的影响,我当时的理解是受到前缘壁面的扰动,局部存在一个收缩的过程,也就对应曲率的影响。 -
@paopaoai11
另外,关于前缘流动的压缩,这个是指的流体虚拟流道的面积被压缩,因而流体流速增加,压强降低,密度增大。 -
@paopaoai11 另外,关于前缘流动的压缩,这个是指的流体虚拟流道的面积被压缩,因而流体流速增加,压强降低,密度减小,(比体积增大
 )
) -
@paopaoai11 为什么曲率越大,流速越大?或者说为什么曲率越大,压力越小?
-
@宝丁 我明白你的意思,你是把叶片表面和主流间假想了一个流道,然后来解释这种现象。但这是不正确的,这也是很多同学常犯的理解上的错误。下面我举一个例子来说明一下。
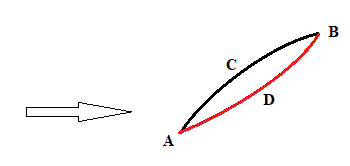
在均匀流场中放置一段曲线壁面,如下图所示,一种是ACB形式的上凸壁面,一种是ADB形式的下凹壁面,两者首尾端点位置相同,我们来考察在这两种情况下B点处的流动。试想一下,如果“假想流道”理论成立的话,由于B点位置一样,那么B点处速度应该相同才对,但事实上ACB所对应的B处的速度要远高于ADB所对应的B处的速度。所以,这种“假想流道”或“虚拟流道”理论是不对的。
-
@paopaoai11
首先,目前咱们共同的观点在于吸力面近前缘处局部加速主要是由该处流线曲率决定的,而不同的观点在于曲率导致前缘加速现象的机理是什么。
我的观点在于曲率的存在使得来流虚拟流道被压缩,因而流动流速增加。这里对虚拟流道加以解释:壁面的存在使得流场中产生了相应的扰动,不同壁面所对应的扰动传播的距离是不同的,因此将壁面至扰动传播的边界称之为虚拟流道,其是变化的,而非一成不变的。目前这个观点的问题在于我还没有定量的去描述这个虚拟流道,但就流动细节,这又是客观存在的。
但是凹凸曲面的虚拟边界相同吗?用凹凸曲面举例只是对为什么前缘加速只在吸力面一侧显著的复述罢了。注意,这并不是说压力面一侧没有。
其次,我不同意你的这一观点:
叶栅前缘吸力面局部加速跟流动滞止没太大关系,因为前缘滞止点压力最大也不会超过气流总压,所以由顺压梯度造成的加速最大也不会超过主流速度。
这个观点暗含了一个条件:流场中静压处处小于进口静压,但是这并不现实。在本问题中,叶栅前缘的最小静压可是要比进口静压小很多,因而并不一定能保证顺压梯度造成的加速最大也不会超过主流速度。
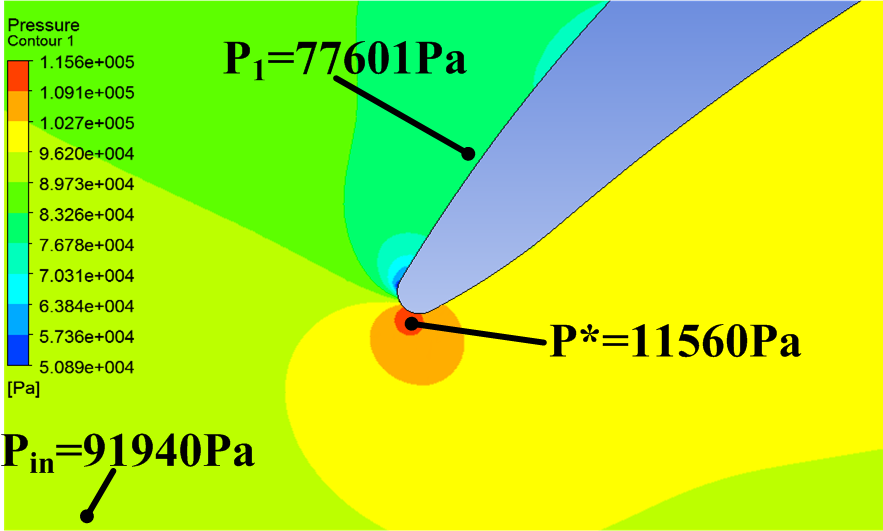
此外,关于前缘加速的原因我想通过圆柱扰流的算例加以说明:
下图给出了圆柱扰流瞬态静压与速度云图,流体首先在圆柱前缘滞止,静压升高,而在尾迹区,分离涡的存在使得该处为一个低压区,因此在圆柱上下表面存在一个较大的静压梯度,气流加速。
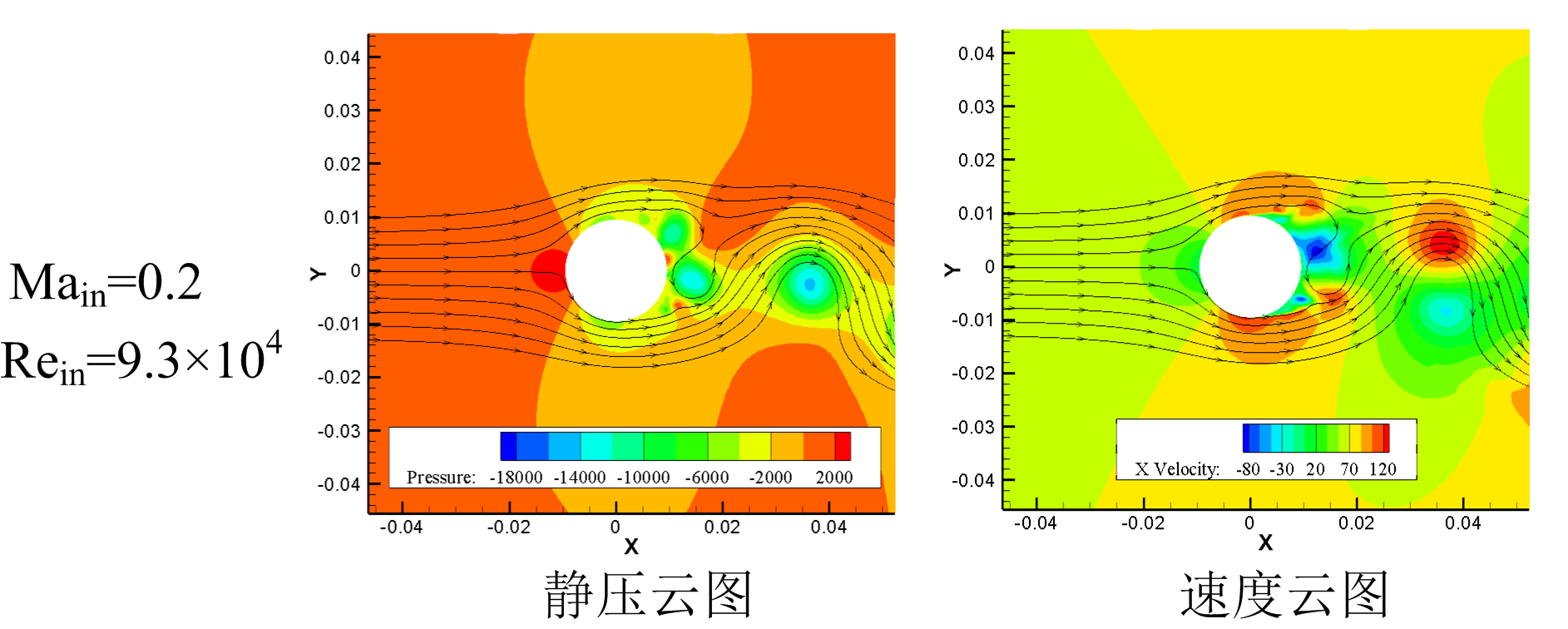
综上所述,曲率的存在使得来流虚拟流道被压缩,流体流速增加,其动力来源是静压差。