网格与圆管层流

winsway_zero

这里已经解决了，虽然用的方法精度不是很高，但是非正交修正还是很重要的。梯度计算和扩散项的延迟修正对于计算有很大影响。
1.网格是柱坐标，不采用非正交修正：

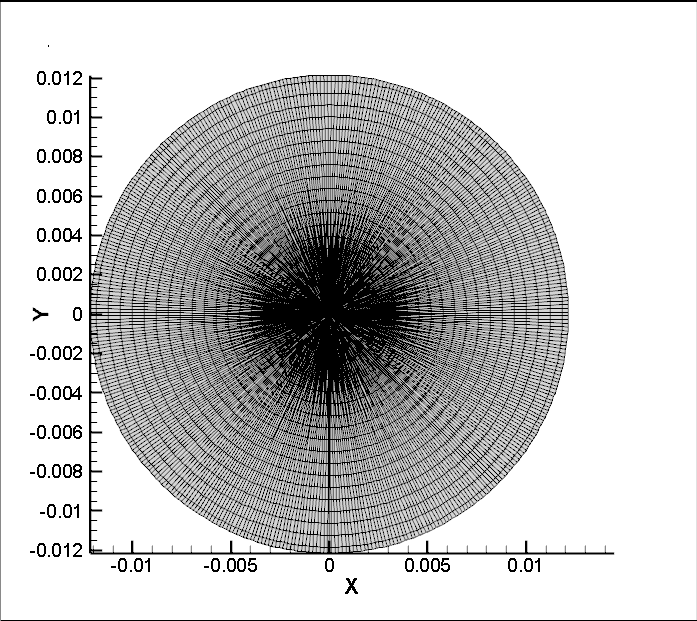
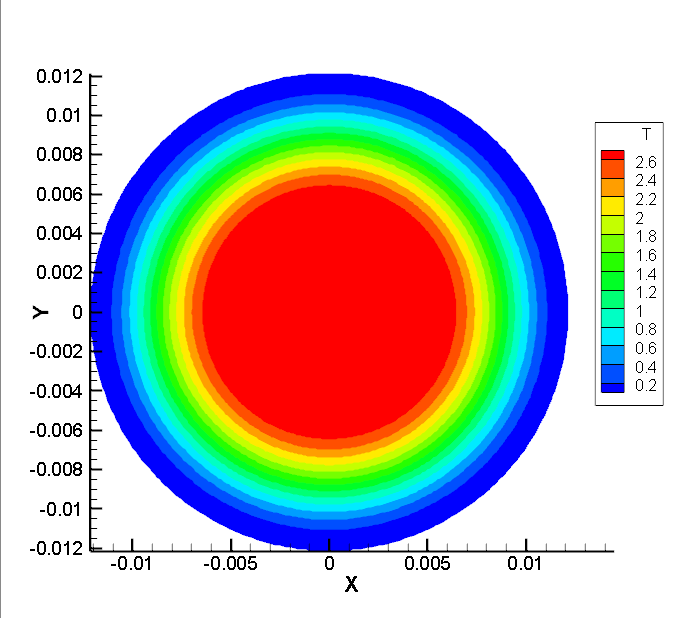
可以看出速度场是不对的。
2.网格非正交，不采用非正交修正：

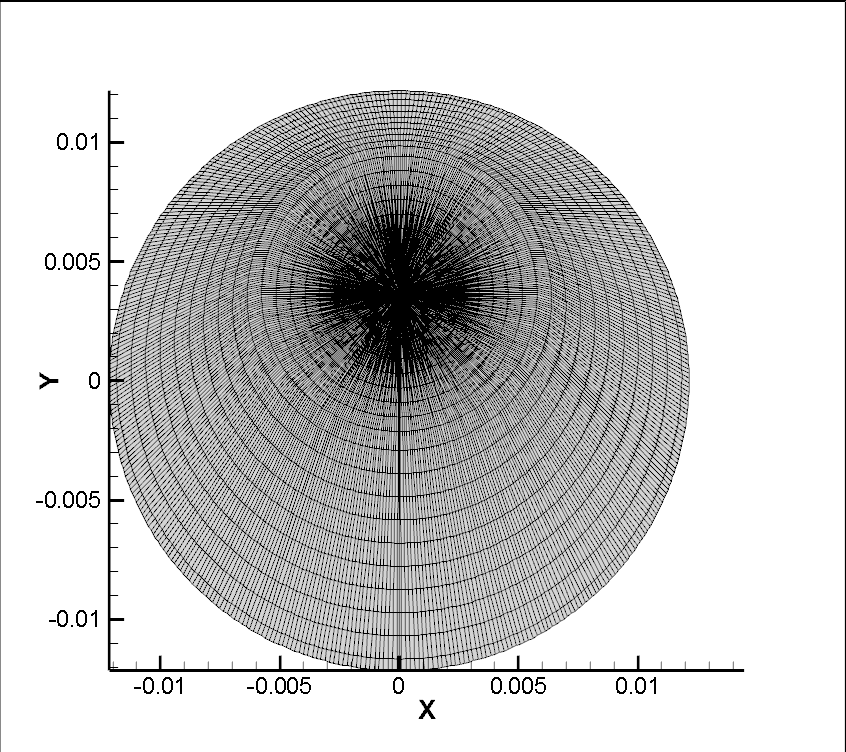
这个也是与标准结果不符合！！！
3.网格正交，采用非正交修正：

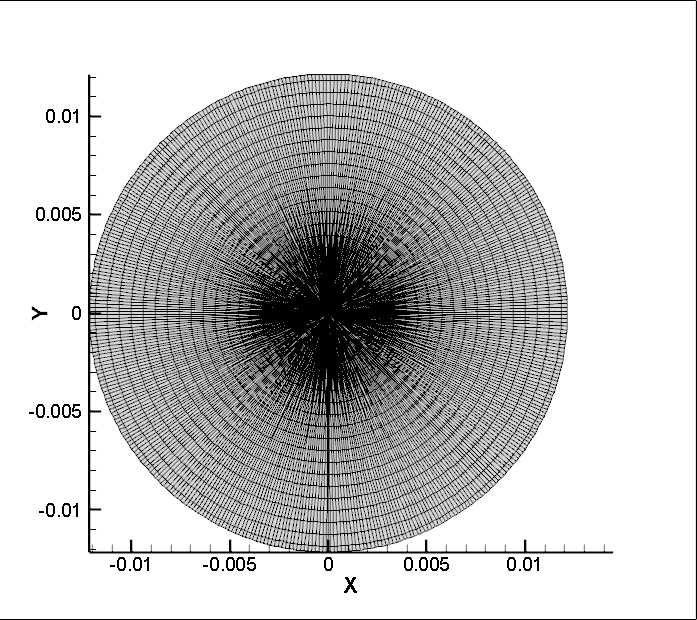
计算结果是正确的！
4.网格非正交，采用非正交修正：

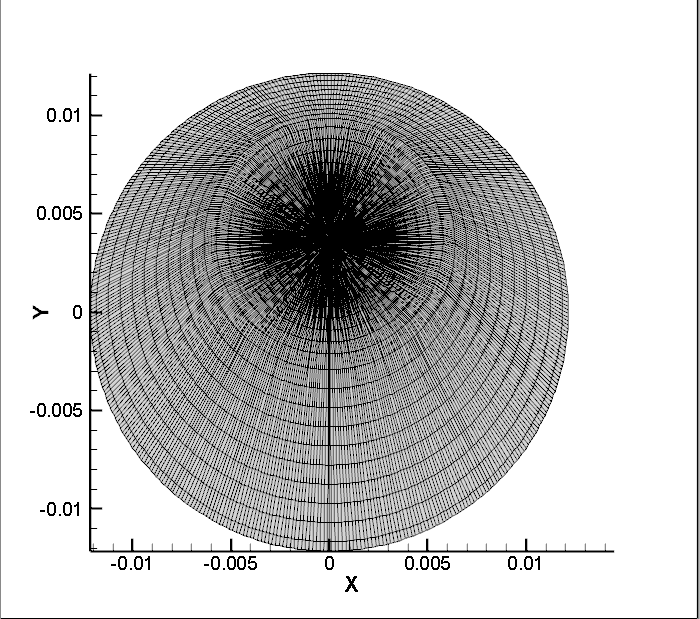
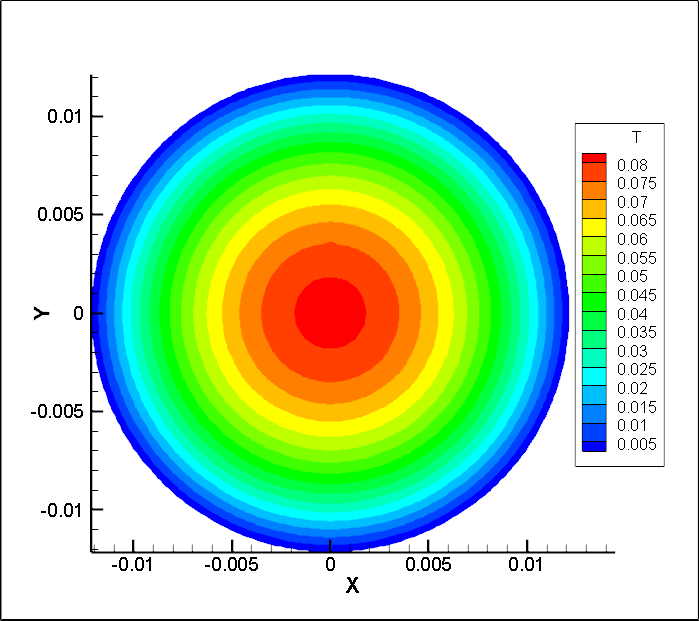
计算结果是正确的！
其实网格少点计算也是这样。非正交修正还是非常重要的！！！

李东岳

excellent

winsway_zero

@东岳
想咨询一下东岳老师，这两个梯度的区别，实在不知道怎么计算，谢谢谢谢~

李东岳

$\nabla\phi$就是求梯度后向面插值 $\overline{\nabla\phi}$是对当前网格与相邻网格所有网格点的梯度做平均

winsway_zero

@东岳

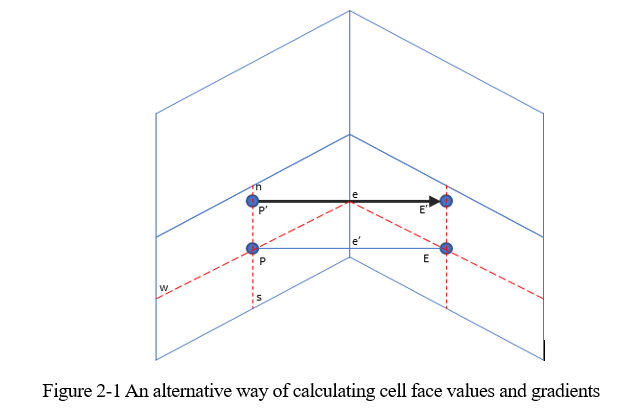
差分因子设定为：FX表示的是面上的插值因子，坐标和面相同。
\begin{equation}
FAC=\frac{\left| \overrightarrow{Pe} \right|}{\left| \overrightarrow{Pe} \right|+\left| \overrightarrow{eE} \right|}
\end{equation}
网格P和N格心之间的中间坐标e’计算：
\begin{equation}
{{P}_{{{e}'}}}={{P}_N}\times{FAC}+{{P}_P}\times{FACP}
\end{equation}
网格P和N格心之间的中间梯度计算：
\begin{equation}
\nabla {{\phi }_{e'}}=\nabla {{\phi }_{P}}^{old}FACP+\nabla {{\phi }_{N}}^{old}FAC
\end{equation}
网格P和N中间界面面心坐标e计算：
\begin{equation}
{{P}_{e}}=0.5({{P}_{1}}+{{P}_{2}})
\end{equation}
中间界面值$ϕ_e$的计算：
\begin{align}
& {{\phi }_{{{P}'}}}={{\phi }_{P}}+{{(\nabla \phi )}_{P}}\centerdot (\overrightarrow{{{r}_{P'}}}-\overrightarrow{{{r}_{P}}}) \
& {{\phi }_{e}}={{\phi }_{e'}}+{{(\nabla \phi )}_{e'}}\centerdot (\overrightarrow{{{r}_{e}}}-\overrightarrow{{{r}_{e'}}}) \
\end{align}

\begin{align}
& {{\phi }_{e}}={{\phi }_{E}}\times FAC+{{\phi }_{P}}\times FACP+{{\left( \frac{\partial \phi }{\partial x} \right)}_{e'}}\left( {{x}_{e}}-{{x}_{e'}} \right)+{{\left( \frac{\partial \phi }{\partial y} \right)}_{e'}}\left( {{y}_{e}}-{{y}_{e'}} \right) \
& ={{\phi }_{N}}FAC+{{\phi }_{P}}FACP+\nabla {{\phi }_{{{e}'}}}\bullet \left( \overrightarrow{{{r}_{e}}}-\overrightarrow{{{r}_{e'}}} \right) \
& ={{\phi }_{e'}}+{{(\nabla \phi )}_{e'}}\centerdot (\overrightarrow{{{r}_{e}}}-\overrightarrow{{{r}_{e'}}})
\end{align}

其中：$\overline{\nabla \phi }\text{=}\frac{1}{N}\sum\limits_{i}{\nabla {{\phi }_{i}},i=P,E,W,N,S}$,东岳老师这个是这样算吗？
参考文献：
[1]On the discretization of the diffusion term in finite-volume continuum mechanics
[2]Numerical method for coupled fluid flow, heat transfer and stress analysis using unstructured moving meshes with cells of arbitrary topology
[3]Ferziger J H, PeriC M.Computational Methods for Fluid Dynamics. 3. Germany: Springer,2002.
[4]Ferziger J H, PeriC M.Computational Methods for Fluid Dynamics. 4. Germany: Springer,2020.

winsway_zero

@东岳岳哥，帮忙看看呗，我写的公式是否正确，特别是梯度的算数平均那里哈~

李东岳

公事太多了我晕了

winsway_zero

@东岳
主要是这个哈

李东岳

文中说it represents the average of gradients at P and N_k，所以我理解是这样的

winsway_zero

@东岳谢谢东岳老师哈

CFD中文网

网格与圆管层流