LES定义入口速度的问题(DSRFG方法)
-
@xjwang 在 LES定义入口速度的问题(DSRFG方法) 中说:
@sunss
这个设置不是很难 你可以看一下这个视频 以及Eddylicious这个软件的document,他们里边也是用的这个边界条件
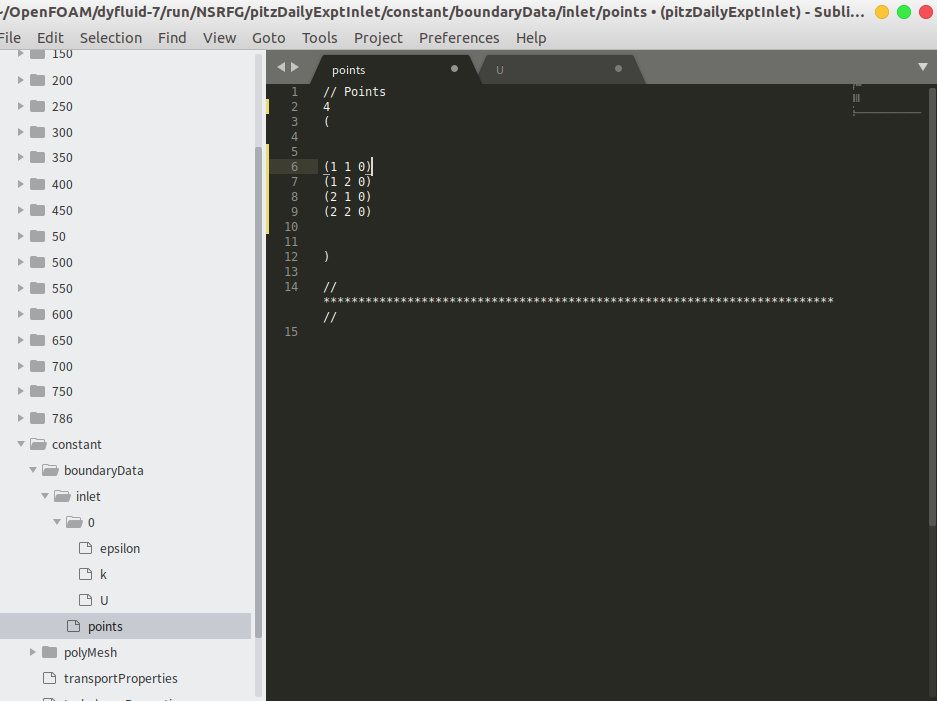
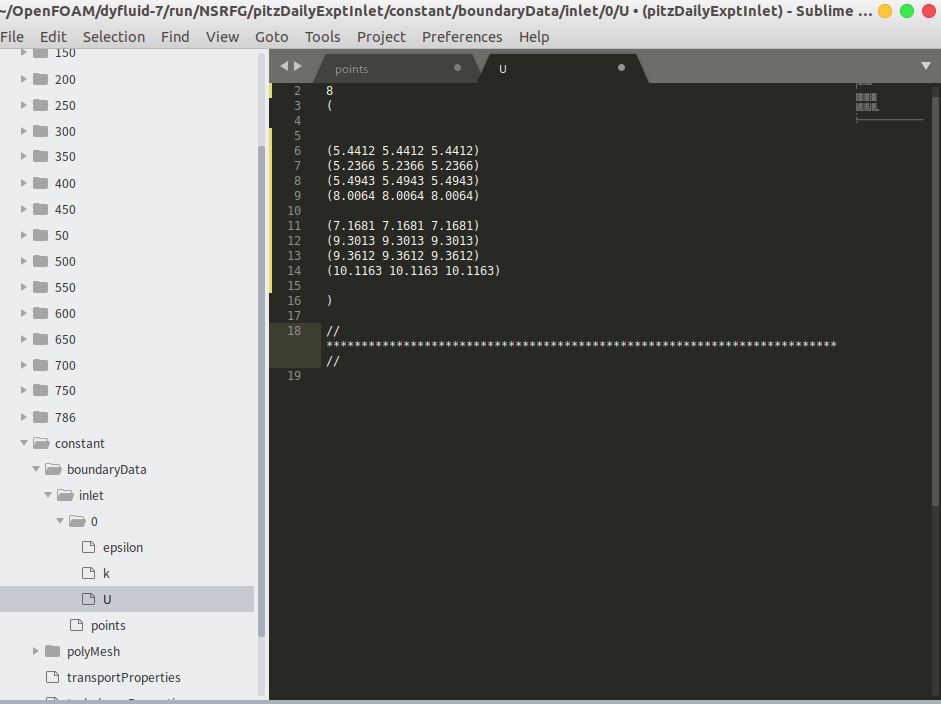
https://www.bilibili.com/video/BV1CV411C7Jr你说的这个视频和工具包,我之前都看了,没能找到解决方法。我简化一下问题,假设inlet面上只有四个点,分别是(1 1 0)(1 2 0)(2 1 0)(2 2 0),我要导入两个时间步的速度信息,也就是总共有八个速度的信息,那timeVaryingMappedFixedValue边界条件的point文件和U文件写成下面的形式行不行。
-
@霜染丹枫 在 LES定义入口速度的问题(DSRFG方法) 中说:
@李东岳 如李老师所言:“像是这种速度波动越往后越少的,类似开始有湍流后来无湍流”。我有个疑惑,采用中心差分格式的扩散项可以将扰动向四周传递,迎风格式的对流项具有迁移性,即可以将扰动向下游传递。从上面来看,入口的扰动应该是可以持续向下游传递的。如果几何轴向长度非常长的话,在很远的下游是不是也会保持一定湍流状态?还是由于壁面摩擦力及流体粘性对扰动有削减作用,在下游一直衰减甚至脉动全无,就是这种入口给定方法本身就会出现的现象呢?
湍流减少的现象应该是湍流生成方法不满足无散度条件,而像满足无散度条件ATSM-L这种方法下游湍流强度不仅不会减少,还会稍微增强。推荐你们去了解一下万嘉伟开发的一款湍流入口生成工具。https://nheri-simcenter.github.io/TinF-Documentation/examples/examples.html
-
@sunss
文件格式应该是:
points:
.......................................................
(
(1 1 0)
(0 1 0)
(1 0 0)
(0 0 0)
)
...........................................................
U:
..........................................................
(
(三维速度向量)
(三维速度向量)
(三维速度向量)
(三维速度向量)
)
.....................................................
所以你的设置有两个问题,一个是标出了4或者8这种数量,这个需要删掉,一个是需要把速度分别存储在对应的文件夹下边,不能在一个文件中。还有那些openfoam的星号可以删掉哈哈 -
@xjwang 在 LES定义入口速度的问题(DSRFG方法) 中说:
@sunss
文件格式应该是:
points:
.......................................................
(
(1 1 0)
(0 1 0)
(1 0 0)
(0 0 0)
)
...........................................................
U:
..........................................................
(
(三维速度向量)
(三维速度向量)
(三维速度向量)
(三维速度向量)
)
.....................................................
所以你的设置有两个问题,一个是标出了4或者8这种数量,这个需要删掉,一个是需要把速度分别存储在对应的文件夹下边,不能在一个文件中。还有那些openfoam的星号可以删掉哈哈多谢!已经成功导入风速数据。
-
@霜染丹枫
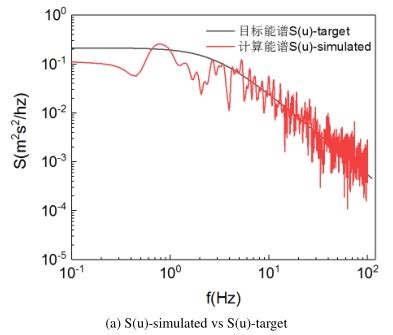
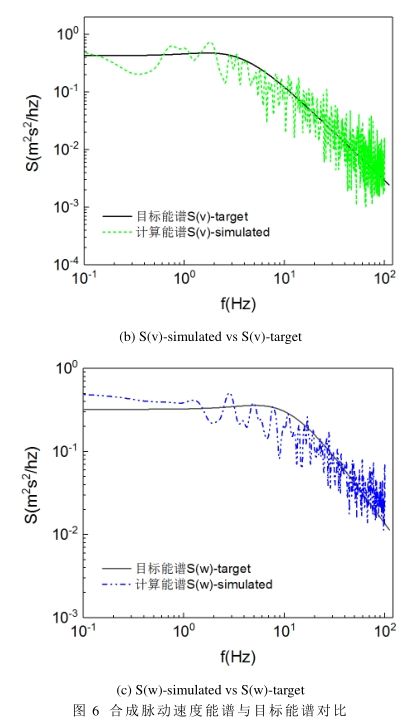
我做的风场模拟,所以我检察风洞模拟是否正确是通过检察计算域内的风速时程的功率谱是否和目标谱一致,也就是是否和在入口处生成的风速满足同样的能量分布。
不知道你们槽流最关心的是哪一个数值特征。比如,你可以验证turbulence intensity也可以验证power spectra,但不能通过一个瞬态的流场来判断模拟的好坏。一直不清楚你通过离散能量谱得到的脉动速度为什么要通过观察瞬时速度场来判断模拟的好坏,就算有很强的紊流特性也不能保证这个速度场的能量分布就和你目标谱一样。
上文中@sunss 同学说的那个tinf,你可以看一下,其中有dfsem, dfm等方法,特别是对于槽流,openfoam的tutorial中有一个RE395的算例(也许把名字记错了),应用的是DFSEM方法。
如@sunss 同学所说,也许高斯谱更适合你的功率谱,这样的话你可以直接应用fluent自带的那个对应RFG(Smirnov et al,2001)的生成方法,具体名字不记得了,你可以自己去查一下。
在其他回复中我提到过,DSRFG方法虽然理论上来说是无散度的,但如果应用在数值模拟中,就不是严格的无散度了,需要考虑网格尺寸,所以我一开始就问你网格尺寸和紊流积分尺度的数值。我们完成了一篇这样的论文,希望早点可以和你们分享。