CFD中的大涡模拟

李东岳

测试排版用

引言

湍流运动是目前计算流体力学中困难最多因此也最活跃的领域之一。当湍流存在，则住在其他相关的流动现象，并引致能量耗散、混合以及传热。没有三维的涡，则没有真正的湍流，因为只有在三维的流动中，涡旋才能进行伸展并产生新的涡旋。目前可采用的数值计算方法分为三类：直接模拟（Direct Numerical Simulation，DNS）、大涡模拟（Large Eddy Simulation，LES）和雷诺时均法（Reynolds-averaged Navier–Stokes，RANS）。RANS经过长期的发展，已经非常成熟。但RANS通过将速度进行平均后，并不能捕获湍流中的小涡结构。同时，这些小涡基本是各项同性的。另一方面，从主流中抽取能量的大涡却是各向异性，并且其和计算域的几何、边界、体积力高度关联。在使用RANS的时候，整个流场中必须使用同一个湍流模型对各种尺度下的湍流进行解析，但通常大涡和小涡的表现是不同的。因此研究学者对一种更完善的模型进行了探索。

不同于RANS，LES对大涡进行解析的同时对小涡进行模化。LES认为大涡直接受边界条件的影响因此对其解析，但小涡是各项同性的因此他们表现相同，可以进行模化。由于LES把小涡进行了模化，因此最小的网格单元需要大于Kolmogorov尺度（最小的涡旋尺度）。同时LES的时间步可以比DNS大的多。因此，对于给定的计算资源，相对于DNS，LES可以计算更大雷诺数的算例。另外，不同于RANS中平均的概念，LES使用的是一种空间滤波技术。LES模型的概念如下：

首先要确定一种滤波函数和截止尺度$\Delta$。这样，就可以对所有大于截止尺度的涡进行非稳态计算；
使用滤波函数对依时变量进行空间滤波操作，在这一步，小于截止尺度的涡被过滤掉；
在解析大涡和模化小涡的数学操作中，会产生一个亚格子尺度应力项（Sub-grid-scale Stress，SGS），亚格子尺度应力需要通过SGS模型来模化；

在LES中，截止尺度是用来表明“多大的涡才算大涡”的概念。其可以为任意大小，但是选择比网格还要小的截止尺度是没有意义的。在笛卡尔网格下，最简单的截止尺度这样计算：
\begin{equation}
\Delta=\sqrt[3]{\delta x \delta y \delta z}
\end{equation}
其中$\delta x$等为笛卡尔网格下网格单元的边长。其他不同的截止尺度计算方法还有最大边长法、普朗特混合长法等。

方程与模型

滤波N-S方程

笛卡尔坐标下的连续性方程为：
\begin{equation}
\frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \mathbf{U})=0
\end{equation}
对$\nabla \cdot(\rho \mathbf{U})$进行滤波后有滤波连续性方程：
\begin{equation}
\frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \mathbf{\bar{U}})=0
\end{equation}
其中$\mathbf{\bar{U}}$为滤波后的速度。且有：
\begin{equation}
\mathbf{U}=\mathbf{\bar{U}}+\mathbf{U'}
\end{equation}
其中$\mathbf{U'}$为残余速度，且$\mathbf{U'} \neq 0$。下图表示的是一个对$x$分量速度进行高斯滤波之后的滤波速度分量和残余速度分量的示意图。

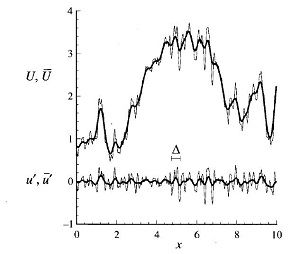
另外，有不可压缩动量方程为：
\begin{equation}
\frac{\partial \mathbf{U}}{\partial t}+\nabla \cdot (\mathbf{U} \mathbf{U})=-\nabla \frac{p}{\rho}+\nabla \cdot(\nu \nabla \mathbf{U})
\label{mom}
\end{equation}
同理有：
\begin{equation}
\frac{\partial \mathbf{\bar{U}}}{\partial t}+\nabla \cdot (\overline{\mathbf{U} \mathbf{U}})=-\nabla \frac{\bar{p}}{\rho}+\nabla \cdot(\nu \nabla \mathbf{\bar{U}})
\label{momF}
\end{equation}
在方程\eqref{momF}中，除了待求的$\bar{\mathbf{U}}$和$\bar{p}$外增加了一个未知量$\overline{\mathbf{U} \mathbf{U}}$。为了将问题简化，把方程\eqref{momF}的第二项进行变化：
\begin{equation}
\nabla \cdot (\overline{\mathbf{U} \mathbf{U}})=\nabla \cdot (\mathbf{\bar{U}} \mathbf{\bar{U}})+\left(\nabla \cdot (\overline{\mathbf{U} \mathbf{U}})-\nabla \cdot (\mathbf{\bar{U}} \mathbf{\bar{U}})
\right)
\label{W}
\end{equation}
将方程\eqref{W}带入到方程\eqref{momF}中有：
\begin{equation}
\frac{\partial \mathbf{\bar{U}}}{\partial t}+\nabla \cdot (\mathbf{\bar{U}} \mathbf{\bar{U}})=-\nabla \frac{\bar{p}}{\rho}+\nabla \cdot(\nu \nabla \mathbf{\bar{U}})
-\left(\nabla \cdot (\overline{\mathbf{U} \mathbf{U}})-\nabla \cdot (\mathbf{\bar{U}} \mathbf{\bar{U}})
\right)
\label{momFF}
\end{equation}
对比最初的的N-S方程\eqref{mom}，方程\eqref{momFF}中的最后一项$-\left(\nabla \cdot (\overline{\mathbf{U} \mathbf{U}})-\nabla \cdot (\mathbf{\bar{U}} \mathbf{\bar{U}})
\right)$为滤波操作产生的特殊项。对其展开有：
\begin{equation}
\nabla \cdot (\mathbf{\bar{U}} \mathbf{\bar{U}})=\nabla \cdot \left[\begin{matrix}
\bar{u}_1\
\bar{u}_2\
\bar{u}_3
\end{matrix}\right][\bar{u}_1, \bar{u}_2, \bar{u}_3]=\nabla \cdot \left[
\begin{matrix}
\bar{u}_1 \bar{u}_1 & \bar{u}_1 \bar{u}_2 & \bar{u}_1 \bar{u}_3\
\bar{u}_2 \bar{u}_1 & \bar{u}_2 \bar{u}_2 & \bar{u}_2 \bar{u}_3\
\bar{u}_3 \bar{u}_1 & \bar{u}_3 \bar{u}_2 & \bar{u}_3 \bar{u}_3
\end{matrix}
\right]
\label{T1}
\end{equation}

\begin{equation}
\nabla \cdot (\overline{\mathbf{U} \mathbf{U}})=\nabla \cdot \overline{\left[\begin{matrix}
u_1\
u_2\
u_3
\end{matrix}\right][u_1, u_2, u_3]}=\nabla \cdot \left[
\begin{matrix}
\overline{u_1 u_1} & \overline{u_1 u_2} & \overline{u_1 u_3}\
\overline{u_2 u_1} & \overline{u_2 u_2} & \overline{u_2 u_3}\
\overline{u_3 u_1} & \overline{u_3 u_2} & \overline{u_3 u_3}
\end{matrix}
\right]
\label{T2}
\end{equation}