fvc::intergrate(fvc::grad(phi))*nf不等于snGrad(phi)?
-
最近学习算法,绕来绕去把自己绕晕了,想问一下大家,下面这两个相等吗?
$(\nabla\phi)_f\cdot n_f$ 与 $snGrad_f(\phi)$
根据我的理解,对于同一个面,这两个表达式应该是相等的,都表示梯度在面法相方向的投影。但是我计算了一下,实际上怎么不想等?以如下一维网格为例:
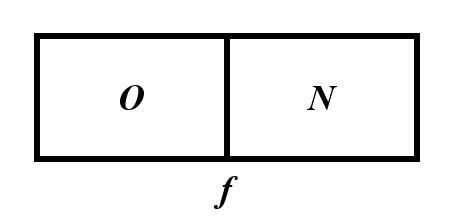
左右两侧的边界条件都是零梯度,如果设$\phi_O=1000$,$\phi_N=1, |d_{ON}|=1$,那么梯度可计算为:
$(\nabla\phi)_O = 1000\cdot(-1) + (1000+1)/2\cdot1 = -499.5$$(\nabla\phi)_N = (1000+1)/2\cdot(-1) + 1\cdot1 = -499.5$
f上的梯度为
$(\nabla\phi)_f = [(\nabla\phi)_O + (\nabla\phi)_N]/2 = -499.5$实际上就是:$(\nabla\phi)_f\cdot n_f = -499.5$
而snGrad根据定义可以直接计算
$snGrad_f(\phi) = \frac{\phi_N - \phi_O}{|d|} = -999.0$这两个值为什么不相等呢?是哪里出问题了?请各位大佬指点,非常感谢!
-
是的。你的计算是正确的。主要区别就是stencil。
snGrad是定义在面上的面法向梯度。就是你算的那个999。只涉及相邻的网格。interpolate(grad(phi)) & Sf的计算方法就是常规的计算网格上的$\nabla\phi$,然后再插值。如果你多写几个网格出来。会发现在某个面上,需要不相邻网格的梯度。你可以试一下给下面这样的场
|A|B|C|D|$$
sngrad=\frac{C-B}{\Delta x}
$$$$
grad=\frac{C-A}{4\Delta x}+\frac{D-B}{4\Delta x}
$$ -
@李东岳 非常感谢东岳老师。现在有点理解了,在Laplacian算子中用snGrad替代传统插值方法计算面上梯度来消除振荡,这是不是所谓的Rhie-Chow interpolation?
还有一个小问题,interfoam中动量方程的源项,如重力源项$\vec{g}\cdot\vec{x}\nabla\rho$等,我看是直接定义在面上了(代码中phig为$-(\vec{g}\cdot\vec{x})_f\cdot snGrad_f(\rho)\cdot |\vec{S_f}| \cdot rAU_f$),这个应该是传统的交错网格处理方式防止压强振荡?
-

