浸没边界法+超音速自定义求解器出现“浮点数例外，核心已转储”

[Rachel0096]

想请问一下大家，我采用的是rhoCentralFoam求解器，在里面耦合了浸入边界法（IBM）（直接力法），参考的是这篇文献《A pressure-corrected Immersed Boundary Method for the numerical simulation of compressible flows》（https://doi.org/10.1016/j.jcp.2018.07.033）。
在求解二维圆柱绕流自激振荡问题时，当运行了一段时间后，出现了“浮点数例外，核心已转储”，当求解固定的二维圆柱和二维圆柱受迫振荡时不会出现该问题。

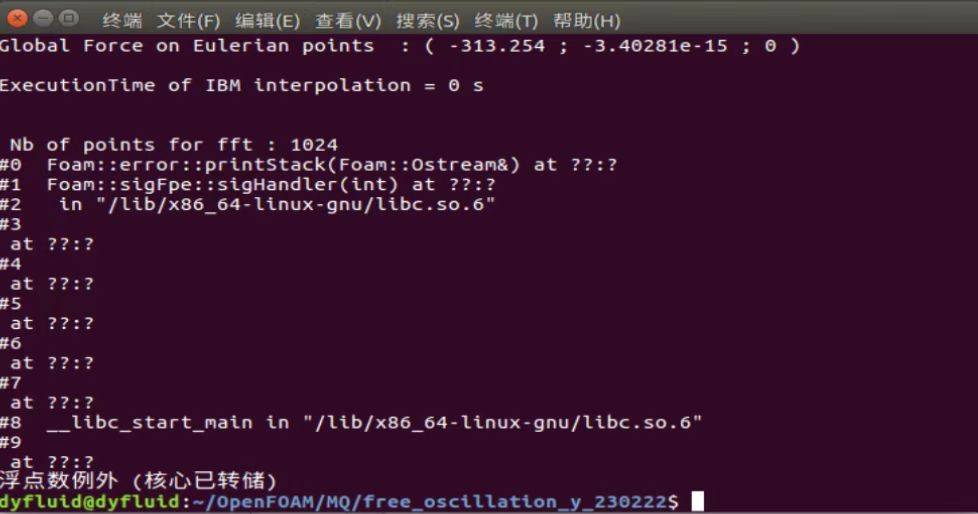
运动方程如下：



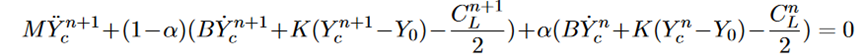
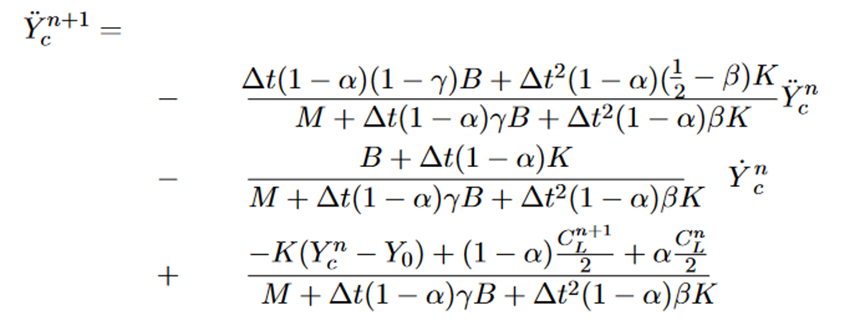
主要代码为：

if(structure_scheme == "HHT")
{
body.geometric_center_anp1.y() = - ( ( (1-body.hht_alpha)*dt*(1-body.newmark_gamma)*body.damping.y() + pow(dt,2)*(1-body.hht_alpha)*(0.5-body.newmark_beta)*body.spring.y() )		*body.geometric_center_an.y() + (  body.damping.y() + dt*(1-body.hht_alpha)*body.spring.y())*body.speed.y() + body.spring.y()*(body.geometric_center.y()-Equilibrium_mass_spring_damper_system.y())	+ (1-body.hht_alpha)*Force_corrected.y() + body.hht_alpha*body.old_global_force.y()  )/ (body.mass + dt*(1-body.hht_alpha)*body.damping.y()*body.newmark_gamma  + pow(dt,2)*(1-body.hht_alpha)*(body.newmark_beta)*body.spring.y()  ); 
displacement -=  body.geometric_center;
if(body.moving_direction.y() == 1) 
{
body.geometric_center.y() = body.geometric_center.y() + body.speed.y()*dt+ (pow(dt,2)/2)*( (1-2*body.newmark_beta)*body.geometric_center_an.y() + 2*body.newmark_beta*body.geometric_center_anp1.y()); 
body.speed.y() = body.speed.y() + dt* ( (1-body.newmark_gamma)*body.geometric_center_an.y() + body.newmark_gamma*body.geometric_center_anp1.y()); 					
}
else 
{
body.geometric_center.y() = body.geometric_center.y();
body.speed.y() = 0; 
}
displacement +=  body.geometric_center; 
body.geometric_center_an = body.geometric_center_anp1; 
}

想问一下出现浮点数溢出是什么原因呀？如果进一步缩短时间步长会有帮助嘛？

[李东岳]

rhoCentralFoam求解器缩小时间步长相对来说作用还是挺大的，因为本身是个显性求解器。不过因为你这个自己写的代码，debug起来并不容易。目前也不能给出更多的建设性意见。

[Rachel0096]

@李东岳 李老师，我把时间步长缩短为原来的1/10，现在能够计算下去啦，不会出现“浮点数例外，核心已转储”的问题

[李东岳]

我发现好多人都用直接力法植入IBM。这个方法属于IBM的主流方法？

[李东岳]

我看了一下这个直接力方法。挺有意思。直接力方法里面有一个desired velocity，这个速度对于固定的边界，是不是0？

https://doi.org/10.1016/j.jcp.2018.07.033 就是这篇文章里面，$\bfU^d=0?$

https://arxiv.org/pdf/1809.08170.pdf

[李东岳]

\begin{equation}
\frac{\bfU^{*}-\bfU^{n}}{\dt} = C^n + D^n + \mathbf{f}
\end{equation}

\begin{equation}
\mathbf{f}=\frac{\bfU^{d}-\bfU^{n}}{\dt} - C^n - D^n
\end{equation}

\begin{equation}
\bfU^{d}=0
\end{equation}

\begin{equation}
\mathbf{f}=-\frac{\bfU^{n}}{\dt} - C^n - D^n
\end{equation}

\begin{equation}
\bfU^{n} \rightarrow \bfU^{n}_L,C^n\rightarrow C^n_L,D^n\rightarrow D^n_L
\end{equation}

\begin{equation}
\mathbf{F}_L=-\frac{\bfU^{n}_L}{\dt} - C^n_L - D^n_L
\end{equation}

\begin{equation}
\mathbf{F}_L \rightarrow \mathbf{f}
\end{equation}

我的理解，直接应力IBM的算法就是这个样子，不知道对不对

[Rachel0096]

@李东岳 是的，李老师。
据我了解，目前常用的浸入边界法主要有直接力法、虚拟点法(the ghost-cell method)等，还有将玻尔兹曼方法与IBM方法相结合的玻尔兹曼-浸入边界法(IB-LBM)。
罗等人（2020 https://doi.org/10.1515/revce-2019-0076）根据D2区域将IBM方法分为the artificial boundary method和the authentic boundary method，对5种IBM做了总结。

[Rachel0096]

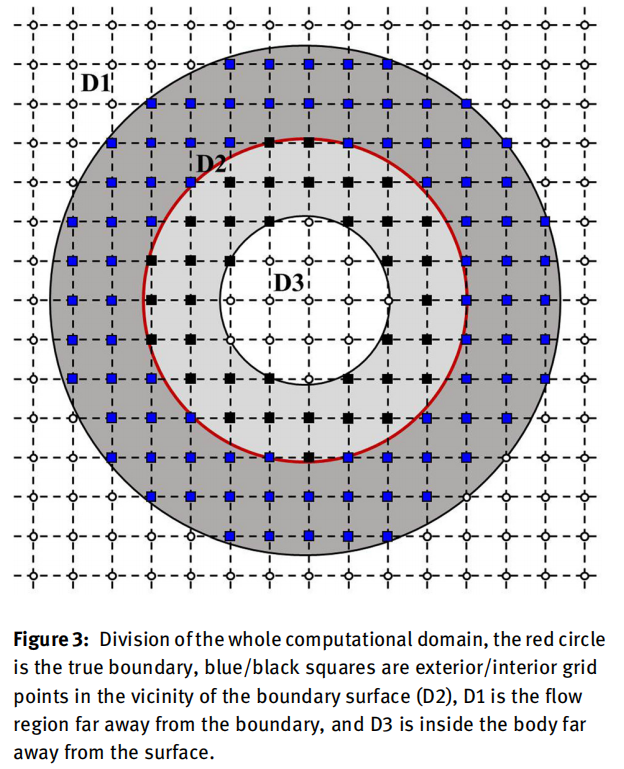
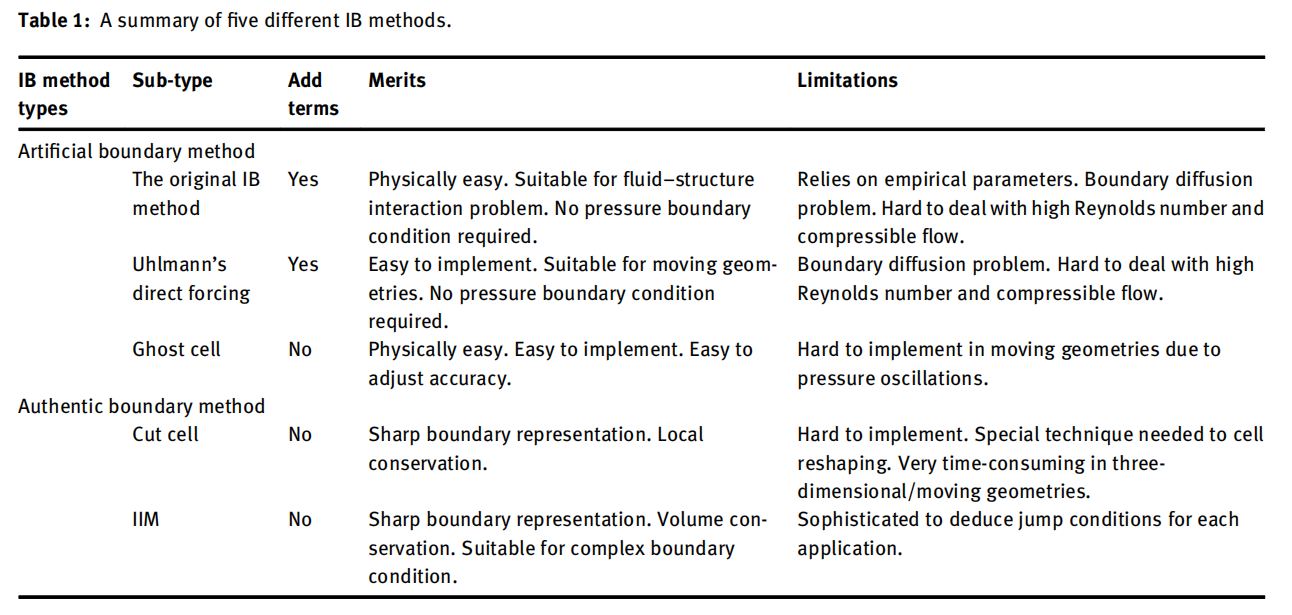
@李东岳 李老师，我对直接力法的理解是这样子的，可能不是很全面。
对于两相场（包含固体颗粒占据的区域）其控制方程为：
（其中f为内嵌边界对流体的作用力，与纯流场控制方程相比仅仅多了f项）

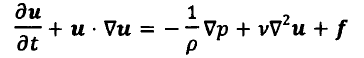
对于LFP(拉格朗日力点)处的流场应满足如下关系（将其他项用RHS(U)表示，定义在LFP上的流场变量用相应的大写字母表示，定义在EGP(固定欧拉网格点)上的流场变量用小写字母表示）：

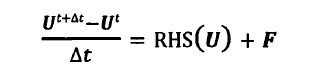
随后引入一个中间速度（假定其满足纯流场控制方程）

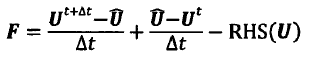
纯流场：

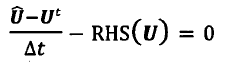
Ud就是您上述提到的desired velocity，对于固定的body，我们希望其满足Ud=0


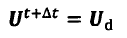
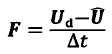
通过插值函数，可以实现F->f
得到f后便可更新流体场，得到相应的速度和压力：

[李东岳]

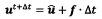
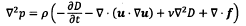
@Rachel0096 多谢多谢，我研究研究，要把细节扣一下

[李东岳]

看来关键步骤就是如何从欧拉场映射到拉格朗日场，以及从拉格朗日场映射到欧拉场。对于下面这个网格，存在网格体心以及网格面心，同时存在3个拉格朗日粒子。我在想他们的投影算法

[Rachel0096]

@李东岳 您可以看一下Uhlmann(2005)的这篇文章，An immersed boundary method with direct forcing for the simulation of particulate flows (https://www.sciencedirect.com/science/article/pii/S0021999105001385) ，目前很多直接力法都是在他的工作上进行改进的

[李东岳]

好的好的

我发现这个欧拉场到拉格朗日场，拉格朗日场到欧拉场的映射，有各种不同的方法..