Stokes流中的圆球绕流的阻力系数，怎么设置才能算准。

[李东岳]

使用symmetry边界，我还不知道如何检测边界面的速度

这个需要在求解器层面输出出来原始数据，用Info（麻烦一点）

[pengdi]

@李东岳 好的，东岳老师。明天我对比一下不同边界类型的圆柱绕流和方柱绕流计算，感觉曲面边界的影响可能会很大。

[Prometheus10]

@pengdi Pengdi老师，@李东岳 东岳老师
我来补充一下低雷诺数条件下（Re=0.1时）对圆球型壁面设置为symmetry或者slip边界的切向速度的结果：
依然是Wedge楔形网格的圆球绕流文件，然后将仿真结果在Paraview中用 plotOverLine提取：

首先是symmetry边界条件，第一个网格体心的速度大概是主流速度的1/2；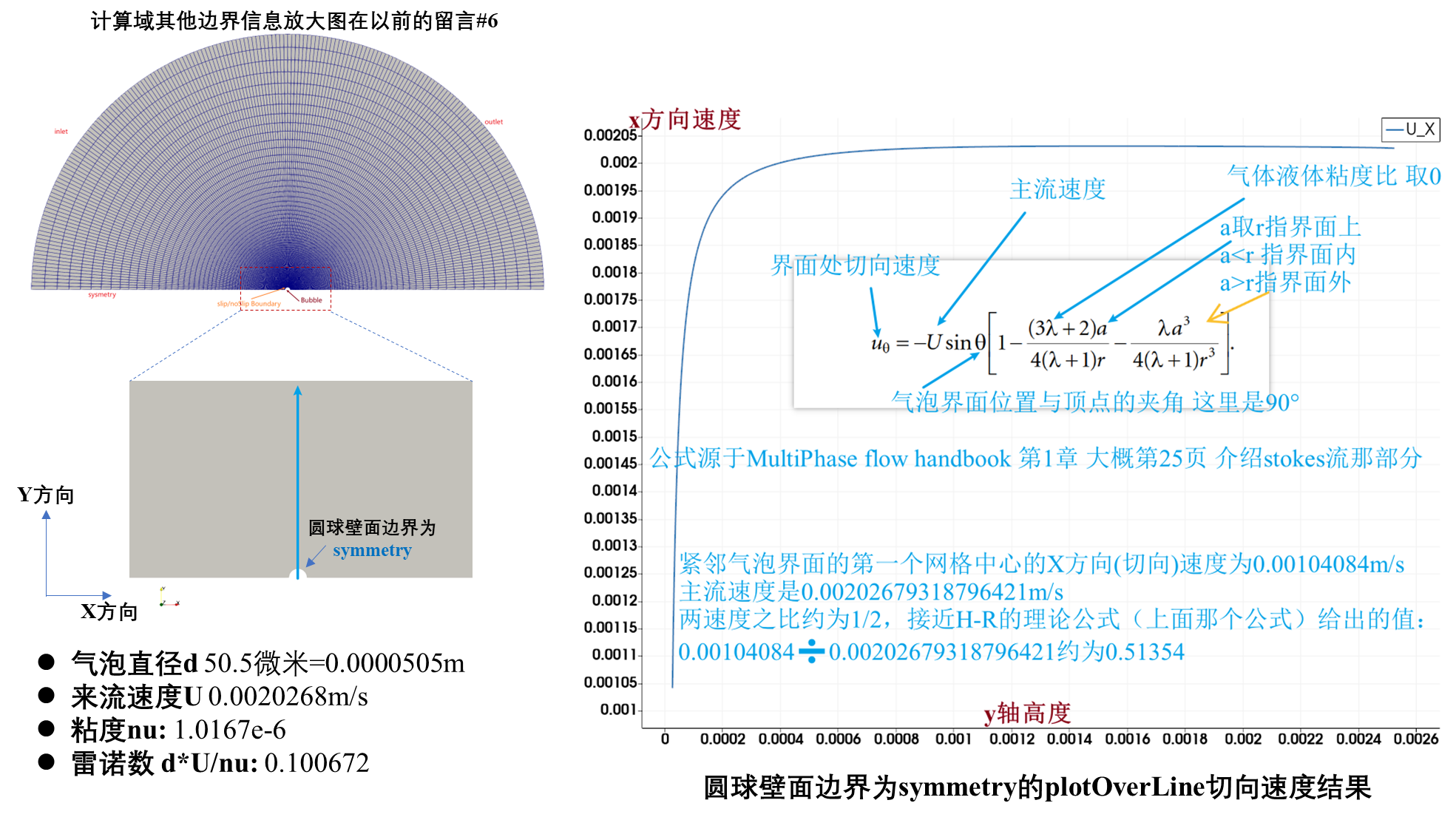

然后是slip边界条件，其第一个网格体心的速度就是主流速度；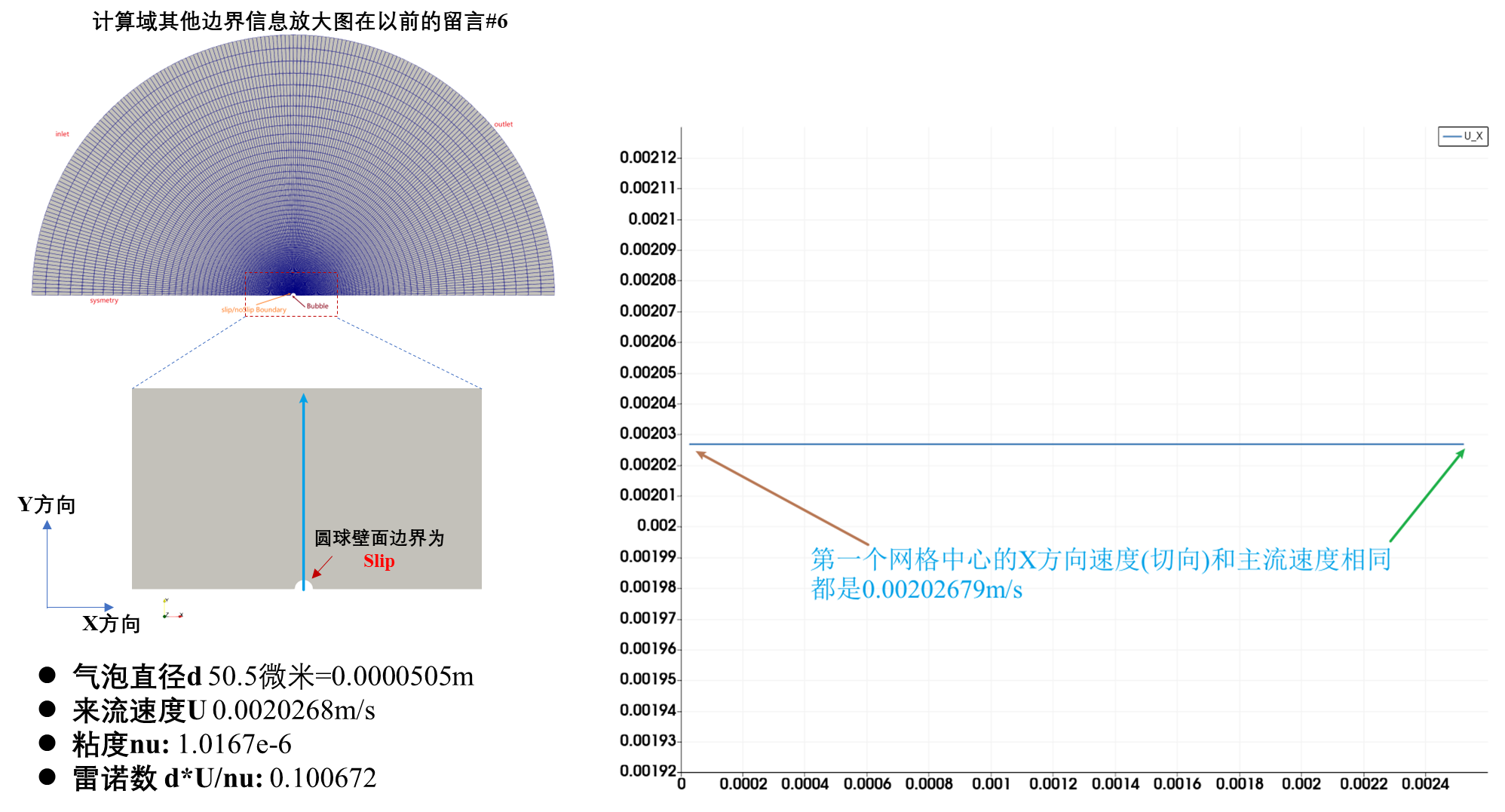

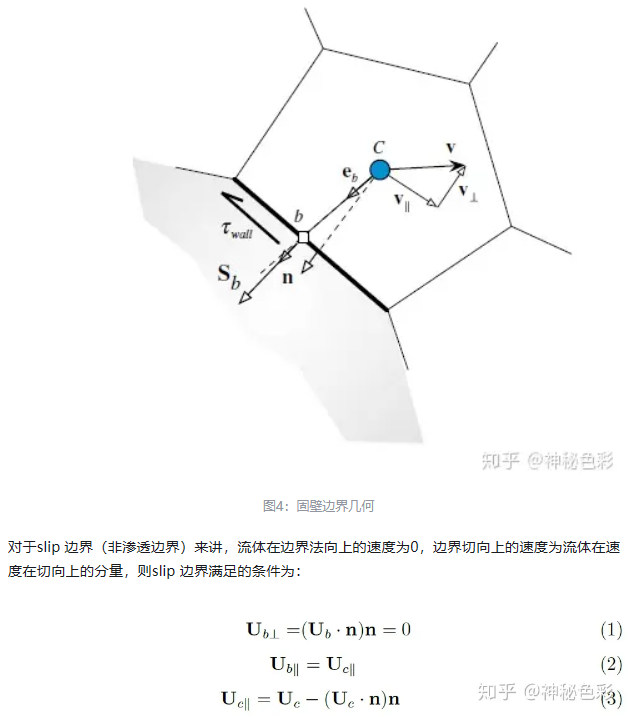
沿用一下这个示意图，symmetry边界也就是u·n=0确实很好描述了气泡界面处的速度分布，和Multiphase flow handbook第25页给出的公式也很吻合。(我这里给出的结果，准确来说，应该要说成是紧挨界面处，而不是界面上的切向速度，因为我只会用Paraview显示网格体心速度，还没能掌握如何用Info速度界面上的切向速度)
Michaelides, E., Crowe, C.T., Schwarzkopf, J.D., 2016. Multiphase flow handbook. CRC Press.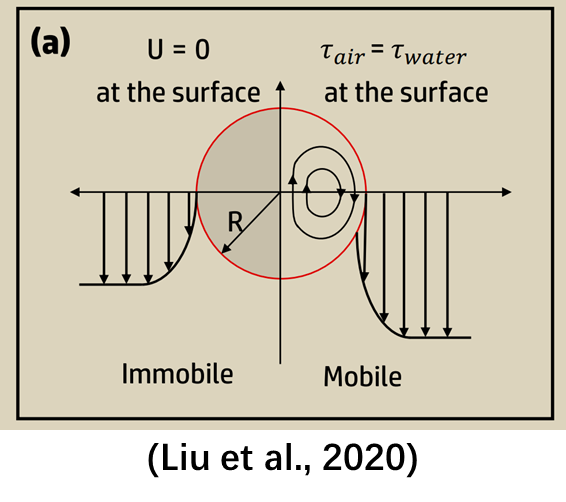

参考文献：
Liu, B., Manica, R., Xu, Z., Liu, Q., 2020. The boundary condition at the air–liquid interface and its effect on film drainage between colliding bubbles. Curr. Opin. Colloid Interface Sci. 50, 101374.

[pengdi]

@Prometheus10 您好，关于圆柱绕流的slip和symmetry边界计算我也计算对比过，我计算的雷诺数等于200，差别确实很大。我怀疑可能正方形绕流差别就没那么大了，今天比较忙，还没验证，我看明天能不能验证一下，稍后补充上来。

[Prometheus10]

@李东岳 东岳老师好，我现在想根据运行时计算得到的Cd值的大小反过来适配速度进口的速度大小，直至阻力和浮力平衡，通过看您其他帖子，好像需要在0/U文件夹下使用codedFixedValue边界来完成，想进一步咨询您：

在codedFixedValue如何调用当前时刻的Cd？

    inlet
    {
        type            codedFixedValue;
        value           $internalField;
        name            dragForceBalanceInlet; //name of new BC type
        code
        #{
            const fvPatch& inletPatch = this->patch();
            
            vectorField& vf = *this; 
            forAll(vf, i)
            { 
                scalar z = inletPatch.Cf()[i].y();
                scalar rhoL = 998.13;
                scalar rhoG = 1.225;
                scalar myG = 9.81;
                scalar myD = 0.0000505;
                vf[i].x() = sqrt(4*(rhoL-rhoG)*myG*myD/(3*Cd*rhoL));//想在这里调用Cd
                vf[i].y() = 0.0; 
                vf[i].z() = 0.0; 
            }
        #};
       
        codeOptions
        #{
              -I$(LIB_SRC)/finiteVolume/lnInclude \
              -I$(LIB_SRC)/meshTools/lnInclude
         #};
  
        codeInclude
         #{
                #include "fvCFD.H"
                #include <cmath>
               #include <iostream>
        #};
    }

上述代码是通过浮力和阻力的力平衡，得到阻力系数和速度的等式。

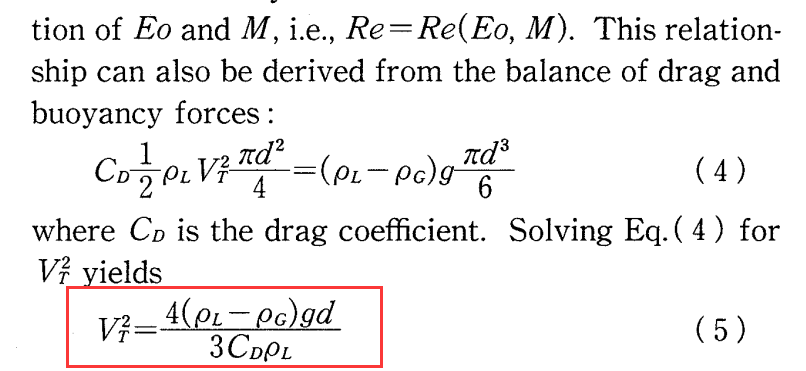
Tomiyama, A., Kataoka, I., Zun, I., Sakaguchi, T., 1998. Drag Coefficients of Single Bubbles under Normal and Micro Gravity Conditions. JSME International Journal Series B 41, 472–479.

[李东岳]

Cd这个在forceCoeff.C里面计算出来的，这个我看没有公开的接口，也不知道哪个是先声明的。另外一个方法是是你自己计算一下Cd。

$$
Cd=\frac{\left( \sum p_f\bfS_f + \sum \bfS_f\cdot \tau_f \right)\cdot\mathbf{direction}_{drag}}{(\sum|\bfS_f|) \frac{1}{2}\rho|\bfU|^2}
$$

里面的$\tau$定义在eddyViscosity里面的sigma()，被称之为R。不过我不确定能否在codedFixedValue里面去引用（不确定这个前后关系是哪个先声明的）

[Prometheus10]

@李东岳 好的，谢谢东岳老师。

[Prometheus10]

@pengdi @李东岳
东岳老师， PengDi老师，您们好

我目前仍然有一点没有想明白，想再请两位老师指点：

首先是Slip边界条件的定义：
【在界面处，法向速度为0，同时切向速度的梯度为0.】

沿用知乎博主的解析神秘色彩OpenFOAM 边界条件系列解析—Slip边界

COMSOL的帮助文档也是一致的内容
Theory for the Wall Boundary Condition

再有是东岳老师在#44楼所提到的：

因为slip是衍生来自symmetry，因此切向方向二者处理是一样的，都是零梯度。

那么，slip和symmetry按道理都应该同时符合这几个公式
$\mathbf{U}_{b\perp}=(\mathbf{U}_b\cdot\mathbf{n})\mathbf{n}=0$
$\mathbf{U}_b{|}=\mathbf{U}_c{|}$
$\mathbf{U}_c{|}=\mathbf{U}_c-\left(\mathbf{U}_c\cdot\mathbf{n}\right)\mathbf{n}$

但是，当Slip和Symmetry应用到弯曲边界的时候：为什么速度有这么大的差异，并由此得出的阻力系数也大不相同。
雷诺数Re=1时，阻力系数：
CD(slip)=13.49,
CD(symmetry)=17.6

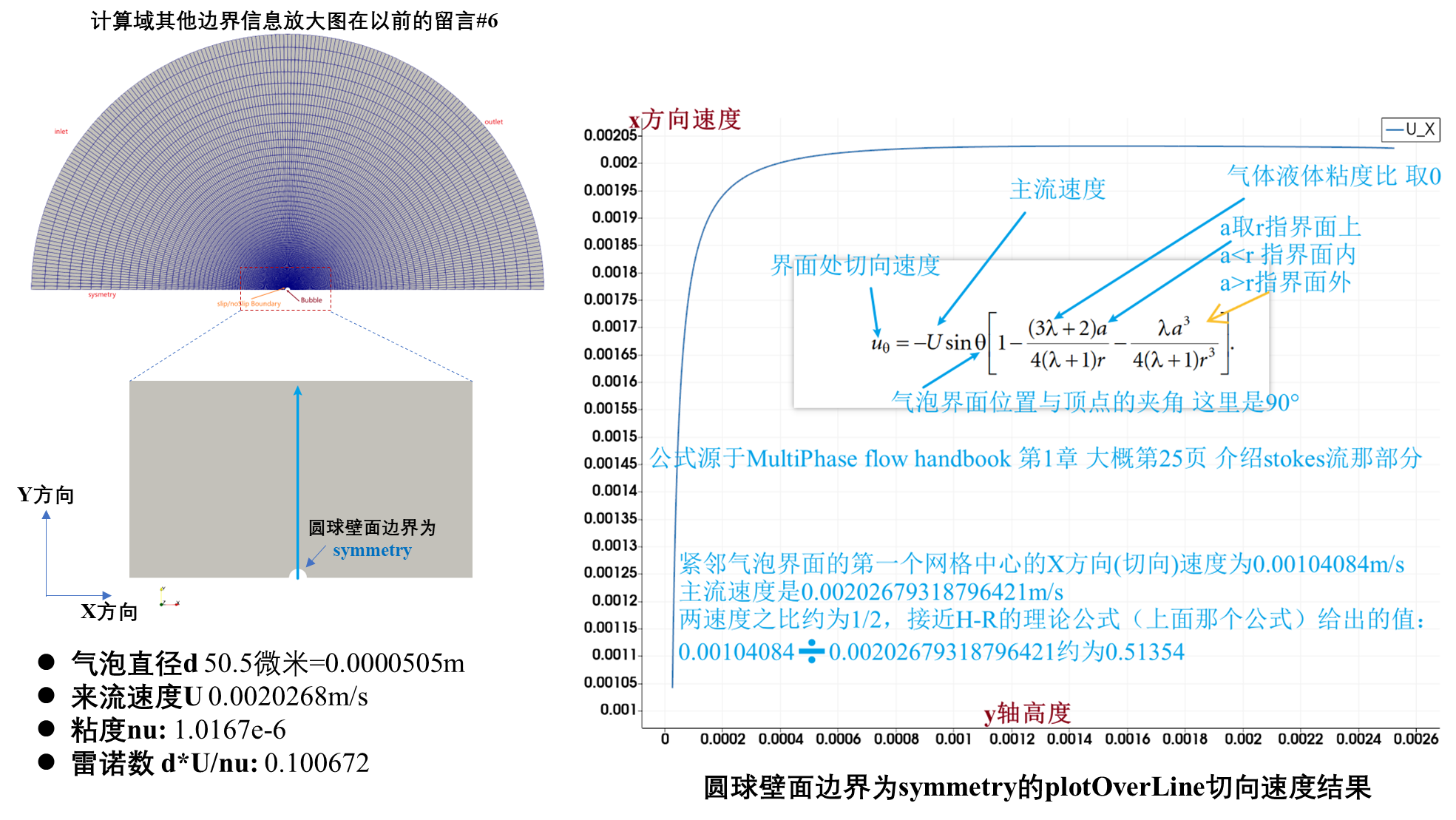
从以上两个图结果上来看：
Symmetry的速度明显是和主流速度之间渐变过渡的（左图蓝线，大概从U/2逐渐发展到U），也就意味着流体在界面处是受到切应力的；
而Slip的速度是和主流速度一致（左图蓝线，Slip界面处就是和主流速度一样的U），因此我认为：

symmetry条件应用到弯曲边界的时候，并不会对弯曲边界的切应力做限制，因此弯曲边界的symmetry条件只是以下表达式：
$\mathbf{U}_{b\perp}=(\mathbf{U}_b\cdot\mathbf{n})\mathbf{n}=0$

此时Symmetry已经不再等同于Slip条件，其真实意义已经为：

Symmetry：【在界面处，法向速度为0，同时切向速度的梯度可以不为0.】
而Slip依然是：【在界面处，法向速度为0，同时切向速度的梯度为0.】

不知道这样理解是否正确？

[李东岳]

从你的结论来看，symmetry确实存在切应力，这与我之前的理解是相反的。但是基金会那本书里面也写了，symmetry是所有的场都是symmetry，是一种更严厉的限制。但是目前来看像是相反的。目前我在备课还不能细看。你这个问题（symmetry与slip边界），还有论坛里面有个时间步长越小结果越差的，成了老大难了。。感觉是非常底层的bug。

[pengdi]

@Prometheus10 对 如果这样理解的话 为什么symmetry计算结果和理论解更相近呢