不可压缩流动中的能量方程
-
各位老师好,
我在处理不可压缩能量守恒时,希望通过分析能量守恒中的各项变化来分析能量流动方向,但是碰到几个问题,请大家指导。
参考《计算流体力学基础及其应用》推导能量方程:
流体微团的能量变化率=流入的净热流+体积力功率+表面力功率
体积力
可以表示为

表面力
分为正压力和切应力,只考虑一个方向的分量
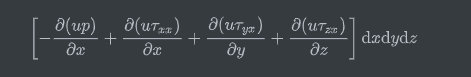
综合三个方向,简化表示为

其中第一项表示可逆的做功过程,第二项为粘性耗散。进一步的这两项各可以拆为两项

净热流
分为热源(辐射等)和传导
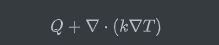
能量变化率
这里取守恒形式,将物质导数展开
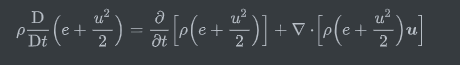
所以总的能量方程可写为
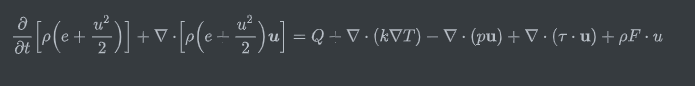
现在考虑不可压缩流动中,没有外力和热源及温度变化,方程退化为如下形式
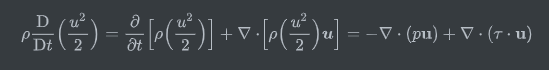
将其化简并展开
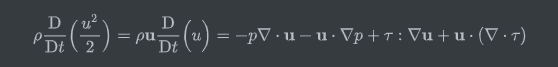
这里我们比较动量方程和连续性方程
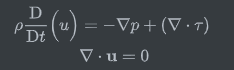
可以消掉能量方程的部分,得到如下表达
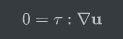
也就是说不可压缩流动中,如果不考虑温度变化,粘性耗散项没有作用是能量守恒的基础。那么当我们考虑这样一个具体问题,不可压缩的圆柱涡激振动,能量守恒的物理意义应该如何表达,是否可以写成如下形式

在全场积分即
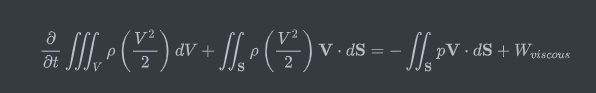
我的问题是:
1.这个积分式子的物理意义是
计算域内的能量变化率=所有边界压力功率+所有边界剪切应力功率还是说
计算域内的能量变化率=所有控制体积上的压力功率+所有控制体积上的剪切应力功率
2.这样就不存在分析各项变化来找到能量流动方向了,主要希望分析流场和结构间的能量流动方向。
-
谢谢老师回复,我通过代码输出每个时间步对应的量,发现并没有守恒性。如果理论推导没有问题,可能代码的对应出错了,麻烦帮我看一下:
// 计算速度场的梯度 scalar rho = 1000; // 流体密度 const scalar mu = 1e-3; // 粘性系数 tmp<volTensorField> gradUTmp = fvc::grad(U); const volTensorField& gradU = gradUTmp(); // 初始化总的B3和剪切通量 scalar totalB3 = 0.0; scalar totalViscousFlux = 0.0; // 遍历所有边界patch forAll(mesh.boundaryMesh(), patchI) { const polyPatch& patch = mesh.boundaryMesh()[patchI]; word patchName = patch.name(); // 如果对特定的patch感兴趣,可以添加条件检查 if ((patchName == "front")||(patchName == "back")) { continue; // 跳过名为"front"或"back"的边界 } // 初始化当前patch的B3和剪切通量 scalar B3Patch = 0.0; scalar ViscousFluxPatch = 0.0; // 循环遍历patch上的所有面 forAll(patch, faceId) { const vector& Sf = patch.faceNormals()[faceId]; // 从patch对象获取归一化法向向量 scalar faceArea = mag(patch.faceAreas()[faceId]); // 计算面积向量的模长作为实际面积 const vector& U_boundary = U.boundaryField()[patchI][faceId]; const Tensor<double>& faceGradU = gradU.boundaryField()[patchI][faceId]; // 计算应力张量(包含法向和切向应力) Tensor<double> stressTensor = mu * (faceGradU + faceGradU.T()); // 计算壁面剪切应力(只保留切向分量) vector wallShearStress = stressTensor & Sf; wallShearStress -= (wallShearStress & Sf) * Sf / (magSqr(Sf) + VSMALL); // 壁面剪切应力与速度的点积 scalar wallShearStressDotU = wallShearStress & U_boundary; const volScalarField& pressure = mesh.lookupObject<volScalarField>("p"); scalar p_boundary = pressure.boundaryField()[patchI][faceId]; scalar pressureFlux = p_boundary * (U_boundary & Sf); // 根据面积加权的壁面剪切应力与速度的点积以及压力与速度的通量 ViscousFluxPatch += faceArea * wallShearStressDotU; B3Patch += faceArea * pressureFlux; } // 输出当前边界上的B3和剪切通量 Info << "Patch: " << patchName << ", Integrated B3: " << B3Patch << ", Integrated Viscous Flux: " << ViscousFluxPatch << endl; // 将当前patch的B3和剪切通量累加到总和中 totalB3 += B3Patch; totalViscousFlux += ViscousFluxPatch; } // 输出总的B3和剪切通量 Info << "Total Integrated B3 on all patches: " << totalB3 << endl; Info << "Total Integrated Viscous Flux on all patches: " << totalViscousFlux << endl; // 计算域内的能量变化率(仅考虑动能) volScalarField kineticEnergy = 0.5 * rho * magSqr(U); scalar totalKineticEnergyOld = 0.0; scalar totalKineticEnergyNew = 0.0; forAll(kineticEnergy, cellI) { totalKineticEnergyOld += kineticEnergy.oldTime()[cellI] * mesh.V()[cellI]; totalKineticEnergyNew += kineticEnergy[cellI] * mesh.V()[cellI]; } scalar energyChangeRate = (totalKineticEnergyNew - totalKineticEnergyOld) / runTime.deltaTValue(); Info << "Total Kinetic Energy (old): " << totalKineticEnergyOld << " J" << endl; Info << "Total Kinetic Energy (new): " << totalKineticEnergyNew << " J" << endl; Info << "Kinetic Energy Change Rate in the domain: " << energyChangeRate << " W" << endl; runTime.printExecutionTime(Info); }
