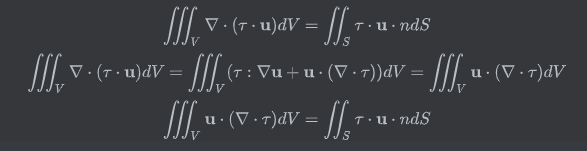入口粘性功率的准确计算

ice_flow

各位老师好，

我在计算管道流粘性功率时使用两种积分方案得到的结果误差很大。
在数学上，体积分可以转换为面积分。

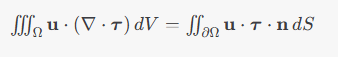
我先用整个计算域内的网格计算左边的体积分，得到的值很接近预测值。
再使用右侧的面积分计算几个边界，却得到很小的值。管道流动如下：
左侧入口：充分发展的速度入口，计算得到的面积分很小（接近0）
右侧出口：给定压力出口（0），他的速度梯度是0，所以在这个边界上的面积分是0，和计算得到的值匹配
两侧壁面：无滑移壁面壁面速度为0，所以边界上的面积分也是0，和计算也相符

问题是出口和壁面都是由于给定的边界条件导致的数值为0，那么入口的面积分结果应该很接近左侧的体积分值才对。

我自己分析是由于入口的速度梯度很难准确计算导致的。所以我使用入口右侧一层的网格速度梯度来代替，但是结果仍然很小。请教大家。

李东岳

你这个高斯定律用的不对，我还没见过这么用的，你确定这么用是对的么

ice_flow

@李东岳抱歉老师，之前的写法有问题，重新补充一下。

这里也是有相同的问题，如果入口使用了充分发展的速度条件，管道流稳定后沿流方向不存在速度梯度，按照面积分的方法求得的结果应该也是0.

李东岳

为什么略去$\tau : \nabla\bfU$，如果略去的话，$\nabla\cdot(\tau\cdot\bfU)$也应该略掉
$\int\nabla\cdot(\tau\cdot\bfU)\rd V$以及$\int(\tau\cdot\bfU)_f\cdot\rd\bfS_f$，这些都是连续形式，离散形式你是怎么计算的

ice_flow

@李东岳
老师好，我分开回答
1.这里略去的原因是
在总的能量方程中：

如果不考虑热源、辐射、外力和温度变化。方程可以写成

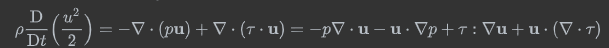
再考虑动量方程，就得到

因为不可压缩，所以这项就为零，省略去了。
2.离散的形式我没有自己展开，使用的下面代码，这是体积分

// 计算应变速率张量的偏量（deviatoric part of the strain rate tensor）
volTensorField devD = dev(gradU);

// 计算粘性应力张量
volTensorField tau = mu * devD;

// 计算粘性功率密度
volScalarField viscousPowerDensity = U & fvc::div(tau);

// 计算整个计算域的粘性功率（体积分）
scalar totalViscousPowerVolume = 0.0;
forAll(viscousPowerDensity, cellI)
{
    scalar cellVolume = mesh.V()[cellI];
    totalViscousPowerVolume += viscousPowerDensity[cellI] * cellVolume;
}

Info << "Total viscous power in the domain (volume integral): " << totalViscousPowerVolume << endl;

这部分是面积分，有点长

// 计算粘性功率（面积分）
scalar totalViscousPowerSurface = 0.0;

// 定义入口ID
label inletPatchID = mesh.boundaryMesh().findPatchID("inlet"); // 假设入口补丁名为 "inlet"

forAll(mesh.boundaryMesh(), patchI)
{
    const polyPatch& patch = mesh.boundaryMesh()[patchI];
    const word patchName = patch.name();

    const fvPatchVectorField& U_patch = U.boundaryField()[patchI];
    const fvPatchTensorField& tau_patch = tau.boundaryField()[patchI];

    scalar patchViscousPower = 0.0;

    forAll(patch, faceI)
    {
        const vector& Sf = patch.faceAreas()[faceI];
        const vector& U_face = U_patch[faceI];
        tensor tau_face;

        if (patchI == inletPatchID)
        {
            // 计算入口速度梯度的估计
            label cellI = patch.faceCells()[faceI];

            // 使用有限差分法计算速度梯度
            scalar dx = mesh.V()[cellI] / mag(Sf); // 单元在面法向量方向上的长度
            tensor gradU_approx = tensor::zero;
            gradU_approx.xx() = 2 * U_face.x() / dx; // x 方向上的速度梯度
            gradU_approx.yy() = 2 * U_face.y() / dx; // y 方向上的速度梯度
            gradU_approx.zz() = 2 * U_face.z() / dx; // z 方向上的速度梯度
            //Info << "dx: " << dx << endl;
            tau_face = (2.0/3.0) * mu * gradU_approx;
        }
        else
        {
            tau_face = tau_patch[faceI]; // 正常计算
        }

        scalar viscousPowerFace = (tau_face & U_face) & Sf;
        patchViscousPower += viscousPowerFace;

        // 输出壁面上的速度梯度和粘性应力张量的值
        if (patchName == "inlet")
        {
            Info << "patch: " << patchName << ", face: " << faceI << endl;
            Info << "U_face: " << U_face << endl;
            Info << "tau_face: " << tau_face << endl;
            Info << "Sf (face normal vector): " << Sf << endl;
			
            Info << "viscousPowerFace: " << viscousPowerFace << endl;
        }
    }

    totalViscousPowerSurface += patchViscousPower;
    Info << "Patch: " << patchName << ", Integrated viscous power: " << patchViscousPower << endl;
}

李东岳

$\nabla\cdot(\tau\cdot\bfU)$这一项，一般只有在超音速的时候才会考虑贡献

代码我粗略看了一下，为什么inlet要单独计算？另外你写成数学形式更好debug。不过数学形式很简单，所以大概率还是代码里面可能有问题需要debug

ice_flow

@李东岳
谢谢老师，一开始我认为是入口的速度梯度计算的不准确，所以用差分方法直接计算。后面对照下看来是接近的。
我认为可能是不可压缩的算法里不考虑严格的能量守恒，所以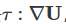直接计算并不为0.
但是上面公式推导中使用高斯方法转换体面积分的时候默认了不可压缩时这项为零。应该写出完整的形式计算

Total viscous power in the domain (volume integral): -1.50451907
Total integrated tau : gradU: 1.48509576
Total integrated viscous power (surface): 0.00384099619

这样计算后数值是接近的，等稳定后误差应该还会减小。

CFD中文网

入口粘性功率的准确计算