通量分裂在多相流中的应用小测验
-
虽然通量分裂在求解双曲方程中非常重要并且衍生出各种格式,但是在多相流中通量分裂也是一种保持变量的可实现性(Realizability)的好方法。同时,通量分裂方法还可以降低耗散。
在多相流的通量方法中,网格单元的面的通量被分裂为左边和右边两个通量,这个面上的通量分别依据各自的迎风格式来计算。在常规方法中,给定一个通量,在OpenFOAM中的代码可以写为:
fvm::ddt(U) + fvm::div(phi, U)在通量分裂主动计算通量之后,类似的代码主要为这种形式:
fvm::ddt(U) + fvc::div(phi)区别主要在于后者的通量已经通过分裂的方法计算。
下面一张图是采用常规离散方法和通量分裂的方法对比的结果,那种耗散性更低一目了然,在网格进一步细化的时候,耗散会变得更低逼近精确解。
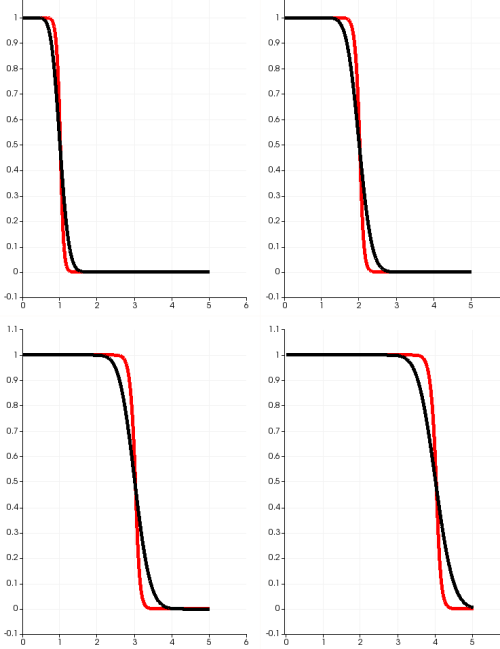
更多关于通量分裂可参考:
LeVeque, Randall J. Finite volume methods for hyperbolic problems. Vol. 31. Cambridge university press, 2002.
MULES也是一种降低耗散同时保证有界的方法,但是其思路主要跟随TVD格式而不是通量分裂。
