网格只是全都正交的空计算域网格,还是有放几何的网格。记得之前用ICEM的 o-block 画的方柱网格,看起来质量还行,其实网格质量很差,用fluent的PISO求解器都发散
coolhhh
帖子
-
网格y+求助 -
张量二阶偏导数 偏(A_j B_i)/偏(x_i x_j) 如何编程@学流体的小明
问了AI,OpenFOAM需要手动做两次梯度计算#include "fvCFD.H" // OpenFOAM 的核心头文件,包含 mesh、field、fvc/fvm 工具 #include "fvcGrad.H" // 显式声明 fvc::grad int main(int argc, char *argv[]) { #include "setRootCase.H" #include "createTime.H" #include "createMesh.H" // 创建速度场 U volVectorField U ( IOobject ( "U", runTime.timeName(), mesh, IOobject::MUST_READ, IOobject::AUTO_WRITE ), mesh ); // 把 u1 分离出来 volScalarField u1 = U.component(vector::X); // 或者 U.x() // 1. 计算 u1 的一阶梯度 ∇u1 volVectorField gradU1 = fvc::grad(u1); // gradU1.x() = ∂u1/∂x1 // gradU1.y() = ∂u1/∂x2 // gradU1.z() = ∂u1/∂x3 // 2. 对 ∂u1/∂x1 这个标量场,在 x2(Y)方向再求一次梯度 // fvc::grad(gradU1.x()) 是一个 volVectorField, // 其中 .y() 即 ∂(∂u1/∂x1)/∂x2 = ∂²u1/∂x1∂x2 volScalarField d2u1dx1dx2 = fvc::grad( gradU1.x() ).y(); // 写入结果 d2u1dx1dx2.write(); return 0; } -
snappyHexMesh的加密以及在直角处的边界层生成问题@studentTan nCellsBetweenLevels 过渡层设置多一点,试下10层或20层
nCellsBetweenLevels 1; -
snappyhexMesh划分边界层网格时在锐角处无法生层边界层- 试下 snapControls 用 explicitFeatureSnap
snapControls { implicitFeatureSnap false; explicitFeatureSnap true; }- 同时把 meshQualityDict 质量要求降低,因为这种尖角边界层网格质量就是挺差
maxBoundarySkewness 10; maxInternalSkewness 4; minDeterminant 0.001; minFaceWeight 0.02; minVolRatio 0.01;- 按上面方式可能能生成这样的边界层网格,网格质量差,有可能会导致计算发散,得具体试算下
-
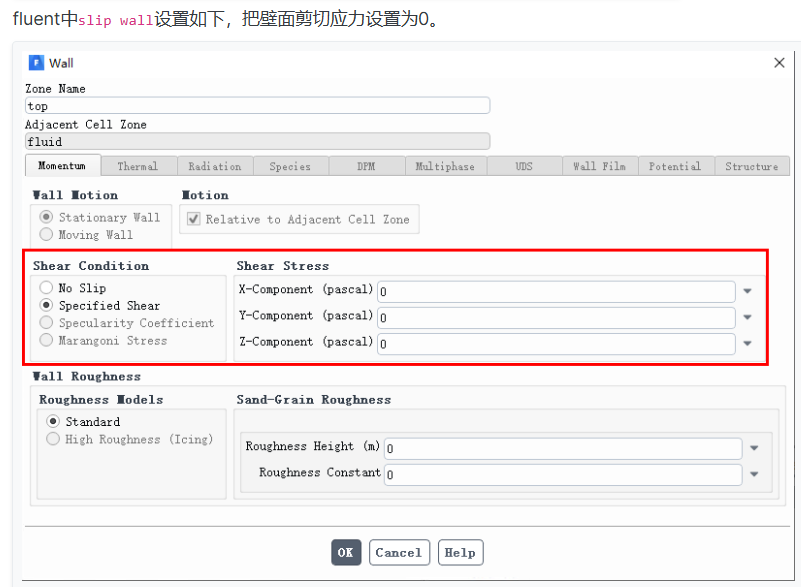
滑移壁面边界条件@齐彦鹏
滑移壁面,剪切应力设置为0
-
周期性边界明渠的两点相关性分析Ruu、Rvv、Rww如何计算?@coolhhh
#5 的方法2下面公式是指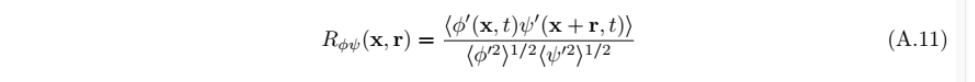
-
周期性边界明渠的两点相关性分析Ruu、Rvv、Rww如何计算?- 这两个图分别对应 方法1 和 方法2 的计算结果吗,还是不同方向的结果?
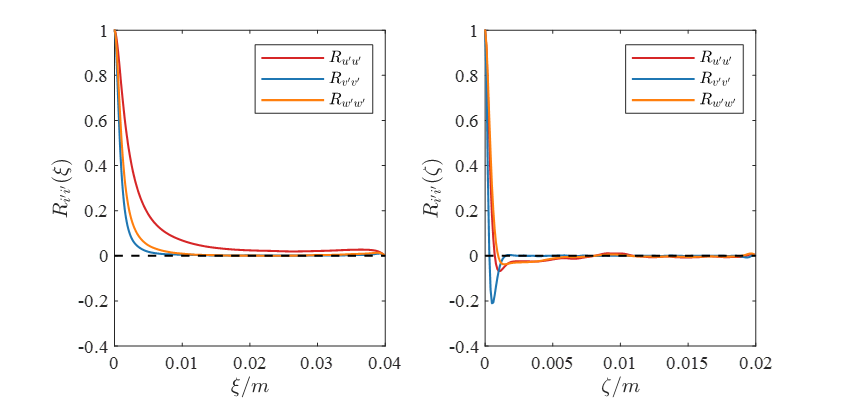
- 对于方法1 ,这个写法是系综平均求相关函数,最后还要归一化得到相关系数。如果时间非平稳和空间非均匀,理论上统计量跟选择的参考点位置
x和时间t都相关。但槽道流的在展向和顺流向是均匀+时间平稳的,所以最后的统计特性都与参考位置参考点位置x和时间t都无关,所以可以用空间和时间一起平均得到最终统计量,of自带的postChannel工具就是这么做的。
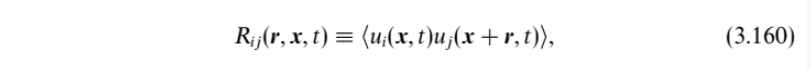
- 计算空间相关函数有2种方法:
(1)方法1,根据《Shin K, Hammond J. Fundamentals of signal processing for sound and vibration engineers[M]. England: John Wiley & Sons, 2008.》,已知在固定点位置,一条时间序列u(x=x0, y=y0, z=z0, t),针对这条时间序列求时间相关函数公式如下截图,在MATLAB中对应函数是xcorr。这种方法要求序列足够长,并且点数足够多,才能算的准确。

类似的,在某一固定时刻,沿着空间展向z的一条空间序列
u(x=x0, y=y0, z, t=t0),也一样可以用xcorr求空间相关函数,计算结果要准确,就要求这条序列的展向宽度要足够大,且点数足够多,否则计算结果就会偏差大。 如果计算域纵向足够长,把每条展向空间相关函数做空间平均,得到的结果应该也会比较准确。想要更准确就要加上每个时刻的平均,就要输出每个时刻的数据,计算量太大了,用空间平均了,其实时间平均应该就不用了,结果差别不会太大。(2)方法2,跟下面公式一样,计算两个序列的相关系数,对应MATLAB函数
corrcoef。已知展向上空间多个点A(x0, y0, zA, t)、B(x0, y0, zB, t)、C(x0, y0, zC, t)的时间序列,就可以假设选定A为参考点,依次计算出 AB、AC的相关系数,然后就可以把连成展向空间相关系数曲线。这种方法就要设置展向监测点,测量出每个点的时程数据,相对来说时程数据比空间数据(受限于计算域大小)更长,计算结果应该会比较准确。还可以设置多个不同x向位置的测点,再对计算的空间相关系数曲线平均,结果会更准确。 -
LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+? -
Wray-Agarwal湍流模型@wangfei9088 感谢大佬


-
Wray-Agarwal湍流模型@wangfei9088 大佬,按照这种方式自定义湍流模型,会提示
Duplicate entry的警告,直接忽略就可以吗?这个帖子提到不要有这种警告,就要复制很多文件,感觉挺麻烦Duplicate entry laminar in runtime selection table incompressibleMomentumTransportModel #0 /home/install/OpenFOAM/OpenFOAM-10/platforms/linux64GccDPInt32Opt/lib/libOpenFOAM.so(_ZN4Foam5error14safePrintStackERSo+0x32) [0x7f0a93735072] -
LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+?系数B确实会随着雷诺数不同,有略微波动。《Kim J, Moin P, Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number[J]. Journal of fluid mechanics, 1987,177:133-166.》文章中也提到了雷诺数比较低,B=5.5

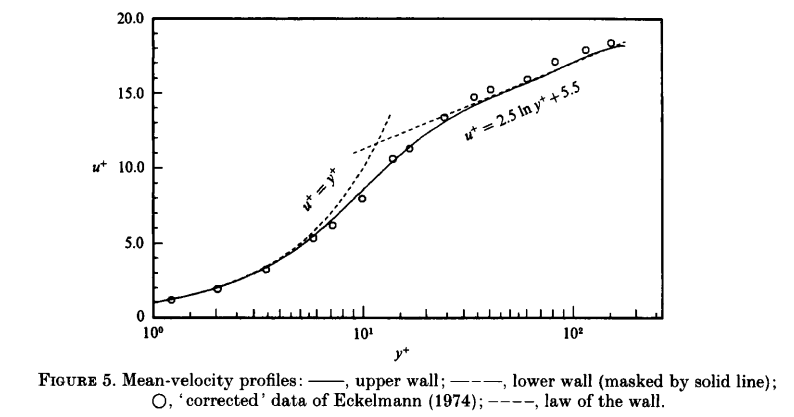
《Moin P, Kim J. Numerical investigation of turbulent channel flow[J]. Journal of fluid mechanics, 1982,118:341-377.》中的结果 B=5.0
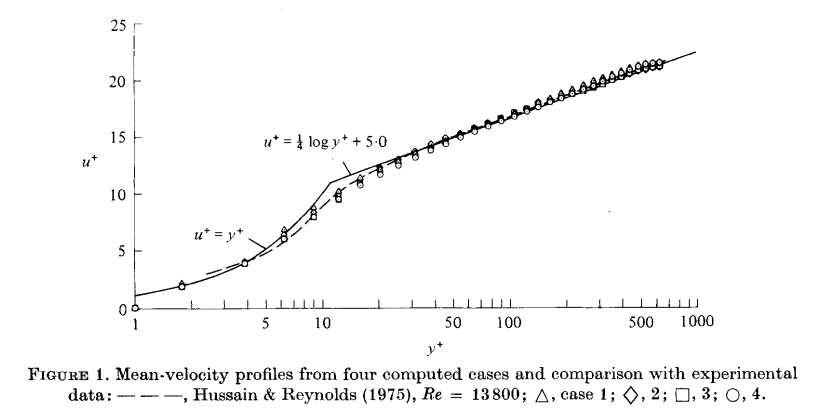
-
LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+?我对 https://turbulence.oden.utexas.edu/ 提供的
Channel Data (2015)不同雷诺数湍流的 y+U+ 的对数律系数拟合了下,主要是对y+范围30-300这段进行拟合(考虑过高的y+段对拟合结果有挺大影响)。约翰霍普金斯数据库的 $Re_\tau=1000$和$Re_\tau=5200$也是来自于这个数据库。由于考虑拟合段不同,所以本次拟合结果的系数与约翰霍普金斯数据库提供的系数有点不同。以下是拟合结果,可以看出DNS计算结果,只有$Re_\tau=180$满足系数$\kappa=0.4,\ -C=5.5$,其他雷诺数结果其实都有点偏差
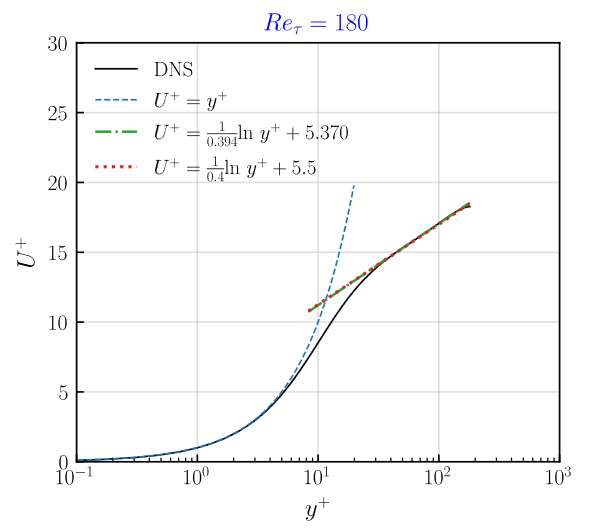
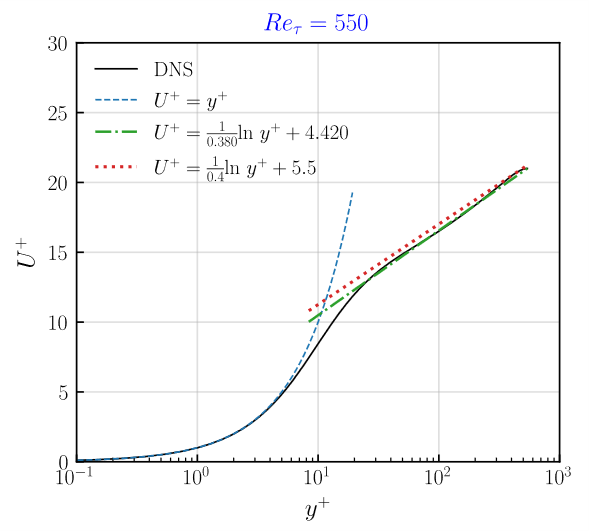
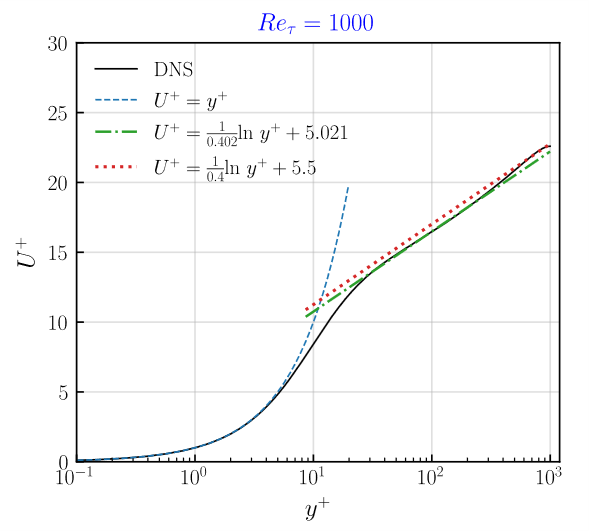
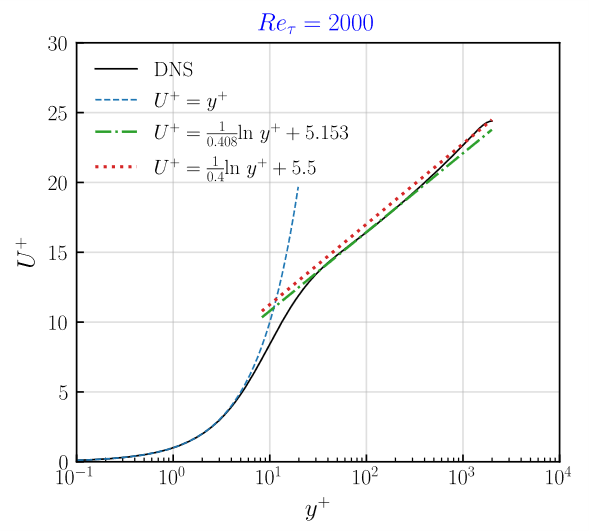
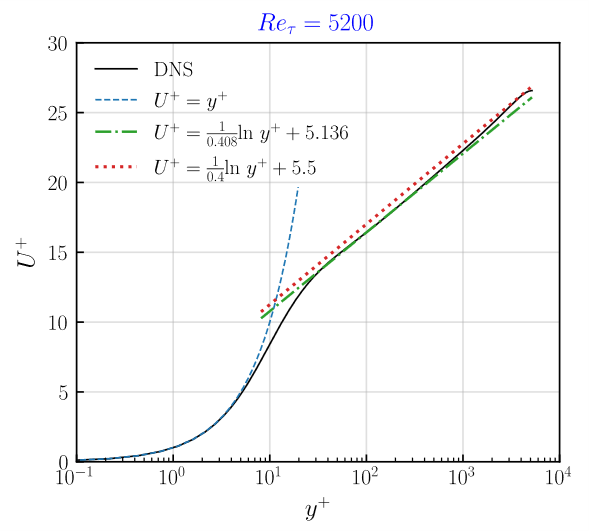
-
LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+?@学流体的小明 感谢回复

-
LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+?- 分辨率会影响结果,channel395的分辨率确实比较差。
- 但看约翰霍普金斯湍流数据库$Re_\tau=1000$的结果,拟合的是$\kappa=0.4098,\ -C=5.2$。以及$Re_\tau=5200$,拟合的是$\kappa=0.384,\ -C=4.27$,说明对于不同雷诺数,这个对数律系数是波动的。
https://turbulence.pha.jhu.edu/docs/README-CHANNEL5200.pdf

- 还有个问题是网格分辨率足够情况下,摩擦雷诺数1000和550的工况,最终模拟的$u_\tau$与理论值有对得上吗?计算$U^+$和$y^+$用的实际的$u_\tau$,还是理论的$u_\tau$?
-
LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+?也就7#用实际计算的$u_\tau$计算的这个图,需要改变对数律的公式系数

-
LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+?根据《无痛苦NS方程笔记》,对数率公式是有个E系数,一般取9.8。《An introduction to computational fluid dynamics: the finite volume method》也是这种写法。

约翰霍普金斯湍流数据库$Re_\tau=1000$结果,包括上文对$Re_\tau=395$结果对数律对比,都是将
E=1来考虑。https://turbulence.pha.jhu.edu/docs/README-CHANNEL.pdf

- 为什么最终画图时候,对数率都取
E=1,而不用E=9.8? - 根据约翰霍普金斯湍流数据库,DNS计算$Re_\tau=1000$的对数律,其 k 和 C 值并不是取 $\kappa=0.4, -C=5.5$。换句话说,光滑壁面的对数律系数,是否会随着雷诺数的改变而改变,而不是都是固定的值$\kappa=0.4, -C=5.5$?
- 现在有个观点是,of自带算例 channel395,后处理计算$U^+$和$y^+$时,应该用实际计算出来的$u_\tau$,而不能用理论$Re_\tau=395$的反算值。原因是自带算例 channel395 实际模拟得到的$Re_\tau$并不等于395,相当于实际得到的是其他雷诺数的充分发展湍流,用模拟的$u_\tau$计算$U^+$和$y^+$,其剖面在粘性子层依然满足线性关系,但在对数律上公式系数应当类似约翰霍普金斯湍流数据库$Re_\tau=1000$结果重新取值,使得满足另外的对数律关系,而不是沿用$\kappa=0.4, -C=5.5$
- 为什么最终画图时候,对数率都取
-
mesh_.C()[celli]编译报错@liujm 试了下确实没问题,
mesh.C()[celli]效果跟mesh.C().primitiveField()[celli]效果是一样的。#include "fvCFD.H" int main(int argc, char *argv[]) { #include "setRootCase.H" #include "createTime.H" #include "createMesh.H" label celli = 0; const vector cellCentre = mesh.C()[celli]; const vector cellCentre2 = mesh.C().primitiveField()[celli]; Info << "cellCentre = " << cellCentre << endl; Info << "cellCentre2 = " << cellCentre2 << endl; Info<< "End\n" << endl; return 0; } -
如何在controlDict中创建一个场,不需要修改求解器OpenFOAM-v2206/tutorials/incompressible/pimpleFoam/LES/planeChannel/setups.orig/common/system/controlDict,有一个计算Cf场的函数,可以参考下:Cf { type coded; libs (utilityFunctionObjects); name Cf; timeStart $/timeStart; writeControl writeTime; codeExecute #{ auto* CfPtr = mesh().getObjectPtr<volScalarField>("Cf"); if (!CfPtr) { Info<< "Create skin-friction coefficient field" << nl; CfPtr = new volScalarField ( IOobject ( "Cf", mesh().time().timeName(), mesh(), IOobject::NO_READ, IOobject::AUTO_WRITE ), mesh(), dimless ); regIOobject::store(CfPtr); } auto& Cf = *CfPtr; Info<< "Computing skin-friction coefficient field\n" << endl; const auto& tau = mesh().lookupObject<volVectorField>("wallShearStress"); const dimensionedScalar Ubulk(dimVelocity, 17.55); Cf = mag(tau.component(0))/(0.5*sqr(Ubulk)); #}; } -
mesh_.C()[celli]编译报错 -
Smagorinsky模型系数问题最近看《Holzmann T. Mathematics, numerics, derivations and OpenFOAM》,里边也提到大部分情况忽略k,对结果影响不大:



