CFD中文网

@李东岳 不好意思李老师，中间去做了一些别的工作，没有怎么学习of，最近又回头看了一下这个代码，用这个方法和of的动网格oscillatingRotatingMotion计算了同一个工况，结果还是显示在相同的振幅和频率下，惯性力不能像动网格一样使液舱出现明显的晃荡现象。感觉在液舱尺度是实验缩尺尺度下，惯性力也不是很大

@李东岳 李老师我重新检查了一下，之前bf是在求解UEqn时加入的，现在改成把rho*bf放在了方程UEqn里面。

bf=(angulara^rotateR) + (angularv^(angularv^rotateR))+(2*angularv^U);
fvVectorMatrix UEqn
(
    fvm::ddt(rho, U)
  + fvm::div(rhoPhi, U)
  - fvm::Sp(fvc::ddt(rho) + fvc::div(rhoPhi), U)
  + turbulence->divDevRhoReff(rho, U)
  -rho*bf     //加在这里了                                                       
);

直接算还是不行，然后尝试在算例中关掉了重力

dimensions   [0 1 -2 0 0 0 0];
value             (0 0 0);

这时候有晃荡现象了

是因为重力作用抵消了惯性力的作用吗？
现在的模型没有表面张力系数sigema给的是0，使用的是层流laminar，和真实的横摇运动还有一定差距，请问李老师还有什么改进的建议吗 ？

@李东岳 在 关于晃荡惯性力的植入 中说：

$$
\begin{array}{l}
\mathbf{F}_y(t)=-\rho\left(g \sin \theta(t)+y \omega(t)^2+z \varepsilon(t)+2 \omega(t) u_y(t)\right) \boldsymbol{j} \\
\mathbf{F}_z(t)=-\rho\left(g \cos \theta(t)+z \omega(t)^2-y \varepsilon(t)-2 \omega(t) u_z(t)\right) \boldsymbol{k}
\end{array}
$$

这个方程里面非粗体的$\omega,\varepsilon$以及$\theta_m,T$你知道是什么么

老师我的理解是，$\omega,\varepsilon$是标量表示的角速度和角加速度，文章里是把惯性力以分量的形式添加的，openfoam里的动量方程是矢量方程，我就直接把角速度和角加速度写成矢量，把惯性力直接加到方程里了，没有将其分解到y轴和z轴上。

@李东岳 在 关于晃荡惯性力的植入 中说：

在循环前植入：

我忽然注意到你写的这个。你要在循环中更新一下这个量。你更新没有。

之前没有更新，我在UEqn.H文件的开头又加了一行：

bf=(angulara^rotateR) + (angularv^(angularv^rotateR))+(2*angularv^U);

但是算出来后的结果还是像上面的图那样

@李东岳 李老师您好！epsilon是液舱晃荡的角加速度，omega是液舱晃荡的角速度，ur是相对于液舱的速度，也就是以液舱为参考系的速度。

原文：
1-s2.0-S0360544223003298-main.pdf

各位大佬好
本人openfoam小白，最近在学习液舱晃荡相关算例，想不使用动网格，通过在动量方程中添加惯性力实现晃荡，惯性力类似：


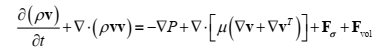
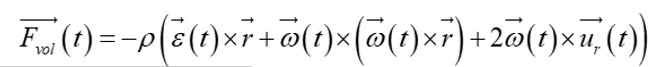
在循环前植入：

IOdictionary bodyForceProperties
(
    IOobject
    (
        "bodyForceProperties",
        runTime.constant(),
        mesh,
        IOobject::MUST_READ_IF_MODIFIED,
        IOobject::NO_WRITE
    )
);
//幅值输入
dimensionedScalar theta0_
(
    "theta0_",
    dimless,
    bodyForceProperties
);
//频率输入
dimensionedVector omega0_
(
    "omega0_",
    dimensionSet(0,0,-1,0,0,0,0),  //给量纲
    bodyForceProperties
);


//液面高度输入
dimensionedScalar freesurfacez
(   "freesurfacez", 
    dimLength, 
    bodyForceProperties
);
const Time& time_ = mesh.time();
scalar t = time_.value();
vector omega0 = omega0_.value();
scalar magomega0 = mag(omega0);
scalar theta0 = theta0_.value();
volVectorField rotateR = mesh.C();  
forAll(rotateR,celli)
{
   rotateR[celli].x() = 0.0;
   rotateR[celli].z() += freesurfacez.value();  //相当于绕y=0，z=-自由液面高度的轴旋转
}
dimensionedVector angulara //旋转角加速度
(
   "angulara",
    dimensionSet(0,0,-2,0,0,0,0),  
    -omega0*magomega0*theta0*std::sin(magomega0*t)
);
dimensionedVector angularv //旋转角速度
(
    "angularv",
    dimensionSet(0,0,-1,0,0,0,0),  
    omega0*theta0*std::cos(magomega0*t)
);
volVectorField bf
(
    IOobject
    (
       "bf",
        runTime.timeName(),
        mesh,
        IOobject::NO_READ,
        IOobject::AUTO_WRITE
    ),
    (angulara^rotateR) + (angularv^(angularv^rotateR))+(2*angularv^U)
);

其中bf为惯性力，再将惯性力加到动量方程中：

if (pimple.momentumPredictor())
{
    solve
    (
        UEqn
     ==
        fvc::reconstruct
        (
            (
                interface.surfaceTensionForce()  
              - ghf*fvc::snGrad(rho)
              - fvc::snGrad(p_rgh)               
            ) * mesh.magSf(）
        )-bf
    );
}

算了一个30°，角频率1的算例，结果是这样的

请问各位大佬问题出在哪里？