CFD中文网

@Afr1yne
如果是算外流场，应该 NASA 建议的那样来设置 nuTilda 的入口边界条件。log中这样的 bounding 没关系的，不会影响结果。
另：看你的 log，你用的是 PISO 模式，但是不开启 momentumPredictor ？这样似乎不是一个很好的选择。

首先，对于压力方程，因为其只有 laplacian项，所以可以推导出来这样的压力方程的系数满足 “网格单元对应的对角矩阵系数等于其余影响的单元系数之负和” 这个特点。
其次，我们来看 setReference 这个函数做了什么。查看 fvMatrix 类中 setReference 函数的实现，如下：

template<class Type>
void Foam::fvMatrix<Type>::setReference
(
    const label celli,
    const Type& value,
    const bool forceReference
)
{
    if ((forceReference || psi_.needReference()) && celli >= 0)
    {
        source()[celli] += diag()[celli]*value;
        diag()[celli] += diag()[celli];
    }
}

可以看到，这个函数确实是把对应网格的对角元素值翻倍了。 setReference 函数的目的是把指定网格（对应参数 celli）的值设置为指定的值（对应参数 value），可以为什么这样实现就可以达到这个目的呢？原理如下：

在不可压缩流体计算中，我们求解的是压力泊松方程（Pressure Poisson Equation），它通常形如：
$$ \nabla \cdot (\frac{1}{A_p} \nabla p) = \nabla \cdot (\frac{H(\mathbf{U})}{A_p}) $$
这里 p 是压力，A_p 是速度方程离散后中心网格的系数，H(U) 是一个与速度相关的项。

当我们将这个方程离散化后，会得到一个大型的线性方程组：
$$ \mathbf{A} \mathbf{p} = \mathbf{b} $$
其中 A 是系数矩阵，p 是我们要求解的、包含所有网格压力的向量，b 是源项向量。

关键问题：如果计算域的所有边界都是第二类边界条件（Neumann BC），比如 zeroGradient（法向梯度为零），这意味着我们只规定了压力的梯度，而没有规定压力的绝对值。

从物理上讲，不可压缩流的压力是相对的。如果 p 是一个有效的解，那么 p + C（其中 C 是任意常数）也同样是一个有效的解，因为它不会改变压力的梯度（∇(p+C) = ∇p）。

因此，我们必须通过指定一个点的压力值来消除这种不确定性，为整个压力场提供一个“锚点”或“基准”。
setReference 的目标是强制让某个特定网格 celli 的压力 p[celli] 在求解后等于我们设定的参考值 value。
也就是说，我们想让方程组的解满足：
$$ p_{\text{celli}} = \text{value} $$

3. 代码实现与数学原理剖析

我们再来看这两行代码，并结合线性方程组 Ap=b 在第 celli 行的具体形式来分析。

对于网格 celli，其对应的线性方程（未修改前）是：
$$ A_{ii} p_i + \sum_{j \in N(i)} A_{ij} p_j = b_i $$
其中：

• i 就是 celli
• p_i 是网格 i 的压力
• A_{ii} 是对角线元素，对应 OpenFOAM 代码中的 diag()[celli]
• A_{ij} 是非对角线元素，表示网格 i 与其邻居网格 j 的相互影响
• b_i 是源项，对应 source()[celli]

现在我们来分析这两行代码对这个方程做了什么修改：

核心代码:

source()[celli] += diag()[celli]*value;
diag()[celli] += diag()[celli];

第一步：source()[celli] += diag()[celli]*value;

这行代码修改了源项 b_i。修改后的新源项 b'_i 为：
$$ b_i^{'} = b_i + A_{ii} \cdot \text{value} $$
此时，方程变为：
$$ A_{ii} p_i + \sum_{j \in N(i)} A_{ij} p_j = b_i + A_{ii} \cdot \text{value} $$

第二步：diag()[celli] += diag()[celli];

这行代码修改了对角线元素 A_{ii}。修改后的新对角线元素 A'_{ii} 为：
$$ A_{ii}^{\prime} = A_{ii} + A_{ii} = 2A_{ii} $$
现在，第 i 行的方程最终变成了：
$$ (2A_{ii}) p_i + \sum_{j \in N(i)} A_{ij} p_j = b_i + A_{ii} \cdot \text{value} $$

让我们来整理一下这个修改后的方程。我们可以把 (2A_{ii}) p_i 拆开：
$$ (A_{ii} p_i + \sum_{j \in N(i)} A_{ij} p_j) + A_{ii} p_i = b_i + A_{ii} \cdot \text{value} $$

也就是说，当调用了 setReference 函数后，求解的线性方程组发生了变化。通过求解这个修改后的方程，能让方程趋于收敛到 $p_i = \text{value}$ 这个解，此时
$$ A_{ii} p_i = A_{ii} \cdot \text{value} $$
因此也会使得修改前的
$$ A_{ii} p_i + \sum_{j \in N(i)} A_{ij} p_j \approx b_i $$
也同时成立。

通过这样就实现了让指定的网格的解等于指定值，同时又不违反从 Laplacian 项离散后得到的方程。

@Afr1yne 这都能翻出来，服了。我回去给你发

@2514717616 你的 codedFixedValue 图片中的
(*this)[faceI] = vector(Umax-(y-H)*(y-H)), 0, 0); 这一行的等号右边括号都没匹配对。多了一个 ")"

@ChangranLv
你这个曲线有一个明显的规律：网格越多，中心速度就越小。很大一个可能性是你的计算根本没有收敛。用simpleFoam 求解稳态问题，网格越多收敛会越慢，需要越多迭代步。

@李东岳 pvserver 并行运行在后端，paraview远程连上去。相当于计算密集的操作都在后端服务器上跑，paraview 只是当个显示图片的界面来用。

@火山口玩泥巴 不需要，paraview本身只能用1个核。

你这个算例有几处不太合理的地方：

1. 估计你的网格是边界层首层厚度很小的那种吧，那么你用 standard k epsilon 这个湍流模型是不合适的，建议使用 kOmegaSST。
2. 抛开 k-epsilon 模型的合理性不谈，你这个 k epsilon nut 的 Inlet 边界条件设置也是不合理的。首先，你的入口速度是 9m/s，k 的 Inlet 值为 0.375，意味着入口湍流度为约 5.5%，这个值是偏大的。而 epsilon 的如何值为 0.07，意味着入口的 nut 值为 0.09*0.375^2/0.07=0.1808，超过流体粘度的 10000倍，这个是严重偏大的值。

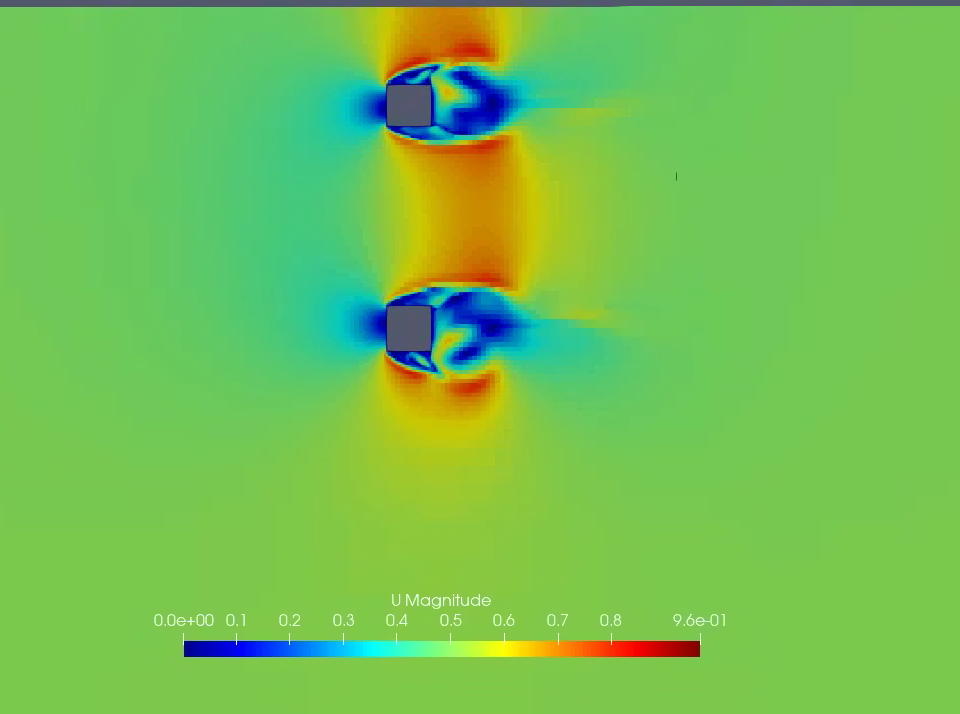
用你1楼提供的算例运行，发现在 subsetMesh这一步之后，得到的 frame 边界的 type 是 empty，并且 0 文件里面 U，p 场的 frame 边界的边界条件也变成了 empty。所以，之后的计算你这个 frame 边界都是以 empty 边界条件在运行，结果肯定就完全错了。
解决办法：在 subsetMesh 这一步之后把0文件里面那些场的边界条件修改过来，改成正确的设置再重新计算。
跑了几步，结果如下：

@旺财R @HIT_lly @youhaoyu @1064168551 已发

@bit_hypersonic
cellLimited 这个东西是一种 gradient limiter，你可以搜一下这个关键字了解一下其物理含义。也可以参考如下论文看看：Michalak, K., & Ollivier-Gooch, C. (2008). Limiters for unstructured higher-order accurate solutions of the euler equations. 46th AIAA Aerospace Sciences Meeting and Exhibit, January. https://doi.org/10.2514/6.2008-776

@Joker

1. 会使用设置的厚度，也就是说，二维算例 z 方向设置不同的厚度，虽然对流场没影响，但是会影响 force 算出来的力的值
2. 力的单位是 N，OpenFOAM 里面默认所有的单位都是 SI 量纲组成的单位。

@东方白杨 有一个 functionObject 叫 columnAverage，可以实现对一个方向进行平均。

@z597288 3楼用到的几个命令组合一下应该可以实现

可以用 LaTex 的语法来实现希腊字母输入。

k 和 epsilon 可以也设置为 slip，nut 设置为 calculated。

切完之后再用 clip ，或者 先用 Select Cells Through，选定你想显示的网格，再用 extract selection 把选定的网格提取出来单独显示即可。

1. 你的背景网格三个方向的尺寸差异太大了，z方向的尺寸只有其他两个方向的大概 1/6，这不利于 snap 。建议将背景网格尺寸调成一样，或者至少把差异缩小试试。
2. snap 阶段建议增加 featureSnap 的次数
3. meshQuality里面，maxNonOrtho 你设置的是45，建议调大一些，比如调到65。

试了一下，不完美，但是有改善。

这段代码跟使用SA湍流模型计算有一个差异是：这段代码是先求解 nuTilda 方程得到 nut，然后再用更新的nut来构建和求解 UEqn，而直接使用湍流模型的时候是先求解 UEqn，pEqn，然后再用修正的速度来构建和求解nuTildaEqn

@myheart OpenFOAM 里面求解理想气体（ideal gas，无粘性）流动的求解器是 rhoCentralFoam，你看这个求解器的算例壁面都用的是某种滑移边界。