CFD中文网

三维的类似情况，我最后一个打错字了。

你理解错了，xyz只是一个下标而已。如果是二维情况，就只有cz，表示c是垂直于xy平面（平行于z轴）的矢量。其余两个是三位的类似情况而已

啊？大C不是公式19下面那行文字定义的吗？

小c和大C量纲是一致的。它们都是旋转速度啊，量纲都是1/s。C只是c的一个扩展而已，包括了三个方向的旋转角速度分量

原文方程4的力矩计算，是叉乘计算，力矩是有方向的。因此有另外的符号变化，原文是对的。

如果流场稳定了，openfoam计算的那项，应该也不起作用了吧。

@李东岳 角动量与C成正比，它在时间上的导数就是受到的力矩，这里面写了粘性力矩; 压力应该没有力矩，因为是势能。另外套上了对流项，建立的方程

@李东岳 感谢。希望能得到更多人的鉴定

看了一篇论文，观点非常新颖，认为NS方程用于CFD有角动量损失的缺陷。全文逻辑严密，有理论分析且给出解决方案。通过仿真计算，揭示传统方法损失了角动量，而新方法克服了角动量损失问题。甚至理论推导了传统方法角动量损失的大小，并且与数值仿真结果高度匹配！由于其观点挑战常识，因此发帖请教各高手鉴定。

1.理论依据
众所周知，相对于角动量，NS方程是平动量方程。那么在NS方程控制的流场里，如何确保流动是符合角动量守恒的呢。论文表示，经典理论是利用本构方程实现的：本构方程的建立条件就是，假定了无限小物质的表面是力矩平衡的。通过在NS方程的粘性项中引入本构方程，从而确保角动量的守恒（平衡的力矩不改变角动量）。
但是论文很快又指出，多数时候用于CFD的简化版NS方程，其中的本构方程在简化过程中被消去了。因此，简版NS方程不含本构方程，模拟出的流场是不满足角动量守恒定律的！
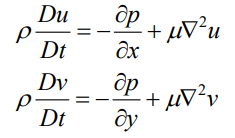=========简化的NS方程

2.解决方案
为了克服这个问题，论文在二维情况下给出了新解决方案，通过增加一个角动量方程以确保角动量守恒。具体方法此处省略。

3.效果展示
论文做了简单的对比模拟计算。证明常规方法计算结果确实有力矩不平衡的问题（角动量不守恒），文中提供的新方法克服了这个问题，而且给出的流场分布有所不同。更让人惊奇的是，论文理论推导给出了NS方程流场残余力矩的大小（“等于粘性系数与流场涡环量的乘积”），与数值模拟结果符合很好！

由于论文过于奇葩，特向各老师请教，如何评价这个论文。
论文链接在此 https://pan.baidu.com/s/1yrucFbevfpb1QLjX2Hl0qw?pwd=qatp
无法下载的留言邮箱，看见了会发过去。