简版NS方程用于CFD有完备性问题？这篇论文有看法
-
看了一篇论文，观点非常新颖，认为NS方程用于CFD有角动量损失的缺陷。全文逻辑严密，有理论分析且给出解决方案。通过仿真计算，揭示传统方法损失了角动量，而新方法克服了角动量损失问题。甚至理论推导了传统方法角动量损失的大小，并且与数值仿真结果高度匹配！由于其观点挑战常识，因此发帖请教各高手鉴定。
1.理论依据
众所周知，相对于角动量，NS方程是平动量方程。那么在NS方程控制的流场里，如何确保流动是符合角动量守恒的呢。论文表示，经典理论是利用本构方程实现的：本构方程的建立条件就是，假定了无限小物质的表面是力矩平衡的。通过在NS方程的粘性项中引入本构方程，从而确保角动量的守恒（平衡的力矩不改变角动量）。
但是论文很快又指出，多数时候用于CFD的简化版NS方程，其中的本构方程在简化过程中被消去了。因此，简版NS方程不含本构方程，模拟出的流场是不满足角动量守恒定律的！
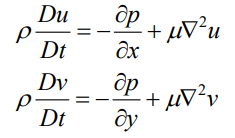=========简化的NS方程2.解决方案
为了克服这个问题，论文在二维情况下给出了新解决方案，通过增加一个角动量方程以确保角动量守恒。具体方法此处省略。3.效果展示
论文做了简单的对比模拟计算。证明常规方法计算结果确实有力矩不平衡的问题（角动量不守恒），文中提供的新方法克服了这个问题，而且给出的流场分布有所不同。更让人惊奇的是，论文理论推导给出了NS方程流场残余力矩的大小（“等于粘性系数与流场涡环量的乘积”），与数值模拟结果符合很好！由于论文过于奇葩，特向各老师请教，如何评价这个论文。
论文链接在此 https://pan.baidu.com/s/1yrucFbevfpb1QLjX2Hl0qw?pwd=qatp
无法下载的留言邮箱，看见了会发过去。 -
我详细看了一下：
-
首先原文的方程2的$\Lambda$和$\Lambda^T$与常规的$\nabla\bfU^T$以及$\nabla\bfU$不一致。这里面牵涉到分子布局与分母布局
-
正常来说虽然理论上$\nabla\cdot(\nu\nabla\bfU^T)=0$，但OpenFOAM都进行了求解，并没有直接省略掉
-
原文方程4我觉得他的符号写反了，应该是：$(-0.5)... + 0.5... +(-0.5) + 0.5...$，如果这样写的话方程4=0
这个论文的根本是认为NS方程不满足角动量守恒。我把推导更新到《无痛苦ns方程笔记》第
NS方程的角动量守恒一节了。 -
-
确实。
但是那个量纲不一致。c的单位是$\frac{1}{ s}$，C的单位是$\frac{1}{m\cdot s}$，$\nabla\times C$的单位是$\frac{1}{m^2\cdot s}$。$\nabla^2\bfU$的单位是$\frac{1}{m\cdot s}$。
$\frac{1}{m\cdot s}\neq\frac{1}{m^2\cdot s}$。OpenFOAM计算时候报错了。
如果流场稳定了，openfoam计算的那项，应该也不起作用了吧。
这个$\bfU$和$\bfU^T$的贡献一个在切向一个在法向。还约不下去。
