@李东岳 李老师能帮我提供一个大致的方向么 我现在不知道该往哪个方向使劲儿了
我现在不知道该往哪个方向使劲儿了
阿飞
帖子
-
空泡溃灭局部质量守恒方法 -
空泡溃灭局部质量守恒方法在使用compressibleInterFoam求解器计算单空泡溃灭时,会遇到质量不守恒的问题。相关论文中的处理方式是假设质量均匀分布在整个空泡内,在每一步计算时对密度场进行修正,如下式所示:

公式很好理解,每一个时间步计算气相质量,并与初始气相质量进行比较,将比值与当前密度场相乘得到新的密度场。
这一方法已经成功实现。
参考文献:Max Koch. Numerical modelling of cavitation bubbles with the Finite Volume method. (https://doi.org/10.25625/JVCJVW)该作者2020年发表的PHD论文中提出了一种新的质量修正方法:局部质量修正法,如下所示:

这种方法计算了气相的质量守恒方程,但在求解该方程的过程中,计算结果显示质量并不守恒,反而越来越少。就这一问题我向作者发送了邮件询问,得到作者的回复:式中alpha_g必须声明为IOobject-VolScalarField,在0.001处截断,最后更新所有相关物理量。但是仍旧没有得到正确的结果,无法实现预期的质量守恒功能。
参考文献:Max Koch. Laser cavitation bubbles at objects: Merging numerical and experimental methods.
我想咨询一下各位老师,这样的方程我用如下形式求解是否正确:surfaceScalarField phiAlpha2=fvc::interpolate(alpha2_Tilde)*phi; solve(fvm::ddt(alpha2_Tilde,rho2)+fvm::div(phiAlpha2,rho2)); -
compressibleInterFoam计算气泡溃灭已解决:使用foam-extend4.1版本中的compressibleInterFoam求解器,模型修改为球对称模型,计算正确。
P.S. foam-extend4.1中的compressibleInterFoam没有耦合温度方程,计算过程中没有出现上述问题。
参考文献:Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM -
compressibleInterFoam计算气泡溃灭@李东岳 感谢李东岳老师的回复,我尝试去研究一下,后续有什么进展会发上来的。




-
compressibleInterFoam计算气泡溃灭想请问一下各位老师,使用compressibleInterFoam计算单气泡溃灭时,能量方程发散是因为什么原因呢?
1、OpenFOAM版本:OpenFOAM v2006
2、计算模型:二维轴对称模型

3、边界条件:模型有四个边界,其中有两个是wedge边界,有一个是empty边界(对称轴),剩下的一个就是远场边界。对于远场边界,alpha:zeroGradient p_rgh:fixedFluxPressure U:noSlip
上述边界中,速度边界是论文中给出的。其余边界尝试过使用totalPressure、inletOutlet、pressureInletOutletVelocity,对计算结果没有太大的影响。
4、热物理模型:气体采用理想气体模型,液体采用Tammann状态方程
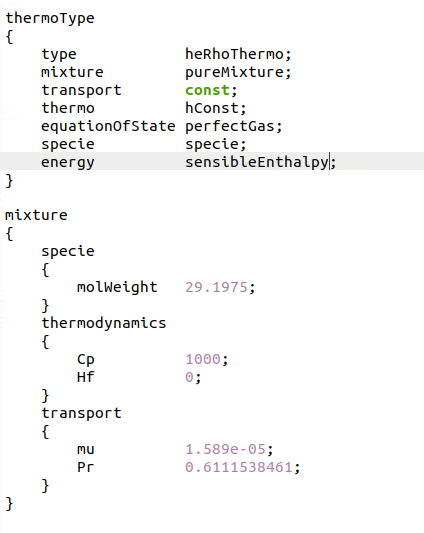
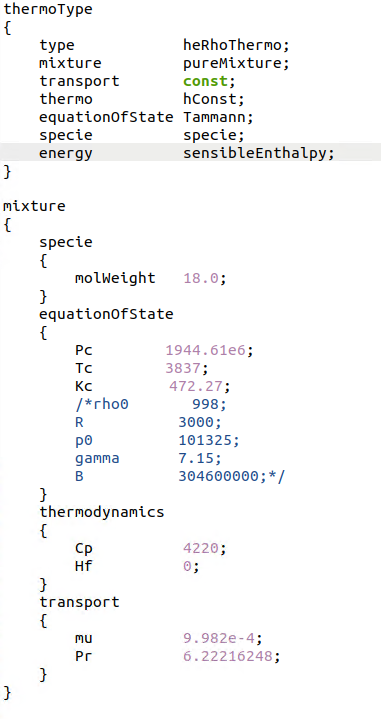
经过检验,液体采用perfectFluid状态方程同样会使得能量方程发散。
5、初始条件:初始化气泡半径747微米,10Pa,293.15K。周围液相环境:101325Pa、293.15K。以上就是主要的设置内容,仿真在计算到6.2e-5s时,能量方程突然发散,提示负温度。查看此时的云图发现如下现象:

相分数图中边界模糊,且此部分压力场与速度场非常奇怪,出现这样的原因时网格的问题吗?

6、以上仿真内容是尝试更改pMin参数得来的。pMin参数如果按照默认值1e4可以一直计算求解器不会崩溃,单结果与论文相去甚远。以上仿真是将pMin参数更改为10得到的结果,实在找不到原因是什么了,请各位老师帮忙指导一下!
P.S. 前期已经调研过能量方程发散的原因,可能是因为网格问题、时间步长、边界条件不适当、初始条件问题。
网格已经经过一次加密、库朗数也维持在0.1左右、边界条件因为很简单可调整空间不大、初始条件是论文中给出的数据。 -
关于绝热状态方程熵的计算过程OpenFOAM v2006中,adiabaticPerfectFluid状态方程如下:
$\rho (p)=\rho_{ref}(\frac{p+B}{p_{ref}+B})^{\frac{1}{n_{T}}}$
根据熵的计算公式:
$dS=c_{p}\frac{dT}{T}-(\frac{\partial v}{\partial T})_{p}dp$
求解器中将这一公式分为两部分进行积分计算,其中第一部分$c_{p}\frac{dT}{T}$ 的积分计算在thermophysicalModels/specie/thermo/hConst/hConstThermoI.H中实现,即$c_{p}*log(\frac{T}{T_{std}})$
但第二部分的积分,由于公式是绝热状态的,没有温度作为参数,想请教一下官方求解器中为什么会进行以下处理:通过源代码公式的求导反推,官方求解器在计算第二部分积分时,在状态方程的分母上直接添加了温度T,如下式:
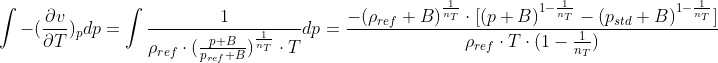
公式源代码详见adiabaticPerfectFluidI.H文件的S函数:template<class Specie> inline Foam::scalar Foam::adiabaticperfectFluid<specie>::S ( scalar p, scalar T ) const { scalar n=1-1.0/gamma_; return -pow(p0_+B_,1.0/gamma_)*(pow((p+B_),n)-pow((Pstd+B_),n)) /(rho0_*T*n); }除上述绝热状态方程外,线性变化的状态方程linear也采用了同样的处理方式,想知道为什么可以这样处理?
另外一个问题是,如果采用上述处理之后,对于气体的$c_{p}-c_{v}$,根据公式:
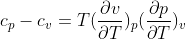 该如何处理?
该如何处理? -
虚拟机计算扩容问题直接虚拟机扩充磁盘空间,在Ubuntu里用gparted管理磁盘
