拉格朗日中的湍流分散力模型
-
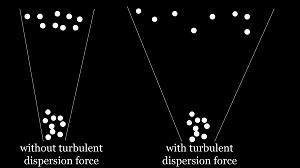
算法背景
湍流分散力:Turbulent dispersion force
湍流的作用会导致粒子产生分散作用。但对于不同的研究体系,湍流分散力的作用并不相同。如果考虑湍流分散力的作用,拉格朗日模型和欧拉模型中的处理方式并不一致。
-
拉格朗日模型中的Turbulent Dispersion一般都用的是随机行走模型,如Stochastic tracking model
-
欧拉欧拉模型中的Turbulent Dispersion一般用力/每单位体积来描述,具体的细分为某些模型如lopezDeBertodano model或者Burns model
这种湍流分散力的处理方式不一致主要取决于介尺度模型中的粒子直接跟踪算法和宏观模型中N-S方程中的动量方程并不完全统一。在粒子跟踪中,湍流分散力通过对连续相速度附加一个随机扰动实现湍流分散,然后更新拉格朗日ODE更新粒子速度:
\begin{equation}\label{dpm}
\frac{\rd \bfU_\rd}{\rd t}=-\frac{\bfU_\rd-\left(\overline{ \mathbf{U}
_ \rc}+\mathbf{U}'\right)}{\tau_\rd}
\end{equation}在欧拉模型中,湍流分散则需要在动量方程中添加一个力源项$\mathbf{M}$来实现。通过力作用于速度实现粒子的湍流分散。
\begin{equation}\label{EE}
\frac{{\p \left( {{\alpha_\rd}{\rho_\rd}{\bfU_\rd}} \right)}}{{\p t}} + \nabla \cdot \left( {{\alpha_\rd}{\rho_\rd}\left( {{\bfU_\rd} \otimes {\bfU_\rd}} \right)} \right) - \nabla \cdot \left( {{\alpha_\rd}{\rho_\rd}{\bfR_\rd}} \right)
= ... - {\bfM_\mathrm{turb.Disp.Force}}.
\end{equation}Open Question
可见欧拉欧拉模型下的湍流分散力完全完全不同于拉格朗日下的随机行走模型。一个是通过力控制速度,如方程\eqref{EE},一个是直接在连续相速度上添加脉动,如方程\eqref{dpm}。
一些较新的算法,需要在拉格朗日框架下,融合宏观模型的湍流分散处理方法。更直白一下,能否将欧拉模型的湍流分散力直接用于拉格朗日粒子跟踪?进而抛弃传统的随机行走模型? 也就是说在拉格朗日速度ODE方程右边直接添加一个力源项来处理?
\begin{equation}
\frac{\rd \mathbf{U}}{\rd t}=\mathrm{...}+\mathrm{turb.Disp.Forces?}
\end{equation} -
-
Uc是粒子位置的气体速度
-
随机扰动实际上是附加给粒子位置的气体速度的
-
湍流分散力在泥沙的悬浮运动中非常重要。欧拉方程中湍流分散力有两种表示形式:1.如上文所言,在拖曳力里面加一分散项;2.在连续方程中考虑脉动速度,
如文献【(2011). A general two-phase turbulent flow model applied to the study of sediment transport in open channels. International Journal of Multiphase Flow, 37(9), 1099-1108.】中方程2的写法。
相关推导过程在文献【 Jha, S. K. , & Fabián A. Bombardelli. (2010). Toward two-phase flow modeling of nondilute sediment transport in open channels. Journal of Geophysical Research Earth Surface, 115(F3), -.】里面的附录里也有。 -
恩,我这边用的是MFIX,还没有植入。openfoam也有人植入过的,【A general numerical model for surface waves generated by granular material
intruding into a water bodyhttps://doi.org/10.1016/j.coastaleng.2018.09.001
里面的公式27

