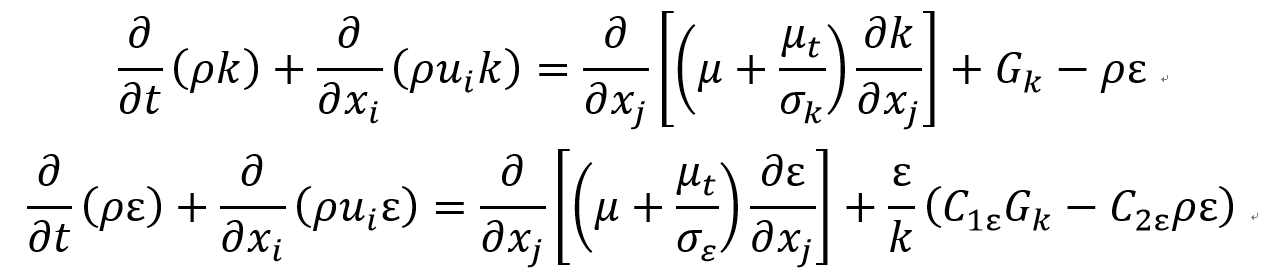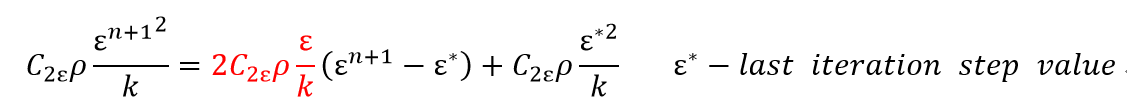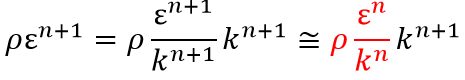OpenFOAM中标准k-e湍流模型的一点疑问
-
对于standard k-$\epsilon$ 模型,其k与$\epsilon$的控制方程如下:
\begin{equation}
\frac{\partial }{\partial t}\left ( \rho k \right )+\frac{\partial }{\partial x_{i}}\left ( \rho u_{i}k\right )=\frac{\partial }{\partial t}\left [ \left ( \mu +\frac{\mu_t}{\sigma_{k}} \right ) \frac{\partial k}{\partial x_{j}} \right ]+G_{k}-\rho \epsilon
\end{equation}
\begin{equation}
\frac{\partial }{\partial t}\left ( \rho \epsilon \right )+\frac{\partial }{\partial x_{i}}\left ( \rho u_{i} \epsilon \right )=\frac{\partial }{\partial t}\left [ \left ( \mu +\frac{\mu_{ t }}{\sigma_{ \epsilon }} \right ) \frac{\partial \epsilon }{\partial x_{j}} \right ]+C_{1\epsilon}\frac{\epsilon}{k}G_{k}- C_{2\epsilon}\rho \frac{\epsilon^2 }{k}
\end{equation}
在OpenFOAM中,其实现代码在$(FOAM_SRC)/TurbulenceModels/turbulenceModels/RAS/kEpsilon/kEpsilon.C文件中,对应的代码如下:volScalarField::Internal G ( this->GName(), nut.v()*(dev(twoSymm(tgradU().v())) && tgradU().v()) ); tgradU.clear(); // Update epsilon and G at the wall epsilon_.boundaryFieldRef().updateCoeffs(); // Dissipation equation tmp<fvScalarMatrix> epsEqn ( fvm::ddt(alpha, rho, epsilon_) + fvm::div(alphaRhoPhi, epsilon_) - fvm::laplacian(alpha*rho*DepsilonEff(), epsilon_) == C1_*alpha()*rho()*G*epsilon_()/k_() //对应epsilon方程右侧第二项 - fvm::SuSp(((2.0/3.0)*C1_ - C3_)*alpha()*rho()*divU, epsilon_) //当U不满足连续方程时的修正项? - fvm::Sp(C2_*alpha()*rho()*epsilon_()/k_(), epsilon_) //我的问题:和epsilon方程对应的右侧第三项不符 + epsilonSource() //自定义源项? + fvOptions(alpha, rho, epsilon_) //fvOption添加的源项 ); epsEqn.ref().relax(); fvOptions.constrain(epsEqn.ref()); epsEqn.ref().boundaryManipulate(epsilon_.boundaryFieldRef()); solve(epsEqn); fvOptions.correct(epsilon_); bound(epsilon_, this->epsilonMin_); // Turbulent kinetic energy equation tmp<fvScalarMatrix> kEqn ( fvm::ddt(alpha, rho, k_) + fvm::div(alphaRhoPhi, k_) - fvm::laplacian(alpha*rho*DkEff(), k_) == alpha()*rho()*G //对应k方程右侧第二项 - fvm::SuSp((2.0/3.0)*alpha()*rho()*divU, k_) //连续性误差修正项 - fvm::Sp(alpha()*rho()*epsilon_()/k_(), k_) //我的问题:与k方程右侧第三项不对应 + kSource() //自定义k源项 + fvOptions(alpha, rho, k_) //fvOption对应的源项 ); kEqn.ref().relax(); fvOptions.constrain(kEqn.ref()); solve(kEqn); fvOptions.correct(k_); bound(k_, this->kMin_);方程中,$G_{k}$为湍流生成项,一些书籍中,其定义如下,为什么代码中硬生生多出来一个$\rho$?
\begin{equation}
G_{k}=-\rho \overline{u_{i}^{'}u_{j}^{'}}\frac{\partial u_{j}}{\partial x_{i}}\simeq 2\mu_{t}s_{ij}s_{ij}
\end{equation}
我的问题写在了注释上了,是我的湍流方程写错了,还是OpenFOAM中对湍流方程有着特殊的处理?请各位老师指点