计算流体力学中的网格生成技术
-
有限体积法中网格分类方法有很多,按照节点的排列是否有序可以分为结构化网格(structured grid)和非结构化网格(unstructured grid),所谓的结构化网格就是节点排列有序,节点之间的联系信息不需要专门存储。正交曲线坐标系和适体坐标系的网格就属于结构化网格,结构化网格中还有一种是多块结构化,即结构化网格分块,比如Patched 拼片式网格和搭接式网格(overlapping)。非结构化网格是指节点排列无序,节点之间的联系信息需要专门存储。比如Delaunay三角形化网格和前沿推进法生成的网格以及单元切割法和浸没边界法(immersed Boundary Method IBM)生成的网格。按照节点运动状况可以将网格分为运动网格和静止网格。按照节点分布在计算过程中的变动情况可以分为自适应网格(self-adaptive grid)和非自适应网格。
块结构化网格为常见的结构化网格,块结构化网格的基本思想为:整个求解区域根据实际情况分成数小块,每块按常规结构化网格进行离散,各块中可采用适体坐标,以适应不规则区域的需要;各块间网格线不必连续。其具有以下优点:减轻复杂区域网格生成的难度;
便于采用并行算法;便于照顾到不同区域中不同空间尺度的需要。例如Thakur S, Shyy W,Udarkumar H S. Numer Heat Transfer, B, 1998,33;367-396 文献中采用该方法对燃气烟道进行网格划分模拟。块结构划分思路如下图所示
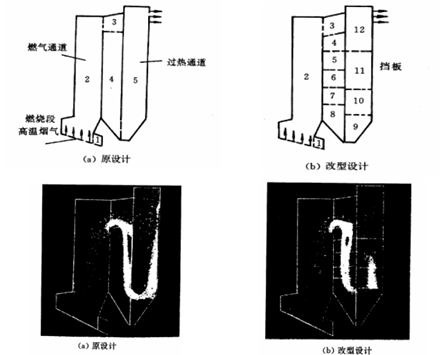
块结构化网格中有拼片式(patched)和搭接式(overlapping)。拼片式在疏密网格之间没有重叠区域。如下图所示
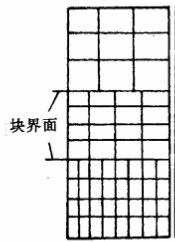
而搭接式则存在疏密网格之间的重叠区域,同时网格线一定贯穿。如下图所示

块结构化网格的主要研究问题为疏密网格交界处与疏密网格重叠区的信息传递。信息传递问题相对复杂,在此暂不分析。
非结构化网格中节点与节点间的关系没有固定的原则可循,节点与节点及节点与单元间的联系信息必须予以存储,每个单元与其周围单元的关系以及单元位置不能简单地通过递推来决定的网格系统。
非结构化网格的分类
按生成方法分:主要有Delaunay三角形法,前沿推进法等方法;按照非结构化网格的形状可以分为三角形,四边形,多边形,以及四面体六面体和多面体单元。
一般来说,生成非结构化网格之前会已知计算区域及其边界上的节点分布,需确定计算区域内的节点位置及其相互间的连接关系,在此过程中研究重点主要有三个:
- 如何向计算区域内布置节点?
- 如何连接这些节点,确定节点间联系信息?
- 如何高效地存取节点间的联系信息?
非结构化网格中节点的布置方法主要有单元顶点法和单元中心法,一般来说,单元中心法的离散过程难度较小。
非结构化网格的生成方式较为复杂,前沿推进法可以参考以下文献:
George P I, Serone E. The advancing front mesh generation method revisited. Int J Numer Methods Fluids, 1994, 37:3605-3619参考文献:陶文铨 《计算传热学的近代进展》
-
感谢分享!
