对控制方程有些疑惑,路过大神给解解惑吧!?
-
内能形式和总能形式
这个根据OpenFOAM基金会的文章有解释
OpenFOAM官方表示,能量方程的选择在某些情况下是至关紧要的33。比如在进行震波捕获计算的时候,求解总能量方程要比求解内能方程结果精确的多。
http://www.dyfluid.com/energy.html
http://cfd.direct/openfoam/energy-equation -
前面的回答有错误,我给你一个总结版的:
首先,明确守恒形式和非守恒形式数学上完全等价。
守恒和非守恒的区别:
守恒形式—在空间固定的控制体(控制体位置、形状不变)上推导而来,所有流程变量全部写在偏导符号内(这里又分为强守恒和弱守恒,这不重要不用管)。
非守恒形式—在运动的控制体上(永远由相同的流体微团构成)推导而来,有的流场变量在偏导外。使用守恒型的原因有两个(仅讨论积分形式下的,微分形式无法处理间断):
- 程序和算法设计方便,守恒形式可以写成统一的格式。
- 数值计算上能减少误差,守恒型方程在流场有间断时(比如接触间断、激波之类),能得到平滑的解而非守恒型则容易产生震荡。这一点最早的时候只是激波捕捉计算时得到的经验,不过理论上也站得住脚,守恒型方程的守恒变量在跨过激波时要么很小要么为零,所以能提高激波数值解的质量。
所以说,如果流场有间断,采用积分形式的守恒方程为佳。
至于内能和总能的形式,从@cfd-china 给出的OpenFOAM官方资料看,它们计算了典型的激波管问题(一维Euler方程的Riemann问题),采用总能的形式,守恒变量在跨过激波时保持不变,而内能形式则不能保证。归根结底,还是因为间断的场比连续的场更难模拟。
-
我也补充几点,从数学上:
- 守恒形式和非守恒形式都具有积分形式和微分形式;
- 积分形式方程是从有限体积(体积为V)得来。微分形式是从无穷小有限流体微元(体积为dV)得来;
- 更进一步,从位置固定有限体积(体积为V)得来的是积分形式下的守恒形式方程;
- 从随流线流动有限体积(体积为V)得来的是微分形式下的守恒形式方程;
- 积分形式方程求解有限体积V上的量的平均比较简单,比如求解有限体积面上的压力,微分形式方程求解无穷小有限流体微元,可以获得量的局部分布。
- 积分形式确实不需要连续,微分形式需要连续;
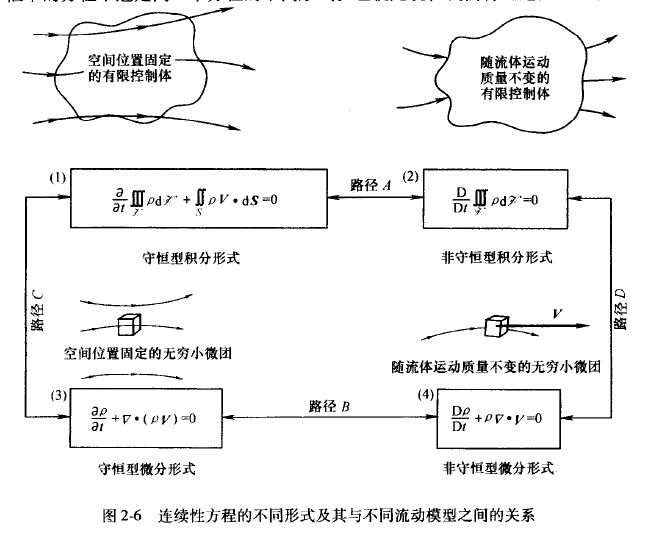
守恒方程和非守恒方程在安德森的书中被讨论的极为、非常、完全的充分。建议仔细再仔细的参考这本书。
More general:
- 守恒形式非守恒形式可以完全转化;
- 如果FVM和强守恒形式一起使用。自动就利用了守恒这个特性。FDM则需要强加某些条件。FVM中,整个计算域其实就是一个一个有限体积;
- 非守恒形式离散后可能会产生一个源项。例如,在对连续性方程离散的时候,离散后从边界的通量和应该是0。但是采用非守恒形式会在方程右边产生一个源项。对于连续流这个源项非常小,但是对于不连续流动(超音速流),这个源项会产生比较大的误差;
