Re: icoFoam解析中的问题
-
原帖地址:https://cfd-china.com/topic/3804/icofoam解析中的问题/6
26式从里往外:$p^{t+\Delta t}$(标量)
-
$p^{t+\Delta t}_f$(表面力在面上的梯度,矢量,在面法向的投影)
-
$\sum p^{t+\Delta t}_f \mathbf{S}_f$(矢量的面积分,
散度,标量) -
$(\frac{1}{V_p}\sum p^{t+\Delta t}_f \mathbf{S}_f)_f$(标量在面上的
梯度,矢量) -
$\sum\frac{1}{A_{P,f}}(\frac{1}{V_p}\sum p^{t+\Delta t}_f \mathbf{S}_f)_f\cdot\mathbf{S}_f$(矢量的面积分,散度,标量)
你刚开始问的先求散度再求梯度指的是2、3。
为什么把加下标 $_f$ 称为梯度操作,这里虽然没有矢量,却人为规定了p是面上力垂直于面的分量(正应力),面上力平行于面的分量放到切应力里了。所以 $p_f$ 就是压力的梯度在面法向上的投影,它乘以面矢量 $\mathbf{S}_f$ 再求和就是计算散度。(这里准确来说不是梯度。如果对一个标量场求偏导数,通常称最大偏导数为梯度,最大偏导数的增长方向为梯度方向。这个可以说是梯度在面法向上的投影。即(7)式上面一行提到的“面法向梯度”。)
如果要理解最好给这个通过面积分计算散度的过程取个名字,比如叫“封闭面积分”
,因为“散度”更像是一个物理量而不是一个操作过程。散度就像质量、转动惯量一样是个客观属性,封闭面积分 是计算散度的一种方法,另一种方法是直接对散度进行体积分。两种方法结果相等叫高斯定理。散度的值就是封闭体内“源”的“数量”。如果换成电比较好理解。散度就是封闭体内有几个电荷。梯度就是两点间电荷量差值(电压)($电压=\frac{电荷量}{电容}$),当然是个方向中差值最大的那个。
这样,梯度是用电荷量(标量)求电场(有向电压),散度是通过电场(有向电压)对面积分求封闭体内电荷(相对的)。这两个操作是互逆的,区别点在,经过梯度、散度后得到的结果是“相对的”,因为求梯度这个操作把绝对值磨平了。『比如原来电荷(电压)分布是"0|1 5 7|0",面上梯度(即偏导数)(电场矢量)是"1 4 2 7",散度是-1+7=“6”』,散度积分积的也是这个磨平的量。
除以体积2,平均散度是“3”。平均后电场是"0|(x) (x+3) (x+3+3)|0"。
散度是“作用量”,相对的,1.2.是把相对的值提了出来。3.4.是把“作用量”平均了再接着先梯度再散度。至于为啥平均,一步步推过来,慢慢往回找……我找到(14)->(19)式断了,(14)式可以写为(19)式,(19)式突然就多了个$\frac{1}{V_p}$。
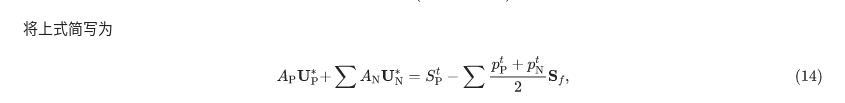

$p_f^{t}=\frac{p_P^t+p_N^t}{2}$是(11)式没问题。如果只理解这两个式子就是:$\nabla p^{t+\Delta t}$(连续的)$=(\frac{1}{V_p}\sum p^{t+\Delta t}_f \mathbf{S}_f)_f$(离散的)
梯度散度再梯度,饶了一圈,不过把散度对体积平均了。非要解释就是连续的梯度是指处处的梯度、而离散的梯度不是,平均之后是,是等效的。
上面是我猜的,下面是保证靠谱的。
标量不可以求散度,结合上面说的,散度是封闭体内的物理属性,除了对散度进行体积分求散度外,常用 封闭面积分 计算。封闭面积分只能用面上适量与面向量乘积求和,才得到标量的散度值(电荷量)。用面上标量乘面向量再求和不还是向量,不是散度值,也没有物理意义。
出发点是求某物理量的净增量,散度,但是直接对散度进行体积分不方便,无法探测这个体内无穷多个点的散度值,但是可以探测这个体表面的有向流量判断体内有没有源(散度值)
方程用散度等来等去就是求源头,因为物理守恒定律就是源为零,除非加人为扰动,这也是为啥最后一项叫源项。
-
-
麻烦东岳老师了,谢谢!
-
按照@bestucan 老师的解释,我大概就能理解了,之前我一直把$p_{f}$当做一个标量来看待,所以有些不理解
-
@warnerchang 我不是老师,我只是个研究生

我是这样理解的,也没找谁验证过,不一定对,兴许以后你能找到更靠谱的解释。




 写出来一是分享,二来有错的,大家能指出来,老师不用太在意,兴许是逻辑相当自恰的错误连篇
写出来一是分享,二来有错的,大家能指出来,老师不用太在意,兴许是逻辑相当自恰的错误连篇