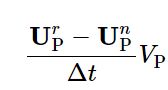关于 phi 和 fvVectorMatrix 的两个问题
-
东岳老师,非常感谢您的回复!
对于第一问题,我又进行了尝试,下面是我的理解,如果有不对的地方,还请您指正。
边界上的phi可以由边界条件得到,在cavity这个算例中,边界上没有法向的速度,因而phi全部为‘0’。而在internal face上的phi,可以由已知的速度场进行差值得到face上的速度,再乘以该face的面积和法向,就得到了phi。对于第二个问题,我又输出了U的值。
Info<< " U " << U << nl << endl;得到
U dimensions [0 1 -1 0 0 0 0]; internalField nonuniform List<vector> 16 ( (-0.00109257 0.00108567 0) (-0.00260853 0.000420926 0) (-0.00260827 -0.000416558 0) (-0.0010966 -0.00108186 0) (-0.00181643 0.00400068 0) (-0.00421015 0.00141225 0) (-0.00421276 -0.00140849 0) (-0.00182014 -0.00400052 0) (-0.0033937 0.00937929 0) (-0.00774594 0.0025887 0) (-0.00774527 -0.00258687 0) (-0.00339316 -0.00937899 0) (0.0210076 0.00646146 0) (0.0145416 0.00159495 0) (0.0145415 -0.00159377 0) (0.0210087 -0.00646063 0) ) ; boundaryField { movingWall { type fixedValue; value uniform (1 0 0); } fixedWalls { type noSlip; } frontAndBack { type empty; } }发现 UEqn_time_term.source() 里面的值对应为速度的值除以时间步长再乘以对应cell的体积。(时间步长为0.001,体积为0.01乘以0.025乘以0.025)
-
东岳老师,我在研究完icoFoam中的 ‘fvm::ddt(U)’ 和 ‘fvm::div(phi, U)’ 之后又进而研究了‘fvm::laplacian(nu, U)’,有如下几个问题没有弄明白。
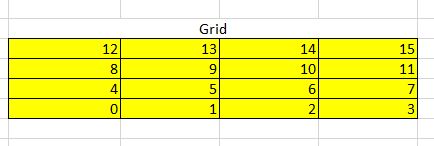
为了看的清楚,附上网格编号的图。
我分别定义了不同的 fvVectorMatrix
fvVectorMatrix UEqn_time_term ( fvm::ddt(U) ); fvVectorMatrix UEqn_advection_term ( fvm::div(phi, U) ); fvVectorMatrix UEqn_diffusion ( fvm::laplacian(nu, U) );对他们进行输出之后发现 UEqn_time_term 和 UEqn_advection_term 的diag() 和A() 每个元素都是相差一个cell 的体积
UEqn.A() = UEqn.diag()/mesh.V()但是UEqn_diffusion的diag() 和A()只有在非边界的单元才满足上述关系。如下
UEqn_diffusion.diag 16 ( -0.0002 -0.0003 -0.0003 -0.0002 -0.0003 -0.0004 \\这个满足上面的关系 -0.0004 \\这个满足上面的关系 -0.0003 -0.0003 -0.0004 \\这个满足上面的关系 -0.0004 \\这个满足上面的关系 -0.0003 -0.0002 -0.0003 -0.0003 -0.0002 ) UEqn_diffusion.A dimensions [0 0 -1 0 0 0 0]; internalField nonuniform List<scalar> 16 ( -96 -80 -80 -96 -80 -64 -64 -80 -80 -64 -64 -80 -96 -80 -80 -96 ) ; boundaryField { movingWall { type extrapolatedCalculated; value nonuniform List<scalar> 4(-96 -80 -80 -96); } fixedWalls { type extrapolatedCalculated; value nonuniform List<scalar> 12 ( -96 -80 -80 -96 -96 -80 -80 -96 -96 -80 -80 -96 ) ; } frontAndBack { type empty; } }我的第一个问题是 在UEqn_diffusion中.A()是怎么计算的?
我在输出UEqn_diffusion的时候也发现它与其他的输出结果不同,在网上搜了半天也没有得到答案。
Info<< " UEqn_diffusion " << UEqn_diffusion << nl << endl;输出结果如下:
UEqn_diffusion false true true 16 \\这个应该是diag() ( -0.0002 -0.0003 -0.0003 -0.0002 -0.0003 -0.0004 -0.0004 -0.0003 -0.0003 -0.0004 -0.0004 -0.0003 -0.0002 -0.0003 -0.0003 -0.0002 ) 24 \\这个应该是upper ( 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 ) [0 4 -2 0 0 0 0] 16{(0 0 0)} \\我猜这个是source,这里面没有源项,4by4的网格,应该都是零。如果不对,请您指正。 3 \\从这个开始往下我不知道是什么了,其他的matrix这些项都是零,请问这些值都代表了什么? ( 4((-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002)) 12 ( (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) (-0.0002 -0.0002 -0.0002) ) 0() ) 3 ( 4((-0.0002 -0 -0) (-0.0002 -0 -0) (-0.0002 -0 -0) (-0.0002 -0 -0)) 12{(-0 -0 -0)} 0() )第二个问题 写在了代码的注释里,主要是不明白这个输出的结果里面除了diag(), upper() 和source()之外的那些项是什么?
我在推倒UEqn_diffusion 的系数矩阵的时候发现,由边界条件得到边界上的速度值,那么最上面的滑动边界上的cell (编号为P)
\begin{equation}
S_{e}\nu_{e}\frac{u_{E}-u_{P}}{\Delta x} + S_{w}\nu_{w}\frac{u_{W}-u_{P}}{\Delta x} + S_{n}\nu_{n}\frac{u_{N}-u_{P}}{\Delta y} + S_{s}\nu_{s}\frac{u_{S}-u_{P}}{\Delta y}
\end{equation}里面的$u_{N}$可以根据边界条件差值
\begin{equation}
u_{N} = 2 u_{n} - u_{P}
\end{equation}其中$u_{n}$为上面滑动边界已知的速度。
但是这个边界条件并没有在系数矩阵的diag()中体现出来,这也带来了我的第三个问题,这个边界条件在 UEqn_diffusion 是怎么体现出来的?是否与第二个问题有关?
第四个问题就是也是又第三个问题引出来的,我试着求解了一下UEqn_diffusion,并输出了一下U的结果
solve(UEqn_diffusion); Info<< " U solution " << U << nl << endl;但这次与前面的 UEqn_time_term 和 UEqn_advection_term 不同, 没能找到其结果和UEqn.A() 与UEqn.H() 的关系。
我的问题有点儿多,我也会继续查找相关的信息,期待您的解答!
非常感谢!
-
@cfd-china 谢谢您!我是刚开始学Openfoam,希望能多多向前辈们请教!
-
补充一下上面的帖子
solve(UEqn_diffusion); Info<< " U solution " << U << nl << endl;结果如下:
smoothSolver: Solving for Ux, Initial residual = 0.921181, Final residual = 9.32208e-06, No Iterations 11 smoothSolver: Solving for Uy, Initial residual = 0.999778, Final residual = 8.66271e-06, No Iterations 8 U solution dimensions [0 1 -1 0 0 0 0]; internalField nonuniform List<vector> 16 ( (0.0189067 -1.2469e-08 0) (0.0430646 -3.74215e-08 0) (0.0430639 -4.90001e-08 0) (0.0189057 -2.83642e-08 0) (0.0703756 -3.73926e-08 0) (0.153354 -1.08185e-07 0) (0.153353 -1.33266e-07 0) (0.070374 -6.9139e-08 0) (0.179619 -4.88555e-08 0) (0.34663 -1.32978e-07 0) (0.34663 -1.48122e-07 0) (0.179618 -6.64227e-08 0) (0.481091 -2.81724e-08 0) (0.706929 -6.88449e-08 0) (0.706929 -6.63391e-08 0) (0.481091 -2.54916e-08 0) ) ; boundaryField { movingWall { type fixedValue; value uniform (1 0 0); } fixedWalls { type noSlip; } frontAndBack { type empty; } }但这次与前面的 UEqn_time_term 和 UEqn_advection_term 不同, 没能找到其结果和UEqn.A() 与UEqn.H() 的关系。感觉openfoam求解了这个方程,从UEqn_diffusion的系数和source()项为零来看,求解结果应该是零,但是显然是我想错了。如果是$u_{P}$为未知,$u_{W}$等相邻的cell的速度用的是上一个时间步的值,那么线性方程组只存在对角线的值,不需要迭代,直接就能出结果。在这个问题上没有想明白,还希望您能指点一下这个方程是怎么求解的。
-
@wwzhao
即使没有在方程等号右边添加源项的fvMatrix,比如:fvScalarMatrix TEqn ( fvm::ddt(T) );这个矩阵系统依然具有源项。显性离散的值全部进入了
fvMatrix的source()。P.S. 这个问题@mengweilm425 不是在一楼测试过了么?
用一个网格单元测试:#include "fvCFD.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { #include "setRootCase.H" #include "createTime.H" #include "createMesh.H" volScalarField T ( IOobject ( "T", runTime.timeName(), mesh, IOobject::NO_READ, IOobject::NO_WRITE ), mesh, 1 ); fvScalarMatrix TEqn ( fvm::ddt(T) ); Info<< "source" << TEqn.source() << endl; } -
针对@mengweilm425 提到的
A()和diag()。区别是A()=diag()/V;可测试:#include "fvCFD.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { #include "setRootCase.H" #include "createTime.H" #include "createMesh.H" volScalarField T ( IOobject ( "T", runTime.timeName(), mesh, IOobject::NO_READ, IOobject::NO_WRITE ), mesh, 1 ); fvScalarMatrix TEqn ( fvm::ddt(T) ); Info<< "source" << TEqn.source() << endl; Info<< "source" << TEqn.A() << endl; Info<< "source" << TEqn.diag() << endl;//diag() equals TEqn.A() multiply mesh.V() }源代码:
template<class Type> Foam::tmp<Foam::volScalarField> Foam::fvMatrix<Type>::A() const { tmp<volScalarField> tAphi ( new volScalarField ( IOobject ( "A("+psi_.name()+')', psi_.instance(), psi_.mesh(), IOobject::NO_READ, IOobject::NO_WRITE ), psi_.mesh(), dimensions_/psi_.dimensions()/dimVol, extrapolatedCalculatedFvPatchScalarField::typeName ) ); tAphi.ref().primitiveFieldRef() = D()/psi_.mesh().V(); tAphi.ref().correctBoundaryConditions(); return tAphi; }template<class Type> Foam::tmp<Foam::scalarField> Foam::fvMatrix<Type>::D() const { tmp<scalarField> tdiag(new scalarField(diag())); addCmptAvBoundaryDiag(tdiag.ref()); return tdiag; } -
@cfd-china 离散的具体实现可参阅相关源码。
以
fvm::ddt(T)为例,调用的是template<class Type> tmp<fvMatrix<Type> > ddt ( const GeometricField<Type, fvPatchField, volMesh>& vf ) { return fv::ddtScheme<Type>::New ( vf.mesh(), vf.mesh().ddtScheme("ddt(" + vf.name() + ')') )().fvmDdt(vf); }这里调用了
fv::ddtScheme<Type>::New,这个函数是一个runtime construction的实现,即在运行时读取字典文件中的离散格式并构造相应的对象:template<class Type> tmp<ddtScheme<Type> > ddtScheme<Type>::New ( const fvMesh& mesh, Istream& schemeData ) { if (fv::debug) { Info<< "ddtScheme<Type>::New(const fvMesh&, Istream&) : " "constructing ddtScheme<Type>" << endl; } if (schemeData.eof()) { FatalIOErrorIn ( "ddtScheme<Type>::New(const fvMesh&, Istream&)", schemeData ) << "Ddt scheme not specified" << endl << endl << "Valid ddt schemes are :" << endl << IstreamConstructorTablePtr_->sortedToc() << exit(FatalIOError); } const word schemeName(schemeData); typename IstreamConstructorTable::iterator cstrIter = IstreamConstructorTablePtr_->find(schemeName); if (cstrIter == IstreamConstructorTablePtr_->end()) { FatalIOErrorIn ( "ddtScheme<Type>::New(const fvMesh&, Istream&)", schemeData ) << "Unknown ddt scheme " << schemeName << nl << nl << "Valid ddt schemes are :" << endl << IstreamConstructorTablePtr_->sortedToc() << exit(FatalIOError); } return cstrIter()(mesh, schemeData); }以常见的
Euler格式为例,将会构造EulerDdtScheme类型的对象,并用其fvmDdt()方法返回的fvMatrix,看fvmDdt()的实现:template<class Type> tmp<fvMatrix<Type> > EulerDdtScheme<Type>::fvmDdt ( const GeometricField<Type, fvPatchField, volMesh>& vf ) { tmp<fvMatrix<Type> > tfvm ( new fvMatrix<Type> ( vf, vf.dimensions()*dimVol/dimTime ) ); fvMatrix<Type>& fvm = tfvm(); scalar rDeltaT = 1.0/mesh().time().deltaTValue(); fvm.diag() = rDeltaT*mesh().Vsc(); if (mesh().moving()) { fvm.source() = rDeltaT*vf.oldTime().internalField()*mesh().Vsc0(); } else { fvm.source() = rDeltaT*vf.oldTime().internalField()*mesh().Vsc(); } return tfvm; }可以看到
fvm::ddt(T)产生的fvm.diag()为时间倒数乘以网格单元体积,其产生的源项fvm.source()为时间倒数乘以上一时刻的T乘以网格单元体积。对于fvm::div及fvm::laplacian可以做类似分析。
插一句,fvm::div离散不会产生source(),fvm::laplacian会产生source()。
-
非常感谢大家的回复!我现在的阶段还看不好代码,但是我又对fvMatrix做了一些测试。
还是如下的fvMatrix
fvVectorMatrix UEqn_diffusion ( fvm::laplacian(nu, U) );我发现在解这个方程的时候
\begin{equation}
[A][x]=[b]
\end{equation}矩阵[A] 实际上是 UEqn.D() + UEqn.upper() + UEqn.lower(), 而没有使用UEqn.diag()。UEqn.D()在UEqn.diag()的基础上加上了边界条件对当前网格的影响。上面方程中的[b],也不是UEqn.source(),而是和边界条件中已知的速度相关的值。我直接求解得到的结果和openfoam算出来的结果是一样的。由于没有真正的去看代码,不知道Openfoam里面有没有相关的function可以直接输出上述$[A][x]=[b]$方程组中的[A]和[b],还请各位大神指点。
再次感谢大家的帮助!
-
@mengweilm425 $[A][x]=[b]$ 中的 [A] 可以看成是 internal field 离散后的系数矩阵和 boundary conditions 对系数矩阵的影响两部分之和,其中 internal field 离散之后的系数矩阵表示为 upper(),diag() 和 lower()。boundary condition 对系数矩阵的影响则放在 internalCoeffs_ 里面。[b] 也一样,可以分为 internal field 产生的源项 source(),及 boundary conditions 对源项的影响 boundaryCoeffs_。
OpenFOAM中没有直接输出 [A] 和 [b] 的函数,关于如何将 boundary conditions 的影响加到 fvMatrix 里面,你可以参考 addBoundaryDiag,addCmptAvBoundaryDiag 及 addBoundarySource 这几个函数。
@wwzhao 在 关于 phi 和 fvVectorMatrix 的两个问题 中说:
@李东岳 fvMatrix的source并不是线性代数方程组Ax=b中的b,而是指加在网格单元中心的力源项。
上面的帖子描述不太准确,确切说 [b] 是 internal field 产生的源项 source() + boundary field 产生的源项 boundaryCoeffs_。
-
@mengweilm425 您好 看了你的研究过程,觉得很好。我也想这样分步骤运行各个程序,以分清各个量含义。请问您是怎么做到的。我先编译了自己求解器,在文件中加入自己想输出的量,希望在输出中出现想看到的量。结果并没有看到想看的内容。请问您是如何。。