《无痛苦N-S方程笔记》勘误

wangfei9088

最近几天再看这半部书，感觉收获很多，不只是加深印象，对很多问题也有了新的认识。基于2020年12月29日修订版，也就是东岳流体今天下载的那个版本有一些typo。说得不对的地方，还请东岳老师包涵。

第一页倒数第二行：
初学者也不看的不明不白。
是不是多了个“不”？

第二页第一行和第二行：
GCFD 课程因此分为两步，第一步是基本的N-S 方程入门，第二部是N-S 方程求解。第一步需要同学们通过本笔记进行预习。第二部将在GCFD 课程上讲授。
“部”应该是“步”？

第三十四页4.1.4节第二行：
另但是大量的文献依旧通过二维大涡模拟、甚至二维直接模拟进行相关研究。例如，Bouris and Bergeles 的文章中表示[7]
多了个“另”？

第三十五页第二段引用：
我们的研究表示二维的大涡模拟，甚至直接模拟完全是扯淡的。
研究表明？

第三十五页4.2节第一段倒数第二行：
定于网格节点与面相连接的序号等。
这个是“定义”？

第三十六页4.2.1节第二段第二行和第四行：
左侧速度的方向与面试量为近似同向，因此Sf · Uf 为正值。同时，owner 单元的流体流出，neighbour 单元有流体流入。右侧度的方向与面试量为近似反向，因此Sf · Uf 为负值。
两个应该都是“面矢量”？

第三十九页倒数第十一行：
在这种情况下，方程(4.29)变为：
这里应该是“方程(4.24)”？

第四十六页：

方程4.69应该是最后一个“dβ”应该是“dγ”？
然后对其求解散度项中代入到动量方程中进行显性离散计算。
这个“中”是不是要换成“再”？

2021年第一个回帖，祝各位老师新的一年计算收敛，多发paper！新年快乐！！！

李东岳

@wangfei9088 非常感谢！已更新。最新版本的方程4.29、以及四十六页的没太对上，你看新版本的是哪个不？

wangfei9088

@李东岳啊，东岳老师，刚重新对了一下东岳流体上的文档。不好意思，是我写错了。应该是这样的：

第四十一页：
方程4.43多了“Am”？

第四十一页倒数第八行：
在这种情况下，方程4.47变为：
这里应该是“方程(4.42)”？

第四十六页：
方程4.79最后一个“dβ”应该是“dγ”？

第四十七页第二段最后一行：
然后对其求解散度项中代入到动量方程中进行显性离散计算。
这个“中”是不是要换成“再”？

我写的勘误不一定都对，请东岳老师斟酌。

李东岳

@wangfei9088 非常感谢！全部都更正了！

顺便又更新了一下

麦克斯韦分布与高斯分布
矩方程、五矩模型、十矩模型以及欧拉方程

wangfei9088

@李东岳作为伸手党，应该是我们感谢您！
其实这两个人都是我
捕获.PNG

CUGB_Zhou

受教了，谢谢

Kingkong

最近重看笔记，刚看了前言发现两个小笔误。
（1）前言第二段：Computational译为“计算”。Fluid Dynamics则为流体动力学。计算后的句号是否应为逗号？
（2）IV页“总而言之”这段第5行“玩弄于掌股”是否为“玩弄于股掌”？
两处无关紧要的笔误(*￣︶￣)

李东岳

@kingkong 谢谢，已更新，你看下

wangfei9088

@李东岳
第95页（页码是83页）公式（7.27）中的
$$
\frac{\alpha}{m_0} ^ {2/3}
$$
加个括号应该会更好吧。
$$
(\frac{\alpha}{m_0}) ^ {2/3}
$$

wangfei9088

更新一个笔误。图中的$y^{*}$应该是
$$y^*=\frac{\sqrt{k} y}{\nu}$$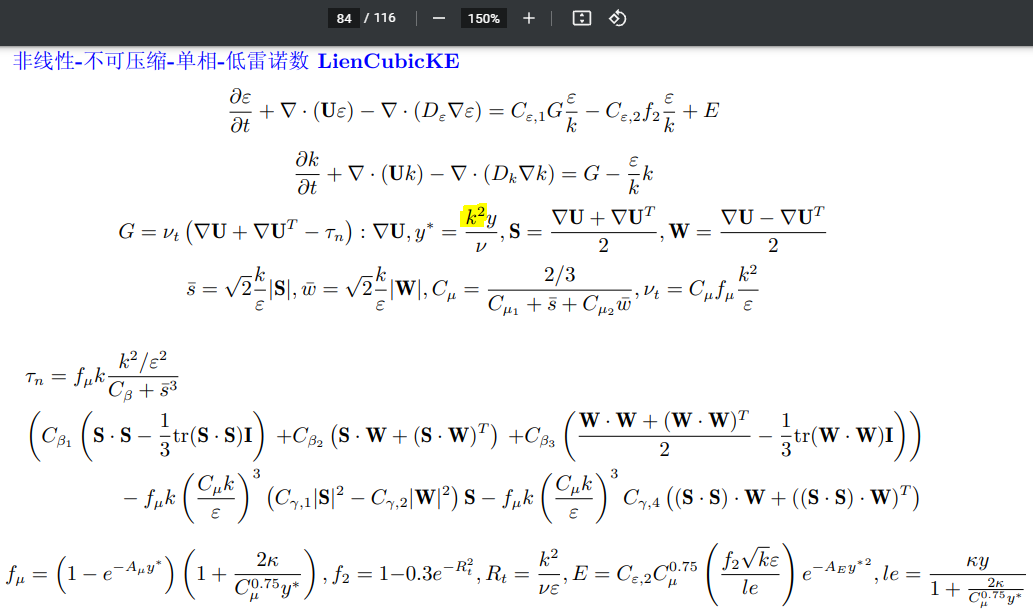

李东岳

谢谢！已更新

wangfei9088

图中的$r$应该是
\begin{equation}
r=\min\left(\frac{\nu+\nu_t}{|\nabla \mathbf{U}| \kappa^2 \tilde{d}^2}, 10\right)
\end{equation}
后面$\tilde{d}$更严格的写法应该是
\begin{equation}
\tilde{d}=\max\left[y-\left(1- \tanh\left(\left(8r\right)^3\right)\right) \max\left(y-C_{DES}\Delta, 0\right), 0\right]
\end{equation}

请东岳老师斟酌。

李东岳

@wangfei9088 多谢大佬检查。稍后更新。大佬把湍流模型捋了个遍么。做什么研究方向的

wangfei9088

@李东岳哈哈，东岳老师，我不是大佬。小青铜科研找不到方向和突破口，只能多看看书。确实这次基本把湍流模型都撸了一遍，模型加代码。每次看这本笔记都收获很大。

李东岳

@wangfei9088 厉害厉害，最近我把壁面函数更新一下

wangfei9088

@李东岳学无止境，接着嗨

袁宝强

LienLeschziner低雷诺数湍流模型勘误。

Openfoam *.c文件中源码和出处

tmp<volScalarField> LienLeschziner::fMu() const
{
    const volScalarField yStar(sqrt(k_)*y_/nu());

    return
        (scalar(1) - exp(-Anu_*yStar))
       /((scalar(1) + SMALL) - exp(-Aeps_*yStar));
}

以下是原论文出处
Lien, F., and Leschziner, M. A. (December 1, 1993). "A Pressure-Velocity Solution Strategy for Compressible Flow and Its Application to Shock/Boundary-Layer Interaction Using Second-Moment Turbulence Closure." ASME. J. Fluids Eng. December 1993; 115(4): 717–725.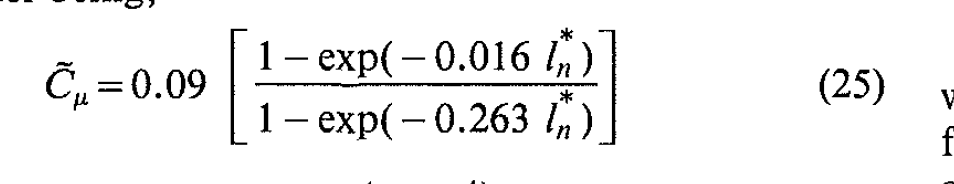

李东岳

@袁宝强已更新，多谢老铁

ESAYUAN

@李东岳东岳老师我在学习过程中跟着公式推导发现3.4.4条中的最后一步应该是将方程（3.51）带入到方程（3.50），是笔误吧？

Tong

hello李老师~ 最近看了看这本笔记，发现有的地方有点小问题~~~。
（1）多孔介质部分，P115页，公式7.58的以及后文的注解中，您将D解释为渗透率(permeability or k)，这应该是有些不准确的，根据达西公式描述的压力速度关系，渗透率的量纲为m^2 (https://www.calculator.org/properties/permeability.html)，通常左乘压力梯度(可以参考[1]中达西公式描述(Equation-(1)))，OF中的多孔介质模型实现是在动量方程添加阻力源项来实现的，与达西公式不同的是：在公式7.59中，D左乘了速度(U)，大小为渗透率的倒数，量纲为m^-2，为了避免误解，在这里解释D为达西阻力系数，F为 Forchheimer 阻力系数更合适，多孔介质渗透率(k)越大对应的达西阻力系数（D）就越小，反之亦然。个人观点：将” 沉降项 “翻译成”阻力源项“更好理解，也和Fluent的手册里对这种实现方法的解释一致。
(2)同时在 P125页中 7.9.6 setReference()，对公式7.101的解释中，‘p无解’。实际上该方程的秩（rank）为 2（矩阵的第1、2行与第3行 线性相关），而未知数的个数为3，这种情况下，p有无穷多个线性相关解，这种情况下设置参考值能够将这无穷多个线性相关解退化到该参考值下的定解。同时，建议将rank翻译成’秩‘，符合国内线代教材对矩阵所在的线性空间的维数这一定义，用‘阶’的话容易和‘m*n阶’矩阵这种叫法中的‘阶’混淆造成误解。

[1]T. Wang and J. Yao, An improved embedded discrete fracture model and domain connectivity algorithms on 3D
unstructured grids, Journal of Computational Physics, 111142, doi: https://doi.org/10.1016/j.jcp.2022.111142. (求引用QAQ)

CFD中文网

《无痛苦N-S方程笔记》勘误