《无痛苦N-S方程笔记》勘误

[lin_lia]

[bestucan]

@bestucan 在 《无痛苦N-S方程笔记》勘误 中说：

《多相流及群体平衡模型的数值计算方法》看完了，就又发现了一个错误，不值当再开新帖了。
第十一页 倒数第一段 第二行 两处“动理学方程”->“动力学方程”

这个不是错误。是我孤陋寡闻了

[.J.]

@bestucan 学习了，我们做颗粒动理学，只知道老师这么叫我们也跟着这么叫，原来还有这样一段故事。

[Frank0514]

李老师：今天学习您的《无痛苦N-S方程笔记》发现有点小笔误：
第10页公式（2.20）下面一句话：“现在看图4中的无穷小微团”，应该是图2.5吧；
第16页、17页、18页中有几个地方写的是“收到xxx力”，应该是“受到”才对。

[李东岳]

@Frank0514 已更新，谢谢！！

[FluidGao]

方程（1.4），是不是漏了一个转置符号？

[FluidGao]

@FluidGao 在 《无痛苦N-S方程笔记》勘误 中说：

方程（1.4），是不是漏了一个转置符号？

最新版的笔记已经更新

[李东岳]

@FluidGao 啊？我才看见

[wangfei9088]

最近几天再看这半部书，感觉收获很多，不只是加深印象，对很多问题也有了新的认识。基于2020年12月29日修订版，也就是东岳流体今天下载的那个版本有一些typo。说得不对的地方，还请东岳老师包涵。

第一页倒数第二行：
初学者也不看的不明不白。
是不是多了个“不”？

第二页第一行和第二行：
GCFD 课程因此分为两步，第一步是基本的N-S 方程入门，第二部是N-S 方程求解。第一步需要同学们通过本笔记进行预习。第二部将在GCFD 课程上讲授。
“部”应该是“步”？

第三十四页4.1.4节第二行：
另但是大量的文献依旧通过二维大涡模拟、甚至二维直接模拟进行相关研究。例如，Bouris and Bergeles 的文章中表示[7]
多了个“另”？

第三十五页第二段引用：
我们的研究表示二维的大涡模拟，甚至直接模拟完全是扯淡的。
研究表明？

第三十五页4.2节第一段倒数第二行：
定于网格节点与面相连接的序号等。
这个是“定义”？

第三十六页4.2.1节第二段第二行和第四行：
左侧速度的方向与面试量为近似同向，因此Sf · Uf 为正值。同时，owner 单元的流体流出，neighbour 单元有流体流入。右侧度的方向与面试量为近似反向，因此Sf · Uf 为负值。
两个应该都是“面矢量”？

第三十九页倒数第十一行：
在这种情况下，方程(4.29)变为：
这里应该是“方程(4.24)”？

第四十六页：

1. 方程4.69应该是最后一个“dβ”应该是“dγ”？

2. 然后对其求解散度项中代入到动量方程中进行显性离散计算。
   这个“中”是不是要换成“再”？

2021年第一个回帖，祝各位老师新的一年计算收敛，多发paper！新年快乐！！！

[李东岳]

@wangfei9088 非常感谢！已更新。最新版本的方程4.29、以及四十六页的没太对上，你看新版本的是哪个不？

[wangfei9088]

@李东岳 啊，东岳老师，刚重新对了一下东岳流体上的文档。不好意思，是我写错了。应该是这样的：

第四十一页：
方程4.43多了“Am”？

第四十一页倒数第八行：
在这种情况下，方程4.47变为：
这里应该是“方程(4.42)”？

第四十六页：
方程4.79最后一个“dβ”应该是“dγ”？

第四十七页第二段最后一行：
然后对其求解散度项中代入到动量方程中进行显性离散计算。
这个“中”是不是要换成“再”？

我写的勘误不一定都对，请东岳老师斟酌。

[李东岳]

@wangfei9088 非常感谢！全部都更正了！

顺便又更新了一下

• 麦克斯韦分布与高斯分布

• 矩方程、五矩模型、十矩模型以及欧拉方程

[wangfei9088]

@李东岳 作为伸手党，应该是我们感谢您！
其实这两个人都是我

[CUGB_Zhou]

受教了，谢谢

[Kingkong]

最近重看笔记，刚看了前言发现两个小笔误。
（1）前言第二段：Computational译为“计算”。Fluid Dynamics则为流体动力学。 计算后的句号是否应为逗号？
（2）IV页“总而言之”这段第5行“玩弄于掌股”是否为“玩弄于股掌”？
两处无关紧要的笔误(*￣︶￣)

[李东岳]

@kingkong 谢谢，已更新，你看下

[wangfei9088]

@李东岳
第95页（页码是83页）公式（7.27）中的
$$
\frac{\alpha}{m_0} ^ {2/3}
$$
加个括号应该会更好吧。
$$
(\frac{\alpha}{m_0}) ^ {2/3}
$$

[wangfei9088]

更新一个笔误。图中的$y^{*}$应该是
$$y^*=\frac{\sqrt{k} y}{\nu}$$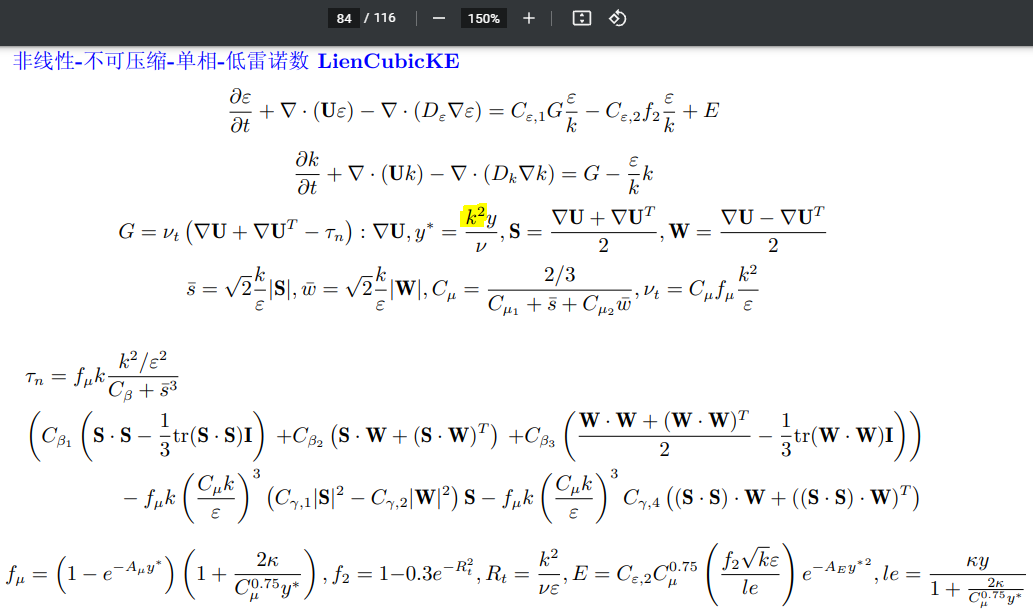

[李东岳]

谢谢！已更新

[wangfei9088]

图中的$r$应该是
\begin{equation}
r=\min\left(\frac{\nu+\nu_t}{|\nabla \mathbf{U}| \kappa^2 \tilde{d}^2}, 10\right)
\end{equation}
后面$\tilde{d}$更严格的写法应该是
\begin{equation}
\tilde{d}=\max\left[y-\left(1- \tanh\left(\left(8r\right)^3\right)\right) \max\left(y-C_{DES}\Delta, 0\right), 0\right]
\end{equation}

请东岳老师斟酌。