MPPICInterFoam 中如何通过alphac得到alpha1和alpha2?

Jasper 0

@星星星星晴哦我跟您的是一样的，我只是选取了一部分代码。您给出的这两行在alphac的定义上面，我认为作为代码层面，是不是不会返回去求alpha1和2了？

星星星星晴

@jasper-0 不好意思，这部分我不懂，我不做VOF的，只说是在createfield.H里面，alpha1和alpha2是这么定义的，而且会随着mixture.alpha1 和mixture.alpha2 的变化更新，至于具体怎么算的，你这个还要看你的solver 还有后续的过程，这只是初始化，肯定后续有计算和更新的

Jasper 0

@星星星星晴谢谢大佬了，我再继续研究一下

Tens

@jasper-0 我个人理解是这样的，createFields.H只是创建初始场，所以没必要这么准确，而在循环中的alpha1是在alphaEqn.H里直接求，alpha2=1-alpha1。

Jasper 0

@tens 谢谢您的回复，通过alphaEqn.H 发现有alphac和alpha1的关系

Tens

@jasper-0

Jasper 0

@tens 在 MPPICInterFoam 中如何通过alphac得到alpha1和alpha2? 中说：

@jasper-0

通过alphaEqn.H中的206-226行有如下代码，这几行代码应该是求解出来了乘以alphac之后的alpha1，那alpha2怎么是1-alpha1呢？不是应该alphac-alpha1吗？还望高手解答一下啊

else
        {
            alphaPhi10 = talphaPhi1Un;

            MULES::explicitSolve
            (
                alphac,
                alpha1,
                phiCN,
                alphaPhi10,
                Sp,
                (Su + divU*min(alpha1(), scalar(1)))(),
                oneField(),
                zeroField()
            );
        }

        alpha2 = 1.0 - alpha1;

        mixture.correct();
    }

Tens

@jasper-0
我的理解，alphac是颗粒的体积分数，1-alphac是连续相的体积分数，alpha1是连续相中液相占连续相的体积分数，alpha2是连续相中气相占连续相的体积分数。

Tens

@tens 睡觉前发现说反了，alphac是连续相的，1-alphac是液滴的，总之我理解的是alpha1和alpha2是占连续相的而不是总的

Jasper 0

@tens 对，所以我好奇怎么在程序中alpha2 = 1.0 - alpha1？而不是alpha2 = alphac - alpha1？

zhouxu

@tens 膜拜大佬的作息

Tens

@jasper-0 难道讲的不好理解吗
因为alpha1和alpha2是占连续相的而不是总的，连续相中只有液相或者气相，所以除了液相(alpha1)就是气相(alpha2=1-alpha1)，这个1不是总体积，而是总的连续相。
换个意思说，如果全部是占总体积的分数，颗粒为1-alphac，连续液相为alpha1*alphac，连续气相为alpha2 * alphac

Jasper 0

@tens 感谢大佬的解答！也就是说通过以下代码求得的alpha1是占连续相的体积分数？那最后结果跑出来后要想得到总的alpha1是不是要在paraview里面做计算alpha1*alphac？

 MULES::explicitSolve

            (

                alphac,

                alpha1,

                phiCN,

                alphaPhi10,

                Sp,

                (Su + divU*min(alpha1(), scalar(1)))(),

                oneField(),

                zeroField()

            );

        }

Tens

@jasper-0 是的吧

Jasper 0

@tens 多谢大佬！

Jasper 0

@jasper-0 在 MPPICInterFoam 中如何通过alphac得到alpha1和alpha2? 中说：

@tens 感谢大佬的解答！也就是说通过以下代码求得的alpha1是占连续相的体积分数？那最后结果跑出来后要想得到总的alpha1是不是要在paraview里面做计算alpha1*alphac？
 MULES::explicitSolve

            (

                alphac,

                alpha1,

                phiCN,

                alphaPhi10,

                Sp,

                (Su + divU*min(alpha1(), scalar(1)))(),

                oneField(),

                zeroField()

            );

        }

我发现interFoam中alpha1（即alpha1）的求解对应下面这个公式，

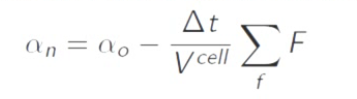
而MPPICInterFoam中通过以上代码求得的alphan为

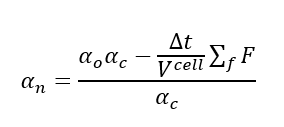
公式右边第二项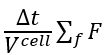是用alpha占连续相的体积分数算出来的，
而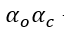和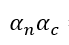都是总的相分数，

所以此方程右边第二项是不是应该乘以个alphac呢？即

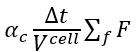
还望大佬解答一下，万分感谢！

Tens

@jasper-0 这个公式是哪里看到的，字母对应的意义不理解，在程序中相体积分数应该是通过控制方程求的吧

fvScalarMatrix alpha1Eqn
        (
            (
                LTS
              ? fv::localEulerDdtScheme<scalar>(mesh).fvmDdt(alphac, alpha1)
              : fv::EulerDdtScheme<scalar>(mesh).fvmDdt(alpha1)
            )
          + fv::gaussConvectionScheme<scalar>
            (
                mesh,
                phiCN,
                upwind<scalar>(mesh, phiCN)
            ).fvmDiv(phiCN, alpha1)
         - fvm::Sp(fvc::ddt(alphac) + fvc::div(phiCN), alpha1)
         ==
            Su + fvm::Sp(Sp + divU, alpha1)
        );

        alpha1Eqn.solve();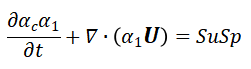

Jasper 0

@tens 这一步应该是用upwind格式求出来alpha1之后然后下面再通过MULES::correct进行修正。如果不进行修正的话，就是我之前提到的MULES::explicitSolve，在MULESTemplates.C里面定义了这个函数：

  template<class RdeltaTType, class RhoType, class SpType, class SuType>
 
  void Foam::MULES::explicitSolve
 
  (
 
      const RdeltaTType& rDeltaT,
 
      const RhoType& rho,
 
      volScalarField& psi,
 
      const surfaceScalarField& phiPsi,
 
      const SpType& Sp,
 
      const SuType& Su
 
  )
 
  {
 
      Info<< "MULES: Solving for " << psi.name() << endl;
 
   
 
      const fvMesh& mesh = psi.mesh();
 
   
 
      scalarField& psiIf = psi;
 
      const scalarField& psi0 = psi.oldTime();
 
   
 
      psiIf = 0.0;
 
      fvc::surfaceIntegrate(psiIf, phiPsi);
 
   
 
      if (mesh.moving())
 
      {
 
          psiIf =
 
          (
 
              mesh.Vsc0()().field()*rho.oldTime().field()
 
             *psi0*rDeltaT/mesh.Vsc()().field()
 
            + Su.field()
 
            - psiIf
 
          )/(rho.field()*rDeltaT - Sp.field());
 
      }
 
      else
 
      {
 
          psiIf =
 
          (
 
              rho.oldTime().field()*psi0*rDeltaT
 
            + Su.field()
 
            - psiIf
 
          )/(rho.field()*rDeltaT - Sp.field());
 
      }
 
   
 
      psi.correctBoundaryConditions();
 
  }

其中

 psiIf =
     (
         rho.oldTime().field()*psi0*rDeltaT
       + Su.field()
       - psiIf
     )/(rho.field()*rDeltaT - Sp.field());

就是我上面提到的方程
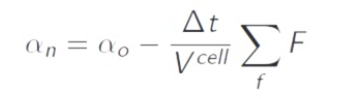
alphan应该就是最终求得的新的时间步的体积分数

Tens

@jasper-0

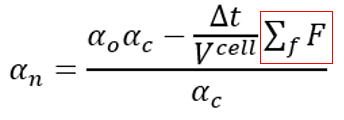
懂了，现在就是说是红色部分的问题对吧，我看了代码中这部分是通过下面代码求的

fvc::surfaceIntegrate(psiIf, phiPsi)

而里面的phiPsi则对应的这一部分

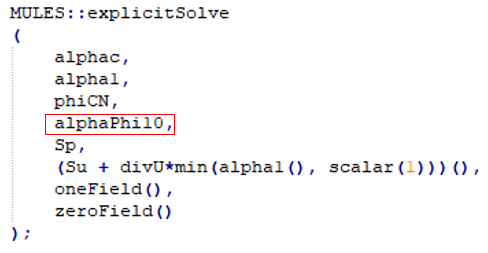
通过追踪

alphaPhi10 = talphaPhi1Un;

//又查到

tmp<surfaceScalarField> talphaPhi1Un
        (
            fvc::flux
            (
                phiCN(),
                cnCoeff*alpha1 + (1.0 - cnCoeff)*alpha1.oldTime(),
                alphaScheme
            )
          + fvc::flux
            (
               -fvc::flux(-phir, alpha2, alpharScheme),
                alpha1,
                alpharScheme
            )
        );

而其中的phiCN则

    tmp<surfaceScalarField> phiCN(alphaPhic);

    // Calculate the Crank-Nicolson off-centred volumetric flux
    if (ocCoeff > 0)
    {
        phiCN = cnCoeff*alphaPhic + (1.0 - cnCoeff)*alphaPhic.oldTime();
    }

如果不采用CN格式phiCN就等于alphaPhic，又查到

 alphacf = fvc::interpolate(alphac);
alphaPhic = alphacf*phi;

所以本质上图一中红色部分还是通过alphac*alpha1得到的

Jasper 0

@tens 懂了懂了，大佬牛！

CFD中文网

MPPICInterFoam 中如何通过alphac得到alpha1和alpha2?