Stokes流中的圆球绕流的阻力系数,怎么设置才能算准。
-
@pengdi @李东岳 感谢pengdi大佬,感谢东岳老师。您们的讨论很大程度给了我帮助,已经很大程度解答了我的疑惑。
但是!
@pengdi @李东岳 东岳老师和pengdi大佬,我觉得OpenFOAM的slip条件这里,还不能直接否定它,还不该锤它。
我想再请两位老师看看我的这个理解过程,我还拿不准一些地方理解得对不对:
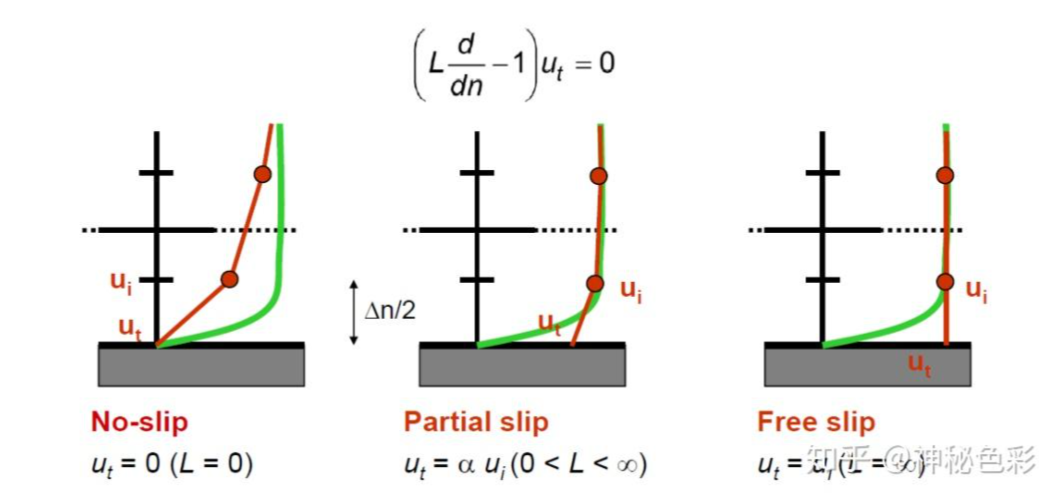
先上图:
(这个图是我自己做的,图和公式都是按照自己的理解分别拼一起的,特别是第三个切应力为0的那个表达式,我甚至觉得他写好像错了,但是我先表达一下我的逻辑和想法,请您们帮忙看看:)
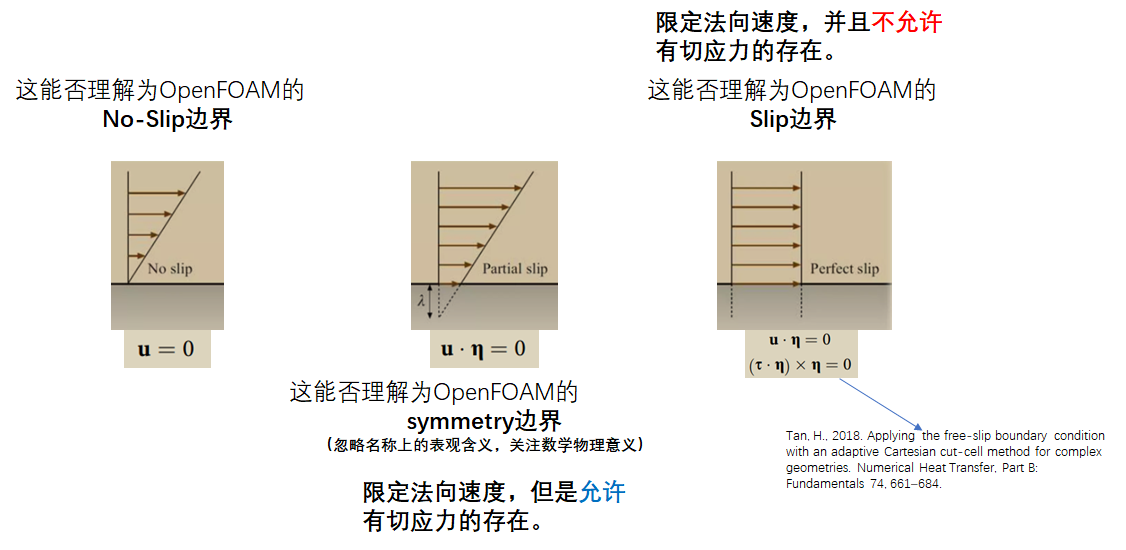
因为OpenFOAM应该内置的是:
- Slip的底层代码执行的内容是:被称为perfect-slip或free-slip的理想滑移条件(不仅要约束法向速度为0,还要约束切应力为0),这一点,OpenFOAM没有错。
- noSlip的底层代码执行的内容是:作为无滑移noSlip(界面处速度为0);这一点,OpenFOAM也没有错。
然而,我在这个帖子内提到的气泡界面“滑移”条件,虽然经常在各种文献中被大家称为“滑移slip”,但是它其实只需要一个约束条件(也就是中间这个,只约束法向速度为0,并不去约束切应力)。
不少文献将其误称为free-slip(比如常州的庞老师那篇文章....可能因为他们雷诺数比较大,然后在大雷诺数时这个边界条件带来的影响不是太明显,又或者是笔误...我很尊敬庞老师并想求签名...先在这里提前为我的comments抱歉。)但不管怎么说,这恐怕是一个错误的叫法。
因为,从下面的文献中的气泡界面法向速度分布的示意图可以看出,界面是有速度的,但是速度达不到主流速度那么大(我的同学和我讨论的结果,认为是Re=0.1时气泡界面速度大概约为主流速度的一半),因此气泡界面边界条件所指的“滑移”必然不是free-slip。
那么,符合这个帖子内提到的气泡界面“滑移”条件(也就是只约束法向速度为0,并不去约束切应力),反而是symmetry边界条件准确描述了这个问题。
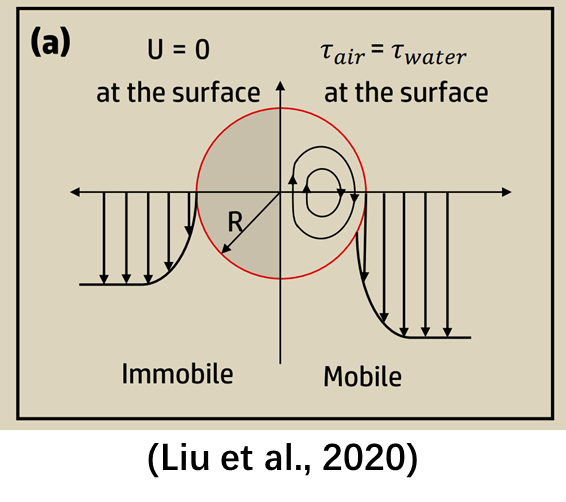
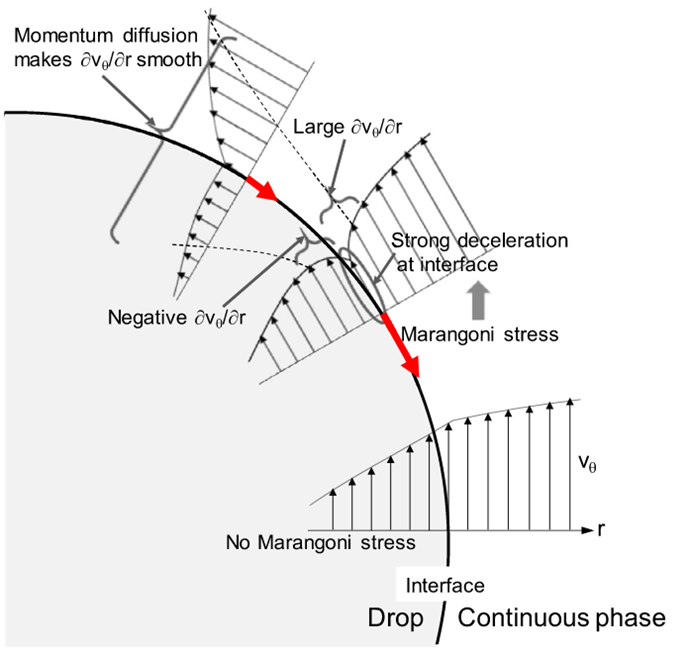
(tomiyama这个图具体是需要看最下面的No Marangoni Stress这个地方的法向速度分布图)参考文献: Liu, B., Manica, R., Xu, Z., Liu, Q., 2020. The boundary condition at the air–liquid interface and its effect on film drainage between colliding bubbles. Curr. Opin. Colloid Interface Sci. 50, 101374. Hosokawa, S., Masukura, Y., Hayashi, K., Tomiyama, A., 2017. Experimental evaluation of Marangoni stress and surfactant concentration at interface of contaminated single spherical drop using spatiotemporal filter velocimetry. Int. J. Multiphase Flow 97, 157–167.----------------------------------------分割线:回复Pengdi老师------------------------
因此@pengdi ,PengDi老师如果您需要用slip如果是free-slip,那您的仿真其实并没错。
----------------------------------------分割线:新的一些问题和想法------------------------
然后,我现在还存在的疑惑是:
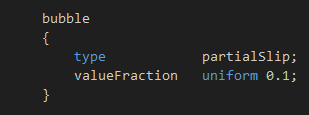
u·n=0是Partial-Slip吗?我看相关文档表示,OpenFOAM内置的Partial-Slip是继承于Slip(free-slip),然后给一个系数,感觉它主要是将界面速度执行为主流速度*系数,对于切应力方面,依然继承了切应力为0的约束条件。
因此我认为u·n=0并不是OpenFOAM中的Partial-Slip,这个观点是否正确?
再次谢谢东岳老师@李东岳 和Pengdi老师@pengdi

-
@Prometheus10 在 Stokes流中的圆球绕流的阻力系数,怎么设置才能算准。 中说:
,虽然经常在各种文献中被大家称为“滑移slip”,但是它其实只需要一个约束条件(也就是中间这个,只约束法向速度为0,并不去约束切应力)。
我认为主要是因为symmetry边界限制了法向速度,slip边界只能保证切向速度相同,但是不能限制法向速度,可能和你的观点差不多。今天我会做个算例来验证一下。是否应该限制法向速度我觉得也不太好说,可能需要结合具体的问题开展分析。
-
-
@xiezhuoyu 您好 @xiezhuoyu ,先尝试回答您的提问:
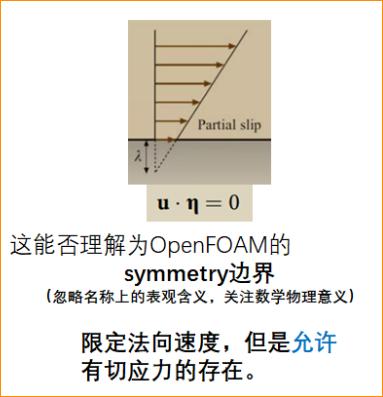
这个图带来了误解(这个图其实是partial-Slip的图,我放这个图主要是想请大家帮忙厘清下u·0和气泡“滑移界面”以及partial-Slip之间的关系)。那么,回到问题上来:
u·η=0(也就是symmetry边界的数学表达,COMSOL里可以看到对称边界的数学方程就是u·η=0)的作用是什么? 我想象对于一个气泡界面处的流体而言,施加这个u·η=0的条件,并不是约束沿气泡界面法向的速度变化,而是要求流体沿壁面“贴体”进行运动,也就是说靠近壁面处的流体,不能沿法向运动,只能沿着切向运动。
但是!切向有没有运动,需要来看切应力的大小,也就是看有没有对切应力做约束。展开来说:如果此时在u·η=0的条件上继续添加切应力为0的约束条件,那么就形成free-slip边界条件;反之,如果添加的是切应力无限大的约束条件,那么就形成noSlip边界条件(u=0)。 -
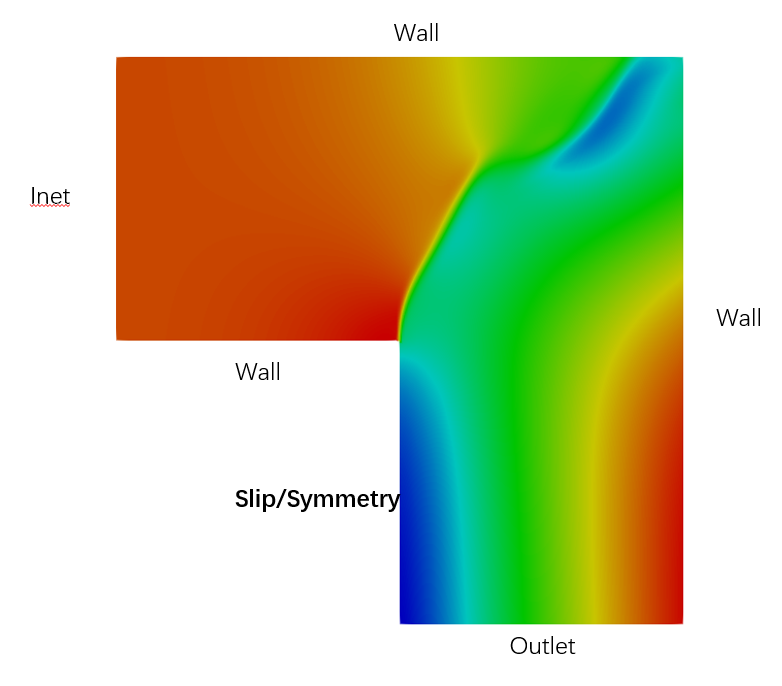
妥了,实锤了,就是slip与symmetry的问题,估计slip没有做到完全的无剪切。我这几天详细看一下
针对我上面说的,这个不对,slip可以做到无剪切。
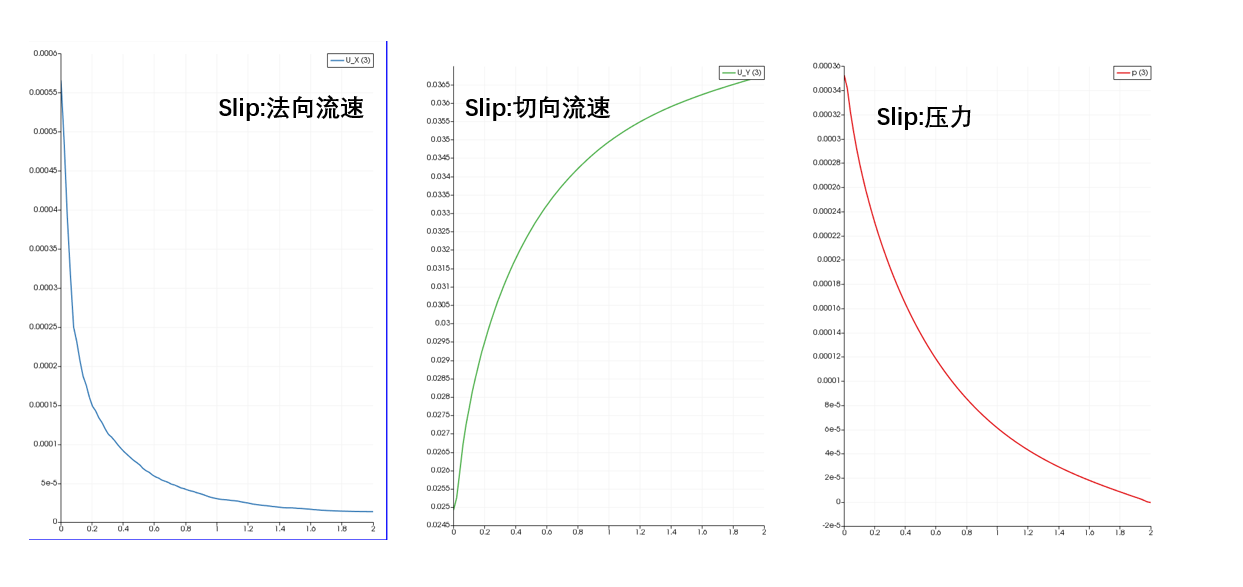
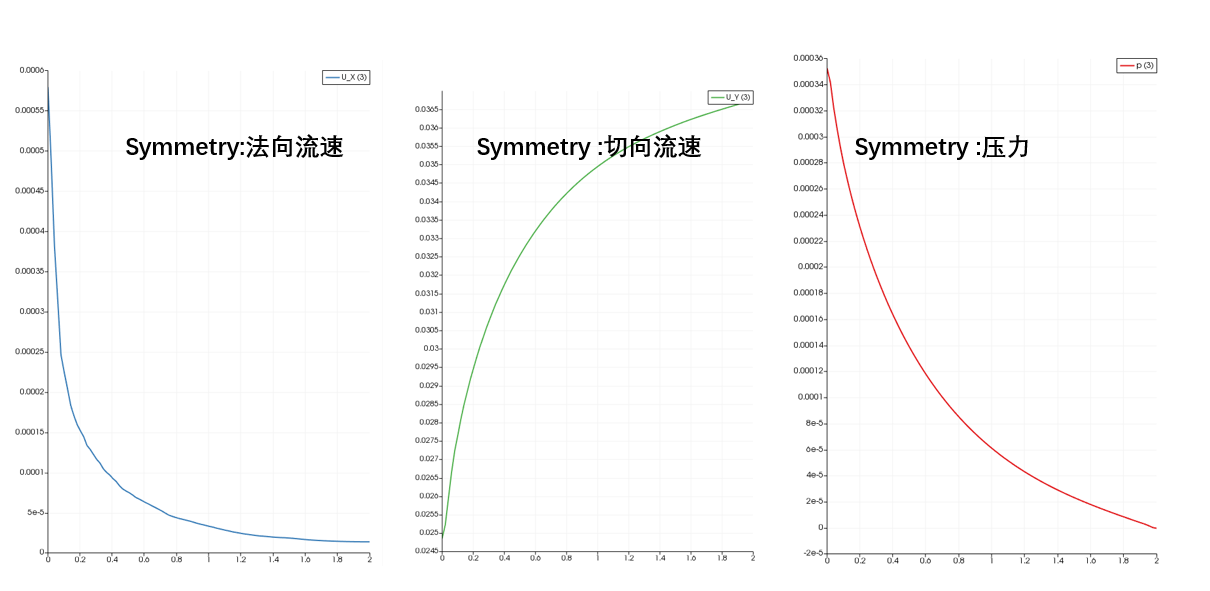
在测试算例,我尝试把球表面的值输出出来,第一个是slip,后面是symmetry:
U & n = -4.2351647e-22 max(U & n) = 4.3368087e-19 average(U & n) = -2.494512e-20 average(mag(U)) = 0.0045558926 p face value = 0.0002584113 p cell value = 0.0002584113 average(p face) = average(p) [0 2 -2 0 0 0 0] -1.1678857e-07U & n = 4.2351647e-22 max(U & n) = 4.3368087e-19 average(U & n) = -8.4957405e-21 average(mag(U)) = 0.0030605553 p face value = 0.00026689782 p cell value = 0.00026689782 average(p face) = average(p) [0 2 -2 0 0 0 0] -5.620298e-09简单嫩看出:
- 边界处slip跟symmetry的$\bfU_f\cdot\bfn_f\approx 0$,所以二者都可以把边界处法向速度限制为0。
- 压力严格的$\nabla p\cdot\bfn_f=0$,但是可以看出压力的值差距还是不小。看average(p face)这个值
- 因为slip是衍生来自symmetry,因此切向方向二者处理是一样的,都是零梯度。
所以我觉得slip与symmetry,二者都可以满足数学上的法向速度为0以及切向零梯度(在这里我不太清楚sci里面说的free slip是不是这个意思)。但是在求解的时候边界条件导致算法求解流程导致结果不一致,这体现在
average(p face)以及average(mag(U))都有差异。在求解的时候,边界条件导致算法求解流程导致结果不一致
这方面需要更详细看一下。
-
@pengdi Pengdi老师,@李东岳 东岳老师
我来补充一下低雷诺数条件下(Re=0.1时)对圆球型壁面设置为symmetry或者slip边界的切向速度的结果:
依然是Wedge楔形网格的圆球绕流文件,然后将仿真结果在Paraview中用 plotOverLine提取:首先是symmetry边界条件,第一个网格体心的速度大概是主流速度的1/2;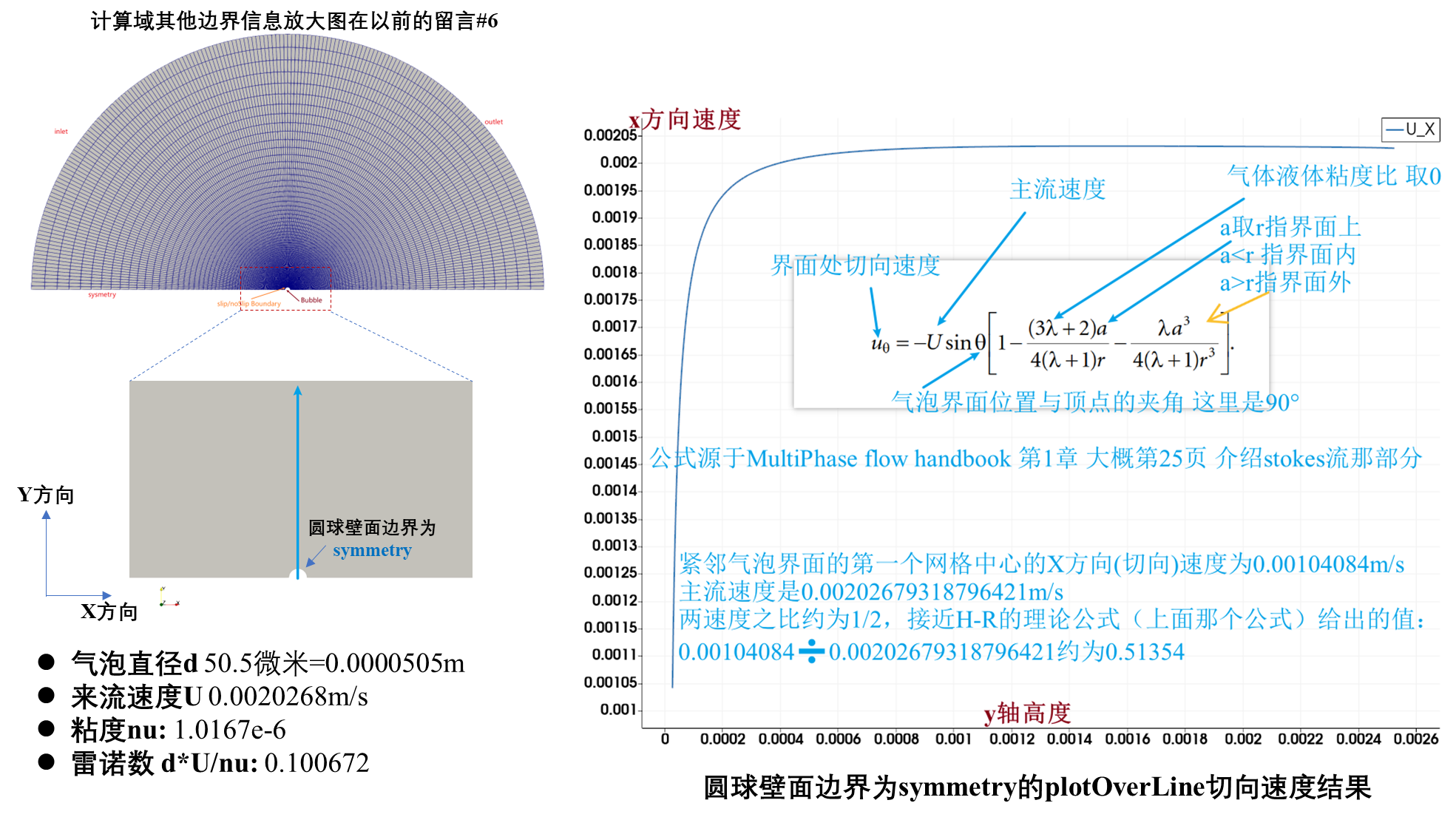
然后是slip边界条件,其第一个网格体心的速度就是主流速度;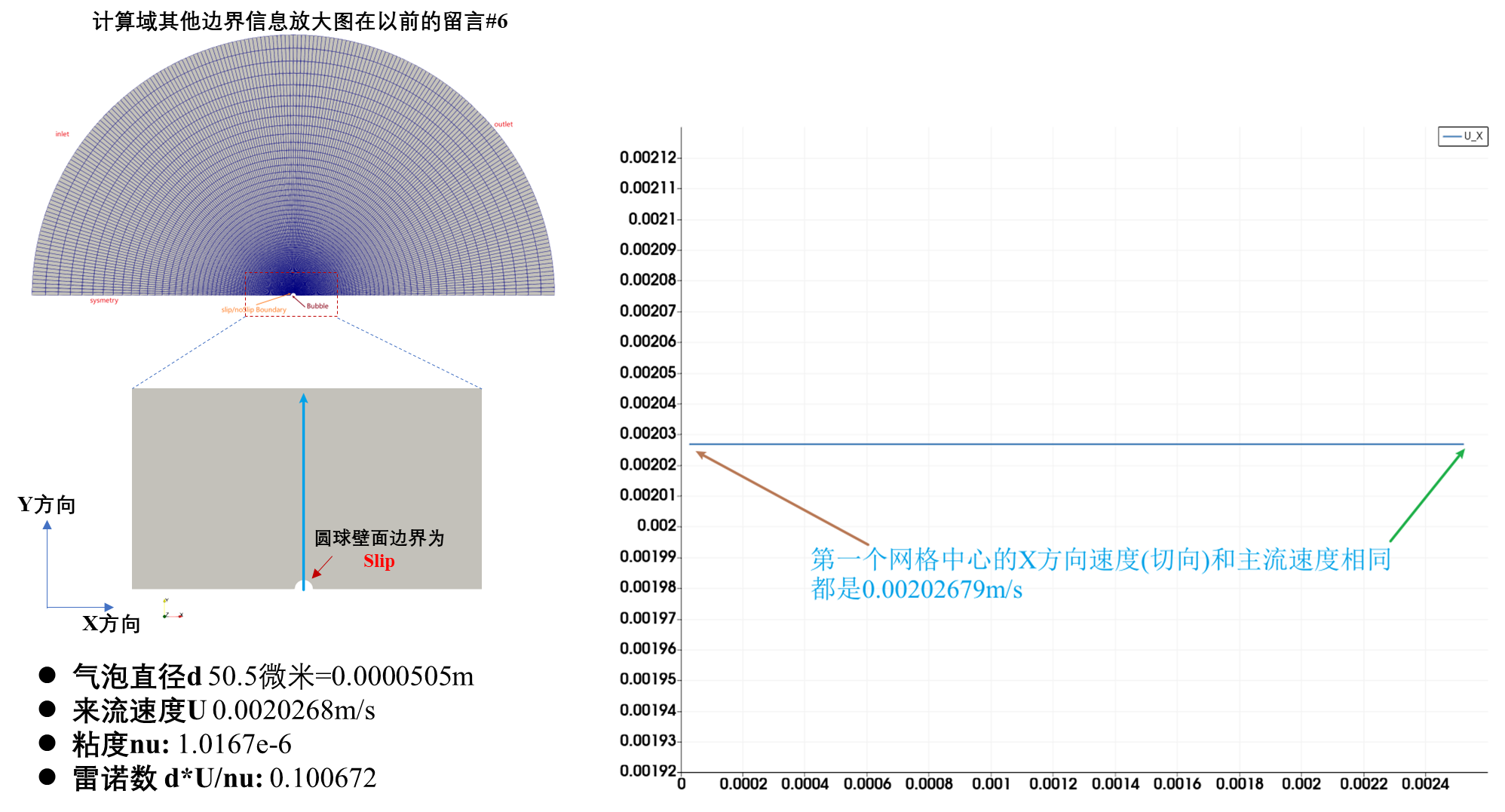
沿用一下这个示意图,symmetry边界也就是u·n=0确实很好描述了气泡界面处的速度分布,和Multiphase flow handbook第25页给出的公式也很吻合。(我这里给出的结果,准确来说,应该要说成是紧挨界面处,而不是界面上的切向速度,因为我只会用Paraview显示网格体心速度,还没能掌握如何用Info速度界面上的切向速度)

Michaelides, E., Crowe, C.T., Schwarzkopf, J.D., 2016. Multiphase flow handbook. CRC Press.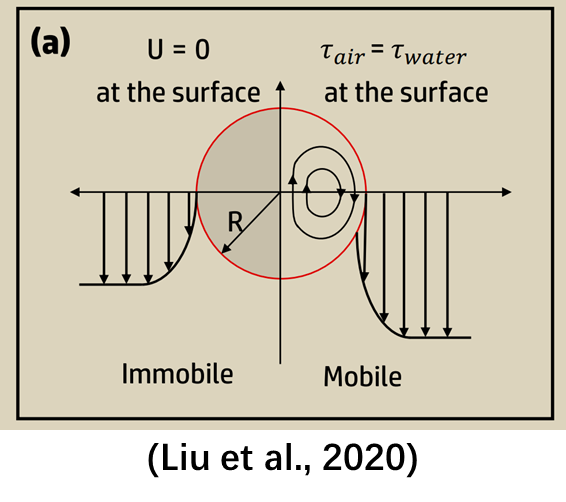
参考文献: Liu, B., Manica, R., Xu, Z., Liu, Q., 2020. The boundary condition at the air–liquid interface and its effect on film drainage between colliding bubbles. Curr. Opin. Colloid Interface Sci. 50, 101374. -
@Prometheus10 您好,关于圆柱绕流的slip和symmetry边界计算我也计算对比过,我计算的雷诺数等于200,差别确实很大。我怀疑可能正方形绕流差别就没那么大了,今天比较忙,还没验证,我看明天能不能验证一下,稍后补充上来。
-
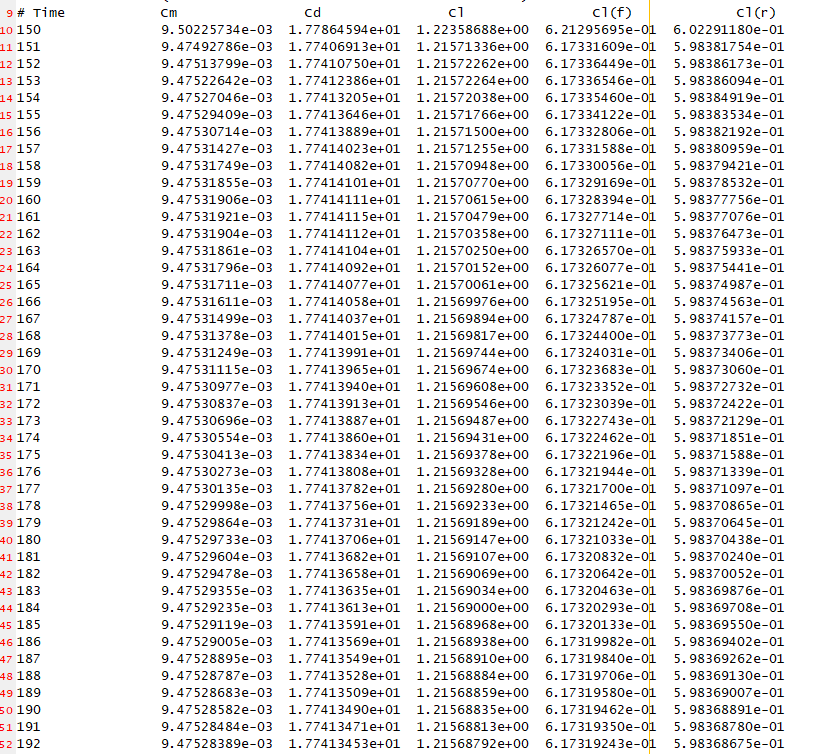
@李东岳 东岳老师好,我现在想根据运行时计算得到的Cd值的大小反过来适配速度进口的速度大小,直至阻力和浮力平衡,通过看您其他帖子,好像需要在0/U文件夹下使用codedFixedValue边界来完成,想进一步咨询您:
在codedFixedValue如何调用当前时刻的Cd?inlet { type codedFixedValue; value $internalField; name dragForceBalanceInlet; //name of new BC type code #{ const fvPatch& inletPatch = this->patch(); vectorField& vf = *this; forAll(vf, i) { scalar z = inletPatch.Cf()[i].y(); scalar rhoL = 998.13; scalar rhoG = 1.225; scalar myG = 9.81; scalar myD = 0.0000505; vf[i].x() = sqrt(4*(rhoL-rhoG)*myG*myD/(3*Cd*rhoL));//想在这里调用Cd vf[i].y() = 0.0; vf[i].z() = 0.0; } #}; codeOptions #{ -I$(LIB_SRC)/finiteVolume/lnInclude \ -I$(LIB_SRC)/meshTools/lnInclude #}; codeInclude #{ #include "fvCFD.H" #include <cmath> #include <iostream> #}; }上述代码是通过浮力和阻力的力平衡,得到阻力系数和速度的等式。
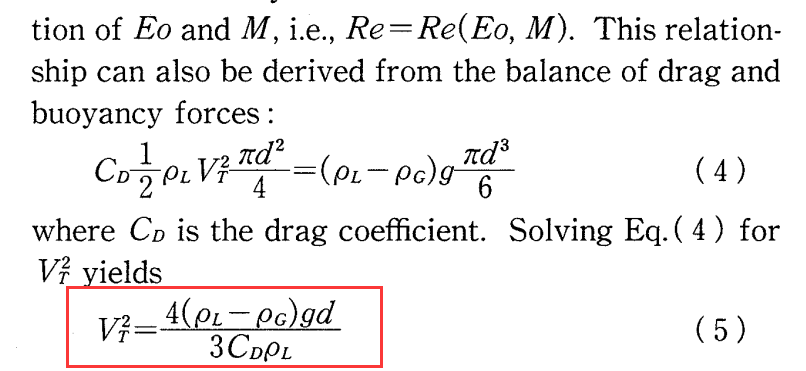
Tomiyama, A., Kataoka, I., Zun, I., Sakaguchi, T., 1998. Drag Coefficients of Single Bubbles under Normal and Micro Gravity Conditions. JSME International Journal Series B 41, 472–479.


 。
。