求助，在使用interdymfoam得到结果以后如何计算得到船舶的纵倾与横摇呢

[liujiayi]

在使用interdymfoam六自由度计算得到orientation以后然后计算得到船舶的纵倾和横摇呢

[bestucan]

你这个句子都不是很通顺啊。。。

orientation大概就是船体的朝向了。想要算纵倾和横摇得确定两个时间点吧。
两个时间点，就有两个orientation。然后就是三维空间中两条线的夹角计算。

[liujiayi]

@bestucan 在 求助，在使用interdymfoam得到结果以后如何计算得到船舶的纵倾与横摇呢 中说：

你这个句子都不是很通顺啊。。。

orientation大概就是船体的朝向了。想要算纵倾和横摇得确定两个时间点吧。
两个时间点，就有两个orientation。然后就是三维空间中两条线的夹角计算。

我的意思就是在得到了orientation的九个张量以后，如何计算出来船舶的纵倾和横倾， ，我在国外cfd网站上看到了有人用这种方式求出倾角，这么算对吗？求大佬指点。

[bestucan]

哦哦，这个是旋转矩阵。位姿控制（位置、姿态）里的内容。按说还要考虑位移。如果考虑位移就是4x4的矩阵了。在机器人控制里，多关节的机械臂末端位姿计算里会用到4x4的矩阵，如果考虑位移可以搜搜看。

如果你可以翻墙的话：图片来源

如果从矩阵得到角度也有挺多人写了代码了。可以搜搜。

[CFDngu]

@liujiayi 在 求助，在使用interdymfoam得到结果以后如何计算得到船舶的纵倾与横摇呢 中说：

@bestucan 在 求助，在使用interdymfoam得到结果以后如何计算得到船舶的纵倾与横摇呢 中说：

你这个句子都不是很通顺啊。。。

orientation大概就是船体的朝向了。想要算纵倾和横摇得确定两个时间点吧。
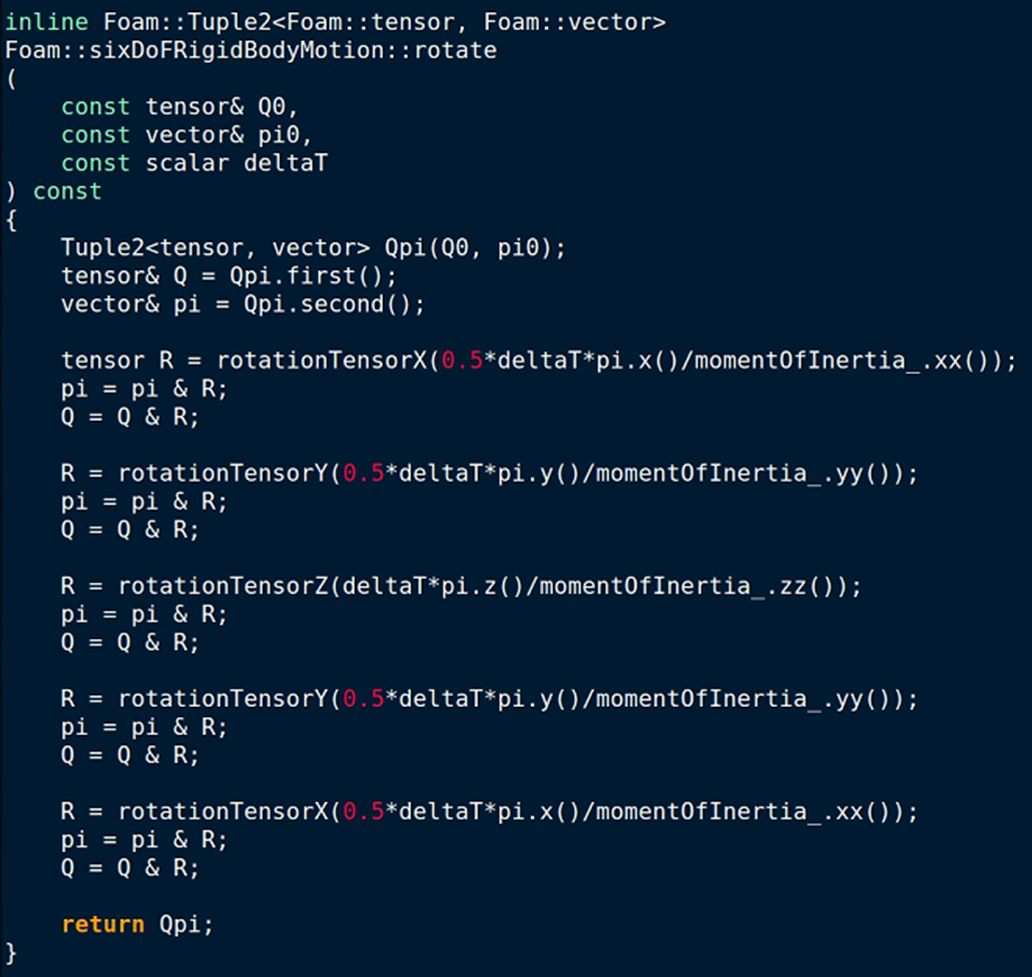
两个时间点，就有两个orientation。然后就是三维空间中两条线的夹角计算。

我的意思就是在得到了orientation的九个张量以后，如何计算出来船舶的纵倾和横倾， ，我在国外cfd网站上看到了有人用这种方式求出倾角，这么算对吗？求大佬指点。

用四元数转化，quaternion(Q()).eulerAngles(quaternion:XYZ)，大概这样

[CFDngu]

@bestucan 大佬，我借楼问一下，6DOF中的旋转为什么是这样定义的啊？没太看懂

（1）这个旋转看着不像常用的右手定则，像是左手定则？
（2）为什么要按照 0.5Rx-0.5Ry-Rz-0.5Ry-0.5Rx 这种顺序旋转？

求大佬解惑，谢谢！

[liujiayi]

@bestucan 非常感谢大佬的解释，对我非常有用

[bestucan]

@CFDngu 我看了搜了一大堆也没搞懂。但是可以明确一点。这个操作不是“把旋转分两次完成”。因为矩阵没有交换律，所以先转后转不一样，这是matlab测试代码

Rx = rotx(36);
Ry = roty(20);
Rz = rotz(80);

ori = Rx * Ry * Rz

Rx2 = rotx(18);
Ry2 = roty(10);
Rz2 = rotz(40);

split1 = Rx2 * Ry2 * Rz2 * Rz2 * Ry2 * Rx2

split2 = Rx2 * Rx2 * Ry2 * Ry2 * Rz

OUTPUT:

ori =

    0.1632   -0.9254    0.3420
    0.8316   -0.0575   -0.5523
    0.5308    0.3746    0.7602


split1 =

    0.1383   -0.8604    0.4906
    0.9844    0.0650   -0.1635
    0.1088    0.5055    0.8559


split2 =

    0.1632   -0.9254    0.3420
    0.8316   -0.0575   -0.5523
    0.5308    0.3746    0.7602

split1就是OF里的操作，和ori完全不一样。

split2和ori结果一样，因为只是旋转分成两次，而不是还交换顺序

旋转的内容好像也不是角度？pi是力矩相当于“旋转”中的力。惯性矩相当于“旋转”中的质量。力除以质量是加速度。加速度乘以时间是速度增量。当然这里的"速度"是“旋转”中的速度，即角速度。

1/2 * t * a是啥，参考匀变速运动公式，还是能找到挺多意义的。但是把这些东西乘起来。。。猜不出来。得结合更多的代码上下文看了。不过我没用过这个求解器，不太了解。

[CFDngu]

@bestucan
pi是角动量，除以转动惯量就是角速度，再乘以时间步长就是角度变化量，用来构建旋转矩阵。

最近，我又看了看相关资料，发现两处比较有意思的地方：
1、6DoF定义的orientation叫做“rotation tensor”，我查过一些资料，好像tensor的旋转和vector的旋转不太一样；
2、这个旋转矩阵应该是按照左手定则来定义的，旋转向量时，pi & R 实际上执行的是R.T()*pi，左乘转置。

上面两处是我个人的理解，不保证对。希望有大神能搞清楚这一块，指导一下，谢谢！（PS：虽然搞不清楚此处旋转为什么这样定义，但不能否认的是6DOF的计算准确性是可以的）

[bestucan]

@CFDngu 这个运算符重载真是。。。放右边结果是左乘。。。
无论是左乘还是右乘，都没有交换律。所以，应该都不是一个角度分两次旋转、旋转顺序的问题。

然后

6DoF定义的orientation叫做“rotation tensor”

这个，是因为，应该是这样的：所有船体与外界的交互，都是基于世界坐标系的。所以要把世界坐标系的力应用到船体上，就要把力之类的各种矢量张量旋转到船体坐标系去和船体交互。

还有另外一个猜测。两个坐标系之间的转换，可以通过三个旋转矩阵达到。也可以通过一个旋转轴和一个旋转矩阵达到。

我猜测，可能这个

0.5Rx-0.5Ry-Rz-0.5Ry-0.5Rx

是在组那一个旋转矩阵，或者找那一个旋转轴。如果有了这个特殊的旋转轴，那么船体的"orientation"就确实是“rotation tensor”了

以上都是我猜的_(:3」∠)_

哦，对了，这句"所以要把世界坐标系的力应用到船体上，就要把力之类的各种矢量张量旋转到船体坐标系去和船体交互。"不是猜的。是代码注释：

Angular momentum stored in body fixed reference frame. Reference orientation of the body (where Q = I) must align with the cartesian axes such that the Inertia tensor is in principle component form. Can add restraints (e.g. a spring) and constraints (e.g. motion may only be on a plane).

The time-integrator for the motion is run-time selectable with options for symplectic (explicit), Crank-Nicolson and Newmark schemes.

我应该理解对注释了吧