openfoam中伪时间步下相方程的组建和求解
-
各位老师,我想请教一下关于openfoam中求解伪时间步相方程的方法。主要计算的方程为:
$\frac{\Large \partial \alpha}{\Large \partial \tau} + t_{ext} \cdot \nabla \alpha = 0$
其中$\alpha$为相分数,$t_{ext}$为单位向量,其方向可以简单认为与$\nabla \alpha$相同,$\tau$为虚假时间步,该方程在每一真实时间步内进行空间上的推进,因此认为$\tau = k \Delta x$,k为0到1之间,如k=0.1。
计算该方程的目的是想要将VOF计算得到的两相流相分数的主相(alpha1=1)延$t_{ext}$方向进行延申。如下图所示。
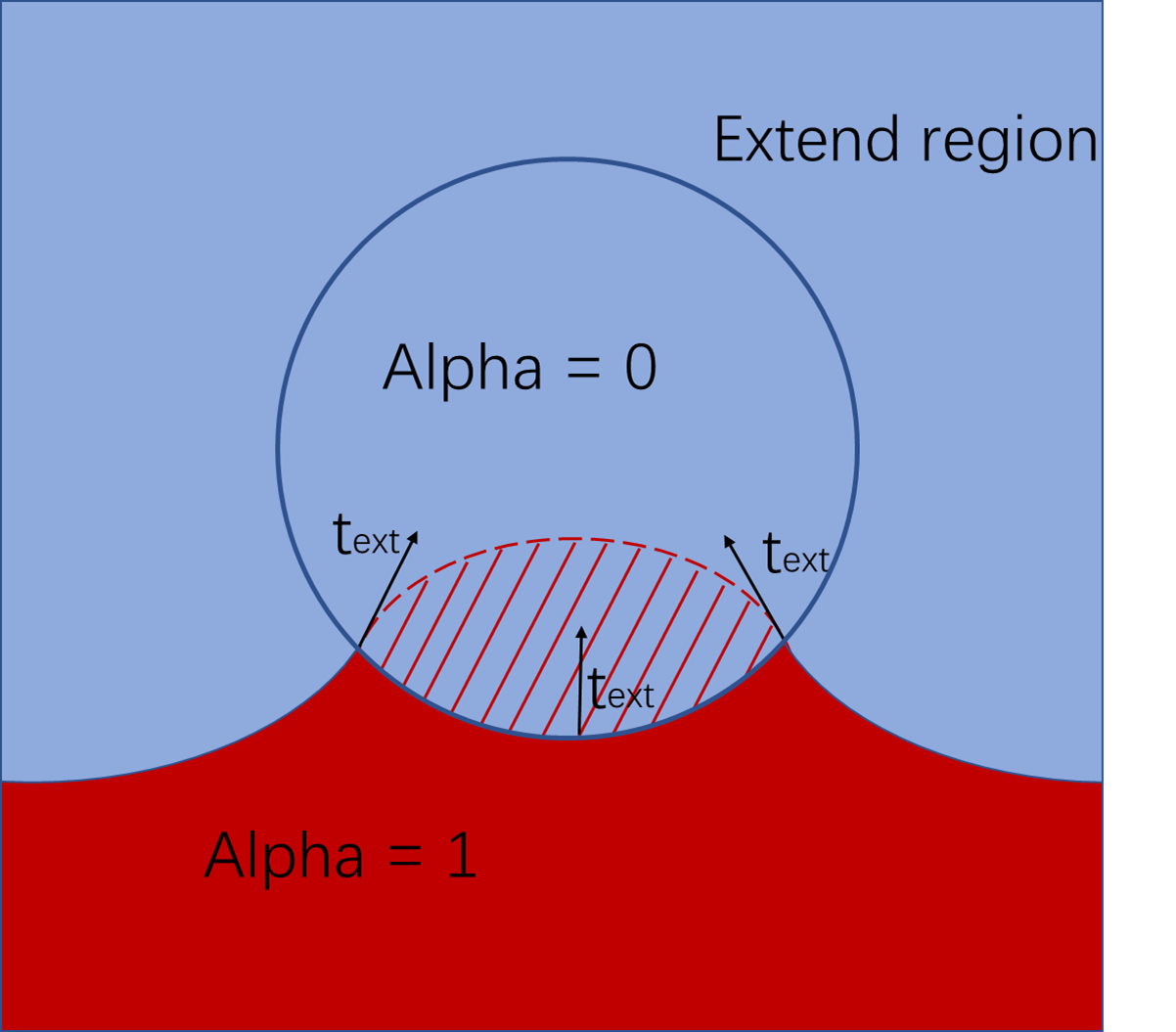
然而由于我数值求解该方程的理解有限,我使用显示计算的方法对其直接求解,并简单限制其取值范围为[0,1]。但是这种计算方法导致计算过程中,延申出来的(虚线部分)alpha表现出了局部的不连续,不光滑。有文章在该方程的基础上使用两个扩散方程对其进行光滑和反压缩,便于阅读我直接贴图,文中Eqn16即上述方程。

对此我采用最直接的方式进行显示求解,计算的效果不好,难以满足要求。
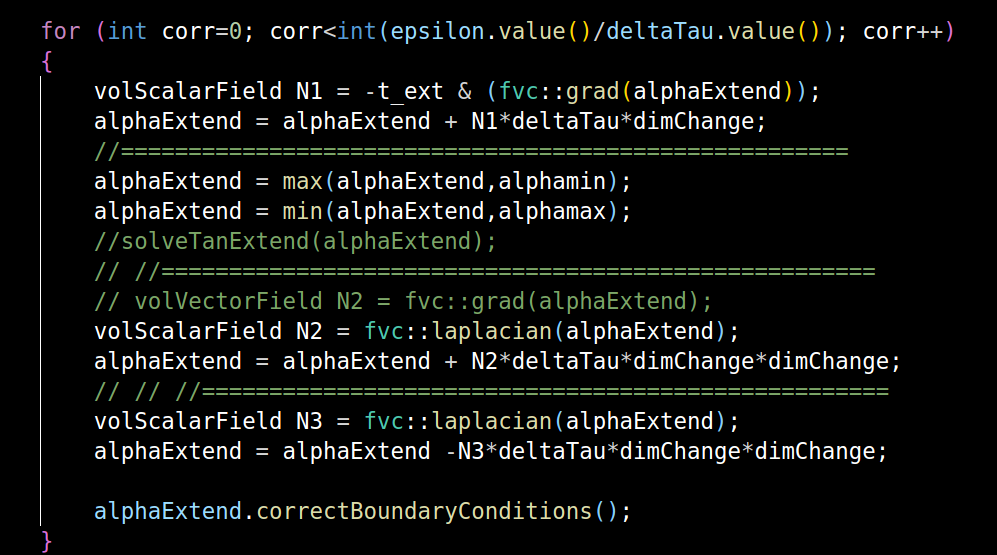
因此我想请教一下各位老师几个问题:
-
对于上述伪时间步相仿程的求解,是否有什么更好的求解方式来尽量保证计算结果的连续性以及延申之后,相界面的尖锐性。是否能直接使用MULES进行类似原本相传输方程的求解。但是这里$\nabla \cdot t_{ext} \ne 0$,我尝试进行相方程的通量构建的时候也不清楚如何对应参考,因为真实求解的相方程没有$U \cdot \nabla \alpha$这一相。请问有什么办法把这个方程使用MULES 进行求解吗?
-
对于后面提到的扩散和反扩散相,应该如何实施会更加好一点呢?虽然这两个似乎更应该用MULES求解。
-
关于MULES构建$\Sigma F$时是必须使用fvc::flux()才会有效是吗,因为limiter是跟这个通量计算方式相对应的?
-
对于我想用MULES计算是因为其使用的通量限制方法能保证计算的有界性以及精确性,我也想了解是否有其他实用有效的方式。
-
最后想问一个可能过于基础的问题,虽然也看了许多解释,但是还是想知道为什么OpenFOAM在进行一些方程计算和求解的时候总是要在面心上进行许多通量构造和积分,而许多场量的操作直接在体心上不是也能进行么?还是与有限体积的守恒性直接相关吗?
希望大家不吝赐教
谢谢大家! -
-
-
方程36是一种非常常见的对解做smooth的方法。但是方程37是一个及其不稳定的方程,看到作者求解方程37都很吃惊。方程37的对角占优特别差。只能显性求解。
-
你写的alpha对流方程肯定由于text的问题会越界。这也是一种一眼就能看出来的危险性的尝试。
-
你的$t_{ext}$就是$\bfU$。
-
正统的有限体积法是要在面心进行操作的。体心上的才需要插值过来。
-
MULES是用来处理有界性的,跟界面尖锐没有关系。扩散项也可以用MULES离散。但是这没有意义。扩散方程本来就不会产生越界问题,没有必要用MULES。
-
方程37可以用MULES来算,但是MULES是数值方法,在方程37本身就会越界的情况下,数值方法也不管用。
-
方程36求解是完全没有任何问题的,可以参考 http://dyfluid.com/rhoCentralFoam.html 直接拉到最下面,OpeNFOAM有很多类似的才做。
我最近要备课,要不可以给你详细看一下文章。目前这个阶段,如果我是审稿人的话,方程16以及方程37,我会让作者详细从数值上解释一下如何处理稳定性的。要是我做的话我会这样debug:
-
植入方程36,看结果是否是所想的,这一步证明了36植入没问题后,进行下一步:
-
植入方程36+37,看结果是否是所想的。这一步证明了36+37植入没问题后,进行下一步:
-
植入方程16、36、37,看结果是否是所想的
-
-
@李东岳 文章中对于方程37的处理应该是与这个文章中相似 https://doi.org/10.1016/j.jcp.2011.03.011
此外,对于方程16,您认为直接显示求解可行吗? -
此前也尝试植入APT文献中的那个模型,但是结果非常不好,这个日本小组的其他文章中的结果也无法复现;自己尝试改进了该模型,效果有所改进,但是仍然不够理想,不知道Chen同学是否高效解决了气-液界面外推至固体颗粒内部的问题,希望进一步讨论与交流。
-
@capillaryFix 您好,我刚刚认真看了您的两篇文章,打算参考您的光滑方式结合半拉格朗日方法试试看?日本小组的文章中结果确实很好,我个人能力有限,当时也没有复现出来,包括解析方法的表面张力的引入。后面我使用别的方法考虑接触角的准确性,暂时忽略了表面张力对颗粒的作用,也就暂时停止了这种外推的计算。
-
@Shihang-Chen 感谢回复,我最近也在继续改进这种数值外推的方法,后续有好的结果,会分享在这里。
-
@capillaryFix 好的,太感谢了,希望有机会跟您进行广泛交流
-
@Shihang-Chen
你好,我在做类似的代码。想请教伪时间步植入后,计算结果中出现松弛要怎么处理(计算的周期和实际周期不一致)。我是在动量方程中加入的隐式伪时间步。

