DEM和DPM

[.J.]

@hurricane007 那就关注一下他们近期是否会出这个功能吧

[hurricane007]

@.J. 嗯~谢谢啦

[散漫守望2016]

@hurricane007 OpenFOAM的DPMFoam我添加过化学反应，不是很难的。你好好关注一下lagrangian/intermediate库。

[散漫守望2016]

@.J. 讲解的很透彻，应该就是这样的。

[.J.]

@散漫守望2016 DEM方面和散漫学习了不少，还得你多指教。

[hurricane007]

@散漫守望2016 想到一个很蠢问题，添加化学反应首先应该要把DPMFoam加上能量方程？因为我用的是高温，气体温度估计从100度到600度变化，所以需要可压求解器？然后最近在做这一步都感觉好难。。。

[李东岳]

@hurricane007
我对DEM算法不是很熟悉，不过我在单相流和多相流中添加过单向耦合的粒子。如果你需要耦合，无非就是在DPMFoam类求解器下添加反应和能量，要么就是在反应和能量求解器中添加粒子。我看你目前的做法是基于DPMFoam添加反应和能量，是否可以换一种思路？比如在reactingFoam里面添加粒子。

[arctan]

搭车问一下fluent DPM-Laws for Heat and Mass Exchange 的参考文献是什么？或者有没有相关的Eulerian-Lagrangian好书推荐？

[OF九月九]

我觉得这本书不错Multiphase Flows with Droplets and Particles (Second Edition)-Clayton T. Crowe，网上有电子版，里面介绍离子的受力运动和粒子传热相变比较详细。

[arctan]

@OF九月九 多谢，这本书我也在看，确实很不错，但是 Fluent DPM 的原始出处似乎不是这里。

[李东岳]

这个帖子发出来2年多，2015年的这个时候我主要做欧拉欧拉模型，2017年年初开始做一种欧拉欧拉和欧拉拉格朗日的混合方法，最近转了纯欧拉拉格朗日，加深了一点理解。

多相系统

欧拉欧拉和欧拉拉格朗日主要用于描述多相系统，欧拉欧拉是两相均用欧拉NS方程描述，欧拉拉格朗日是一相用欧拉，一相用拉格朗日方程描述。对于两相系统，欧拉欧拉方法模型为双流体模型（Two fluid model，TFM），欧拉拉格朗日方法为Discrete Particle Model（DPM）。

从数学形式上，DPM的控制方程要比TFM中的离散相方程简单，比如这个是DPM中描述粒子的速度方程（牛顿第二定律）：
\begin{equation}\label{DPM1}
m\frac{\mathrm{d}\mathbf{U}}{\mathrm{d}t}=\mathbf{F}
\end{equation}
\begin{equation}\label{DPM2}
\frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}=\mathbf{U}
\end{equation}
这个是描述粒子的欧拉方程（2018.01.04更新：经石油大学某同学建议改正符号错误）：
\begin{equation}\label{TFM1}
\frac{\partial \alpha\mathbf{U}}{\partial t}+\nabla\cdot\left(\alpha\mathbf{U}\mathbf{U} \right )-\nabla\cdot\tau=-\alpha\nabla p+\mathbf{g}+\mathbf{M}
\end{equation}
\begin{equation}\label{TFM2}
\frac{\partial \alpha}{\partial t}+\nabla\cdot\left(\alpha\mathbf{U} \right )=0
\end{equation}
很明显，拉格朗日方程是一个单纯的ODE，在将方程右边某些力简化的情况下，这个ODE是存在解析解的。欧拉方程需要数值求解，并且耗散性比较严重。

如果只是单纯的求解方程\eqref{DPM1}和\eqref{DPM2}，你都不需要网格，直接求解就可以，这只是单纯的ODE。

个人感觉TFM要比DPM的求解数值上问题比较多，比如比较出名的相分数有界、高梯度区域力的模化、相分离导致的奇异、高阶格式震荡等等等等。DPM都不存在这些问题。

但是如果看DPM的算法，如何跟踪粒子的位置信息占据了大头。目前的算法，即使将网格拆分成为四面体，依然会发生粒子丢失的现象，在某些网格较差的情况下，会陷入死循环。

求解器不发散，就是一直loop :big_mouth:

DPM，DEM，MPPIC

在考虑多相流的情况下，一般颗粒相用方程\eqref{DPM1}和\eqref{DPM2}来描述，连续相用NS方程来描述，也就是同时求解\eqref{DPM1}，\eqref{DPM2}，\eqref{TFM1}和\eqref{TFM2}。

同时求解这四个方程最重要的问题就是效率问题。

1. 求解不需要网格的ODE方程需要高效的处理粒子跟踪位置问题，这个问题处理不好很容易导致粒子算着算着丢失了。一个一个粒子去找当然可以，但是如果有10e7个粒子肯定没办法处理。在OpenFOAM中，通过将网格四面体化来处理，由于商软代码不开源，不知道商软如何处理粒子位置跟踪的效率问题。

2. 粒子间作用力的处理，在这里，如果考虑OpenFOAM中的DPM模型（商软中的DPM不清楚是否也是这样），方程\eqref{DPM1}中右边的力主要包含了曳力、虚拟质量力等非常主要的力。但是在DEM中，除了上述的力，还有旋转、摩擦、凝聚等，比较重要的颗粒碰撞也通过软球模型来处理（下图是google随便找的）。
   
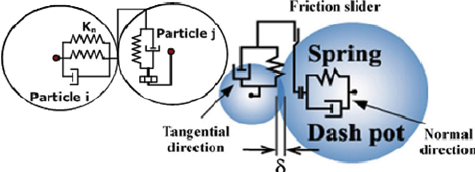
   所以说，DEM 处理的力更加全面，并且在DEM中对于颗粒的形状也会进行考虑，形状会进一步影响力的作用。

3. MPPIC是为了更加的追求高效的一套算法。在MPPIC中，多个particle被打包到一起并被称之为parcel，在计算parcel运动的同时，插值出欧拉场。欧拉场的作用在于在MPPIC的控制方程中添加一个固相应力。在TFM中，也存在这样一个固相应力，因为TFM是欧拉框架下的。也就是说，MPPIC中，碰撞模型通过欧拉场的固相应力进行表征。为什么这么做？大量的节省用于计算颗粒碰撞导致特别小的时间步长。这在OpenFOAM的代码中很直接的表现出来：

   #ifdef MPPIC
   #include "basicKinematicMPPICCloud.H"
   #define basicKinematicTypeCloud basicKinematicMPPICCloud
   #else
   #include "basicKinematicCollidingCloud.H"
   #define basicKinematicTypeCloud basicKinematicCollidingCloud
   #endif
   

   如果是MPPIC方法，调用MPPIC的碰撞模型（basicKinematicMPPICCloud.H），如果是DPM，调用碰撞模型（basicKinematicCollidingCloud.H）。

Misleading

另外好像现在各大厂里面的各种算法虽然是一个名字，但是使用的算法不同，比如按照 @散漫守望2016 所说：

Fluent中的DPM模型只能处理稀相的气固（气液）两相流，一般我们称它为“双向耦合”，颗粒颗粒间不发生碰撞以及在流体方程中不考虑空隙率。

但是在OpenFOAM中的DPMFoam也可以处理碰撞以及体积分数耦合问题。同时DPMFoam也可以使用DEM中的软球模型，虽然他被叫成了DPMFoam，并且DPMFoam也可以调用MPPIC中parcel的概念。据我所知，parcel这个概念最早出现在Andrews and O'Rourke 1995年的文章中。

同时，MPPIC在ANSYS Fluent中被称之为DDPM，在称之为CPFD。

---

最近我在用欧拉拉格朗日和精确解对比然后模拟3D鼓泡床 :cheeky:

[hurricane007]

东岳兄这个回复很详细，我有一些补充。

1. 我感觉DPM的控制方程虽然是个ODE，但是在运算的过程中其实 F 是在变的，理论上说解析解存在，但是在一个实际系统里面由于F在变，所以其实并没有意义。
2. 跟踪粒子的位置信息占了大头，其实应该说是碰撞探测占了大头，在MPPIC里面也跟踪粒子，但是速度快得多；
3. MPPIC 高效在用一个 solid stress 来模拟碰撞，因此不需要确定颗粒碰撞了，这一点省了很多时间，对于parcel 用一个点来跟踪多个颗粒，在DPM也有做，叫做coarsed grain DPM； 但是做parcel都需要一个子模型来模拟这个parcel的行为，我测试下来，对于一个 N 颗粒系统，如果一个parcel包含nParcel 个颗粒，那么 计算时间的比值大概是 T(single particle) / T(parcel) = (nParcel)^1/3 。

[马乔]

coarsed grain DPM如果不考虑切向力的话，也可以算作MP-PIC呀，参考Patankar2001。solid stress有点类似于TFM了；solid stress虽然有点用（阻止颗粒过度堆积），但是速度修正才是最关键的。parcel的问题，于是用了daming 和isotropy来解释颗粒碰撞问题。

[马乔]

fluent DDPM 用的是Lun的应力模型（TFM），CPFD用的是Harris的。先想到这么多，以后想到再补充。

[hurricane007]

@马乔 MPPIC 精髓还是在于那个solid stress 来模拟particle-particle force，而DPM/DEM 要直接计算颗粒间作用力。我觉得MP-PIC 在某种程度上是 "TFM DPM 混合"的方法，TFM来算 particle particle force，DPM 来追踪颗粒。而 Coarsed grain DPM 最初的概念是 particle-particle force 用大颗粒算，gas-particle force 用小颗粒算，似乎和PIC也没有关系啊。但是到后面发现 1. 一堆小颗粒在一起应该会“变软”；2. 转动惯量（也就是切向力）有影响，还有一些不记得了，所以后面就加了一些修正了，当然可能后面也有用PIC的思想来修正的

[马乔]

只要是个在thetacp点附近能阶跃的函数都可以用来做solid stress，后面的速度限制很重要。嗯，我对比了不同的应力模型。网格四面体化来进行LPT以及向前向后映射在非结构网格上很有用，虽然也可以用多面体插值。网格四面体化还可以配合不同的空间分解形式。额，这个我也对比了下，效果还不错。

[李东岳]

ANSYS Fluent或者Barracuda里面颗粒跟踪怎么处理的？

[马乔]

LPT主要的是建立网格与粒子间的联系，比如某一时刻属于哪个网格，在网格单元内相对于中心点的位置是怎么样的，这个能决定插值权重，至于它怎么移动，不用care的。因此，对于bar这样用笛卡尔网格的，粒子定位简直太简单了，直接定位就行，所以不用操心。所以大部分做LPT的还是用笛卡尔网格的好。至于fluent，它不是只认非结构网格么？感觉OF在很多方面都在像fluent学习耶。。
还有为嘛这么容易断开连接啊

[yuanlee2011]

@散漫守望2016 最近想对DPMFoam求解器进行一些修改，添加一个标量p_t来描述颗粒温度变化（之前基于particle class类实现过），由于对intergrangian/intermediate库结构不太了解，对其修改过程中总是出现各种错误，知道你对intermediate库有比较透彻的认识与理解，想问问有没有好的参考资料或者建议，望不吝赐教，非常感谢！

[yuan]

关于在 DPMFoam 添加化学反应，CFD Online 上有一个关于 coalCollidingChemistryFoam 的讨论（https://www.cfd-online.com/Forums/openfoam-programming-development/158458-colliding-coal-cloud-coalcollidingchemistryfoam.html ）， 即在煤燃烧的算例中添加 DPMFoam 中碰撞项的处理。在该帖子中提供的求解器可以在 OpenFOAM 2.3.x 版本中编译并运行。

但是对该模型中添加 submodel 的部分不太理解，直接将该方法用于向 MPPICFoam 中添加化学反应则一直失败。不知道有没有人有类似需求的，是否可以讨论下？