自适应网格优化 求助！！!

[韬光养晦]

基于2011年发表在Journal of Computational Physics的文章Adaptive mesh refinement based on high order finite difference WENO scheme for multi-scale simulations，并根据您文章的网格自适应算法编写了一套计算程序，在计算双马赫反射算例过程中，遇到了一些问题，受困许久，希望大神指点迷津~ 在此诚挚感谢
遇到的问题具体问题如下：
在计算双马赫反射问题时，在Kelvin-Helmholtz rolls两侧流场出现较大的震荡，局部密度云图及网格自适应加密情况如图1所示，震荡区域存在粗细网格过渡,故怀疑在粗细网格过渡中存在算法错误或者代码错误（我已多次检查代码，未发现代码错误，但不能完全排除仍有代码错误存在）。

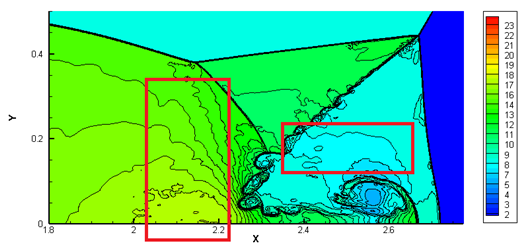
（a）局部密度云图（红框处为存在流场震荡处）

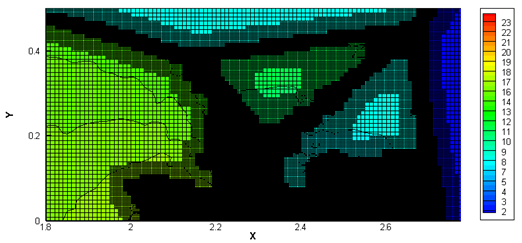
（b）局部网格生成

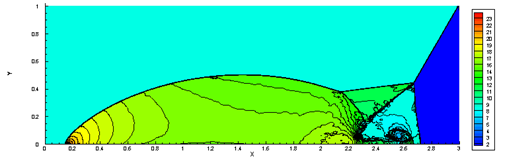
（c）总体密度云图

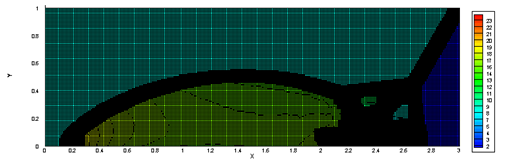
（d）总体网格生成（黑色区域表示网格加密）
图1 局部密度云图及网格自适应加密情况
该程序采用C++语言编写，流场计算使用有限差分法，五阶WENO格式，Steger-Warming通量分裂，2D欧拉方程，时间推进采用3阶Runge-Kutta方法；网格自适应加密方法和加密准则与您的论文有所不同，采用基于原始根网格进行加密，每个网格单元生成3×3个子网格单元，加密准则使用密度梯度(∂ρ⁄(∂x+∂ρ⁄∂y))。一共使用三层网格，在计算域[0,3]×[0,1]中，原始根网格单元数量为300×100。Layer 0表示原始根网格，Layer 2表示最密的网格。Layer 2比Layer 1略大，覆盖Layer 1，两层网格的间隙为3个根网格单元的尺度，如图2所示。以此希望精准捕捉激波，并适当减少网格生成数量。子网格层的时间步长为父网格层的1/3。
父网格层每计算完一步，对父网格节守恒量（ρ，ρu，ρv，E）和守恒量对时间的导数[ρ’，（ρu）’，(ρv)’，E’]进行五阶加权(类似WENO加权)空间插值，求解出子网格层边界的虚网格节点的相应守恒量及其导数。并将前一时间步和本时间步插值出的通量及通量导数使用Hermite插值，以获得三个子时间步的相应变量，作为加密网格层的边界条件，并使用式（1）作为Runge-Kutta时间推进的中间步的边界条件。

在子网格层三个时间步计算完成后，父网格层被子网格层覆盖的节点数值被子网格对应同位置节点更新。每一或两个根网格时间步重新生成一次加密网格。

（a）粗网格和细网格

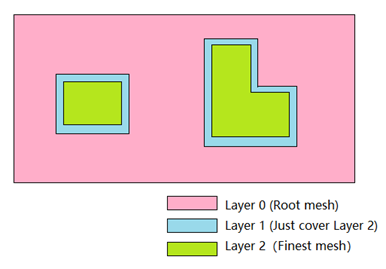
b）不同层次网格
图2 网格加密示意图
其他相关的情况介绍：
在一次测试中使网格只加密，不减少，结果显示流场基本没有前述震荡，结果如图3所示。此算例应该可以证明该程序计算格式是正确的。然而，由于生成网格实在太多，不具实际应用意义。

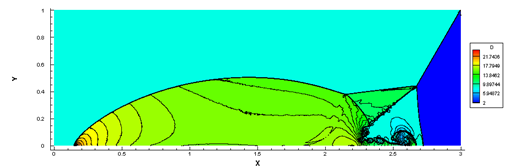
（a）密度云图

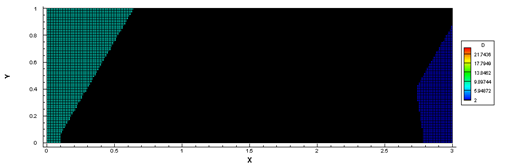
（b）网格生成情况（黑色为加密区域）
图3 网格只加密不减少的计算结果

不知大家在调试程序过程中，是否遇到过类似的情况。
希望大家能够指出
（1）我对算法的理解是否存在错误，特别是粗细网格过渡部分的算法；
（2）解决该问题有何建议；
（3）能够告知粗细网格过渡区域，造成的流场震荡的原因可能有哪些;

再次感谢大家！