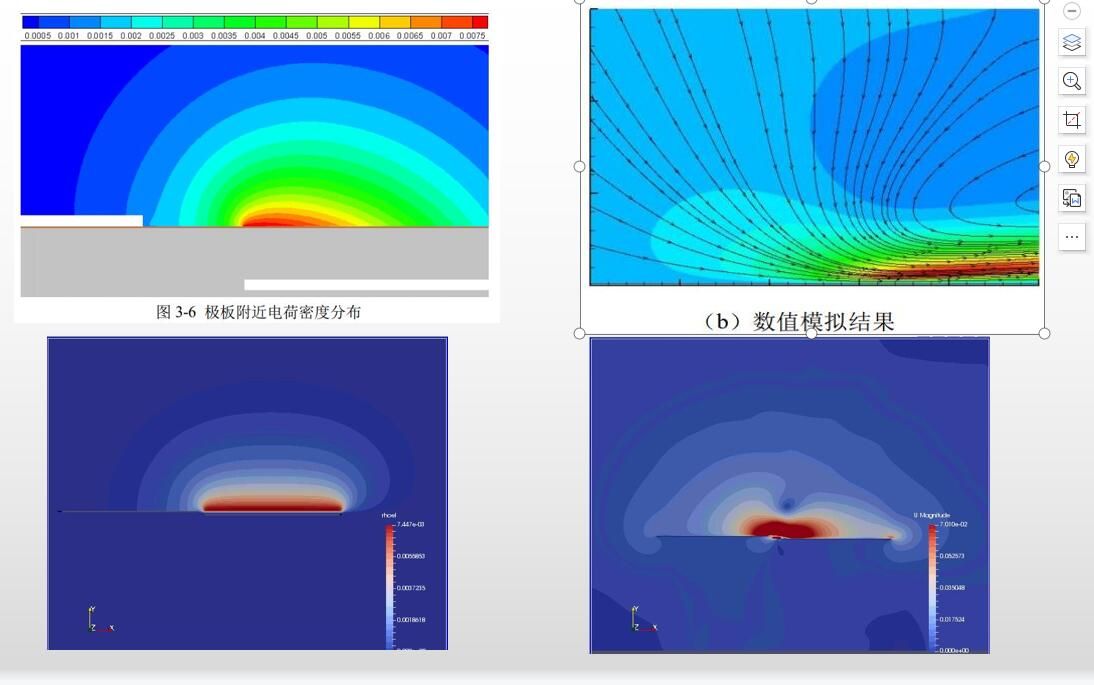
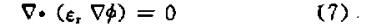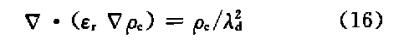求助:孔隙介质中流体被加热上浮过程的压力方程求解问题
-
首先非常感谢东岳老师回复答疑!估计李老师您对海底黑烟囱也有了解的,这个问题其实就是模拟seafloor hydrothermal circulation(海水通过洋壳的孔隙和裂隙下渗至深部被岩浆房等热源加热,密度变小,在上浮作用力下最终喷出至海底)。
(一)$\phi$表示孔隙度是常数;$\alpha$和$\beta$分别表示热膨胀系数和压缩系数,虽然是温度和压力的函数,可以用相应的理论和公式计算出来,这里可以简化认为是个常数。
(二)确实还有一个连续性方程的(如下公式4),这几个方程和这个nature文章的method部分的公式3,4,5,6对应的。
\begin{equation}
\frac{{\partial \phi \rho }}{{\partial t}} = - \nabla \cdot \left( {\vec u\rho } \right)
\end{equation}方程(2)也就是压力方程,是将达西速度带入这个连续性方程,然后对密度^\rho^求了对温度^T^和压力^P^的全导数得来的。
-
@东岳
我查了一些资料和东岳流体网站上的一些solver的讲解,这个问题是不是得用这个PIMPLE算法求解,但是不确定努力的方向是否正确 -
从Nature的文藏来看:
-
求解压力方程:
\begin{equation}
\nabla \cdot \left( {\frac{{k\rho }}{\mu }\left( {\nabla P - \rho \vec g} \right)} \right) = \phi \frac{\partial \rho}{\partial t}
\end{equation} -
求解速度方程:
\begin{equation}
\vec u = - \frac{k}{\mu }\left( {\nabla P - \rho \vec g} \right)
\end{equation} -
求解温度方程
明天再详细看看,
你在研究Nature么 有前途..
有前途.. -
-
@东岳
太感谢了!我博士论文就是做这个流体循环并且耦合矿物反应的模拟,目前我们用的是有限元方法, 我从您的网站和论坛上了解到有限体积法和openfoam,感觉这个更有意思。所以我想用openfoam尝试做后面的模拟任务。您的意思是说直接求解方程(8)表示的这个压力方程对吧?可否推荐一个相似的solver的求解过程或者其他相似的资料给我参考一下。看了buoyantPimpleFoam的求解跟我这个问题最相近,但是它的求解方程式N-S方程,我这个问题应该是NS方程的一个简化形式。我尝试根据您的指导把代码写出来,再请教您
-
@东岳
我这里的流体是水(water),不可压缩。密度是变化的,$\rho=\rho(T,P)$,可以通过IAPWS方程求解得到,简化认为是温度的线性函数。




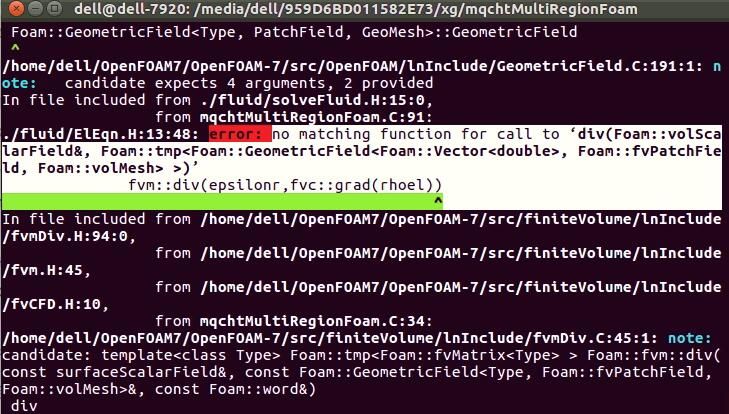


 ,问题解决,OF小白一只,多多包涵
,问题解决,OF小白一只,多多包涵