有没有人可以讨论一下von Neumann stability analysis?
-
我最近又被这个卡了一下。不过比去年好一些了。
以一阶线性对流方程为例:
$$
\dfrac{\partial{u}}{\partial{t}}+U\dfrac{\partial{u}}{\partial{x}}=0
$$半隐式方法,变成ODE
$$
\dfrac{\partial{u}}{\partial{t}}+U\dfrac{u_{i+1}-u_{i-1}}{2\times\Delta{x}}=0
$$全隐式方法,变成代数方程。
$$
\dfrac{u^{n+1}{i}-u^{n}{i}}{}+U\dfrac{u_{i+1}-u_{i-1}}{2\times{\Delta{x}} = 0
$$这些分析方法,有没有大神对这个很了解的?有很多困惑没办法解决!
-
@东岳 我不能预览,只能手打。
好痛苦。不知道怎么解决这个问题。
-
@东岳 $ \dfrac{u^{n+1}_ {i}-u^{n}_ {i}}{\Delta{x}}+U\dfrac{u_{i+1}-u_{i-1}}{2\Delta{x}} = 0$
-
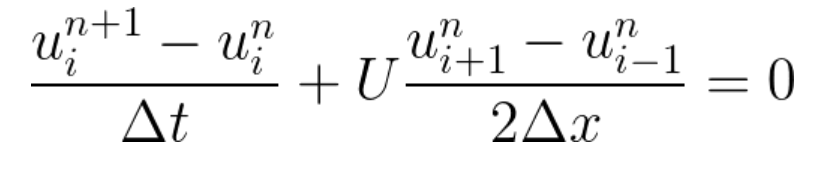
一个公式真是折腾死了。
我看了好几个人讲关于von Neumann稳定性分析。
- 12步入门Python这个女老师讲的。
- MIT qiqi wang讲的PDE课程
还是有些地方很模糊。
