关于动网格的求解方法及步骤咨询

winsway_zero

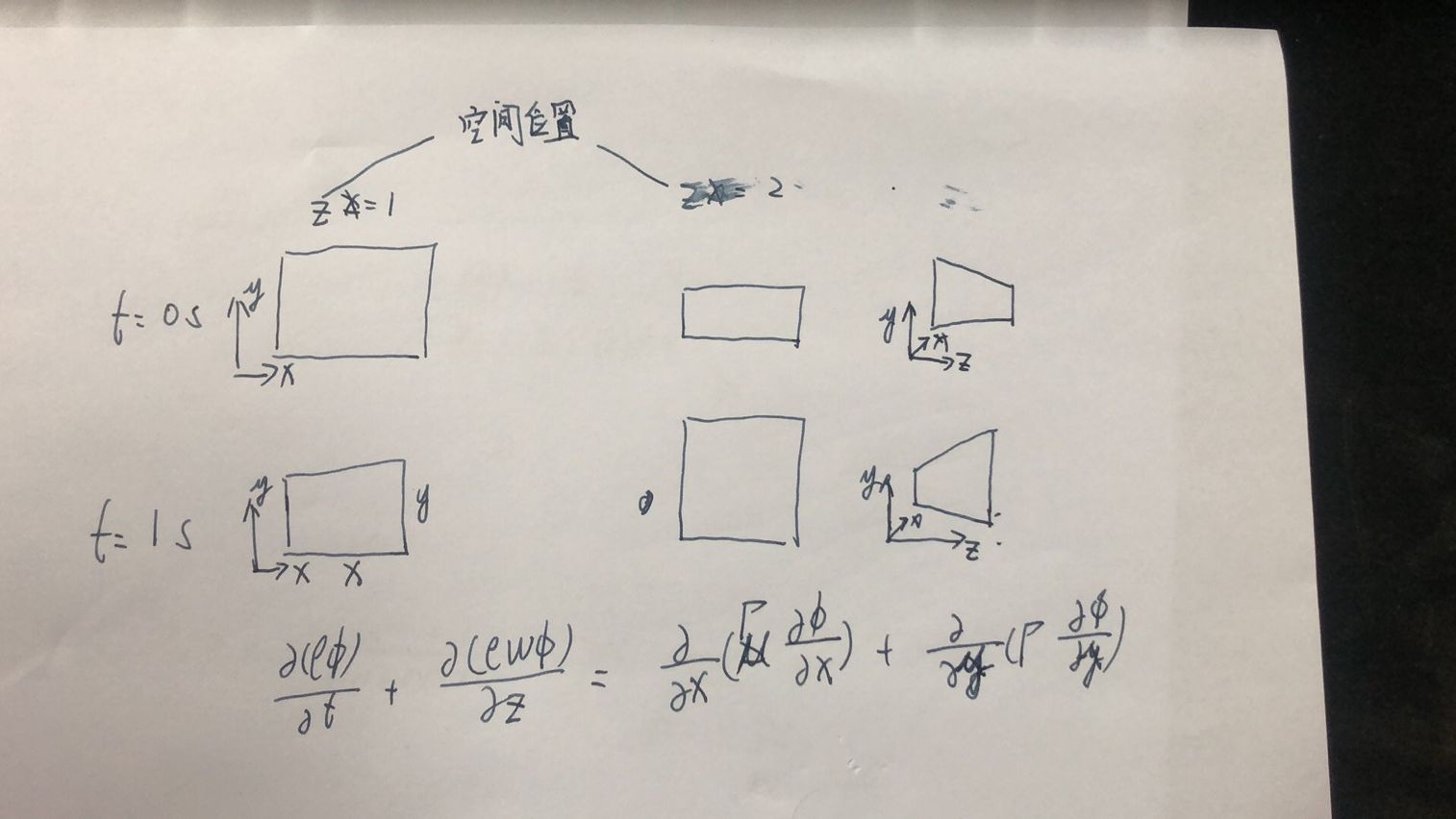
想咨询一下动网格的控制方程应该如何处理呀；控制方程里面忽略了X,Y方向的流动(U,V)，主要关注Z方向(W)的流动问题。
流动只考虑z方向，但是粘性项需要考虑x和y方向。由于网格是随着之间变化的，因此控制方程应该需要进行修改，这个部分理论不足，真不知道如何处理？希望能够有这方面的行家交流学习一下，谢谢谢谢~

李东岳

没太看明白你的意思，最近在准备OKSS2的求解器，你在icoFoam里面，添加两个信息：

mesh.update()函数处理网格变形
通过phi = phi - mesh.phi()将通量变为相对通量代入到动量方程，压力方程不变

就可以了

从算法来讲，静态网格：
\begin{equation}
\frac{\p \rho}{\p t}+\nabla\cdot\rho\bfU=0,
\label{C}
\end{equation}
\begin{equation}
\frac{\partial \mathbf{U}}{\partial t}+\nabla \cdot (\mathbf{U} \otimes\mathbf{U})=-\nabla \frac{p}{\rho}+\nabla \cdot(\nu \nabla \mathbf{U}),
\label{mom}
\end{equation}
对于动态网格，需要考虑相对速度通量，则变为：
\begin{equation}
\frac{\p \rho}{\p t}+\nabla\cdot\rho(\bfU-\bfU_b)=0,
\label{C2}
\end{equation}
\begin{equation}
\frac{\partial \mathbf{U}}{\partial t}+\nabla \cdot (\mathbf{U} (\bfU-\bfU_b))=-\nabla \frac{p}{\rho}+\nabla \cdot(\nu \nabla \mathbf{U}),
\label{mom2}
\end{equation}
同时附加空间守恒法则：
\begin{equation}
\frac{\p \rho}{\p t}-\nabla\cdot\rho\bfU_b=0,
\label{SCL}
\end{equation}
把\eqref{SCL}代入到\eqref{C2}变成了：
\begin{equation}
\nabla\cdot\rho\bfU=0,
\label{C3}
\end{equation}
这样，\eqref{C3}用来构建压力泊松方程，\eqref{mom2}用来构建动量方程，求解即可

winsway_zero

@东岳谢谢东岳老师，我明白如何处理了哈。东岳老师整理的文档和资料都很通俗易懂。

CFD中文网

关于动网格的求解方法及步骤咨询