LES定义入口速度的问题(DSRFG方法)
-
@霜染丹枫
我做的风场模拟,所以我检察风洞模拟是否正确是通过检察计算域内的风速时程的功率谱是否和目标谱一致,也就是是否和在入口处生成的风速满足同样的能量分布。
不知道你们槽流最关心的是哪一个数值特征。比如,你可以验证turbulence intensity也可以验证power spectra,但不能通过一个瞬态的流场来判断模拟的好坏。一直不清楚你通过离散能量谱得到的脉动速度为什么要通过观察瞬时速度场来判断模拟的好坏,就算有很强的紊流特性也不能保证这个速度场的能量分布就和你目标谱一样。
上文中@sunss 同学说的那个tinf,你可以看一下,其中有dfsem, dfm等方法,特别是对于槽流,openfoam的tutorial中有一个RE395的算例(也许把名字记错了),应用的是DFSEM方法。
如@sunss 同学所说,也许高斯谱更适合你的功率谱,这样的话你可以直接应用fluent自带的那个对应RFG(Smirnov et al,2001)的生成方法,具体名字不记得了,你可以自己去查一下。
在其他回复中我提到过,DSRFG方法虽然理论上来说是无散度的,但如果应用在数值模拟中,就不是严格的无散度了,需要考虑网格尺寸,所以我一开始就问你网格尺寸和紊流积分尺度的数值。我们完成了一篇这样的论文,希望早点可以和你们分享。 -
各位老师专家好,我目前在做ABL的LES湍流入口时也碰到一些问题想和大家交流学习。我之前一直用Fluent来生成LES的湍流入口,近半年开始对Openfoam感兴趣,于是开始尝试把Fluent的相关算法移植到Openfoam当中,我采用的算法是华南理工杨易老师课题组提出的NSRFG算法,参考文献:
[1] Yu Y, Yang Y, Xie Z. A new inflow turbulence generator for large eddy simulation evaluation of wind effects on a standard high-rise building[J]. Building and Environment, 2018, 138: 300-313.
先把Fluent和of的计算结果图贴两张,我主要对PSD和湍流强度与平均风剖面进行了验证。
计算域
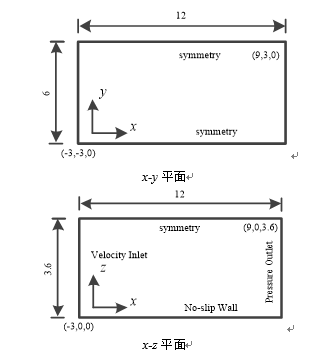
-
Fluent流场图及验证图
P1 是入口处的测点,P2是模型处的测点
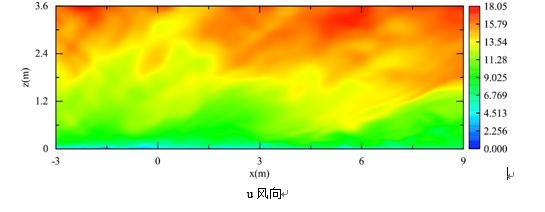
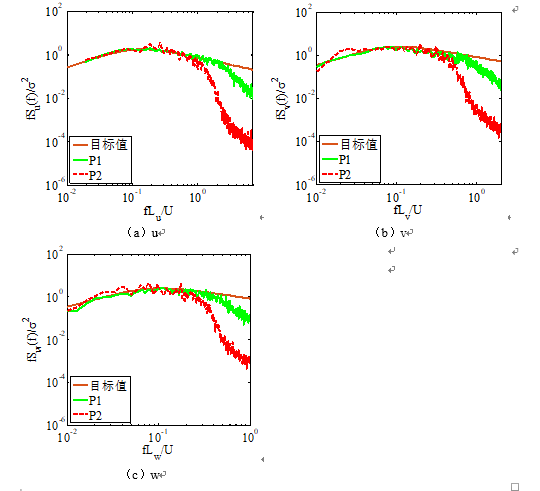
-
Openfoam流场图与验证图

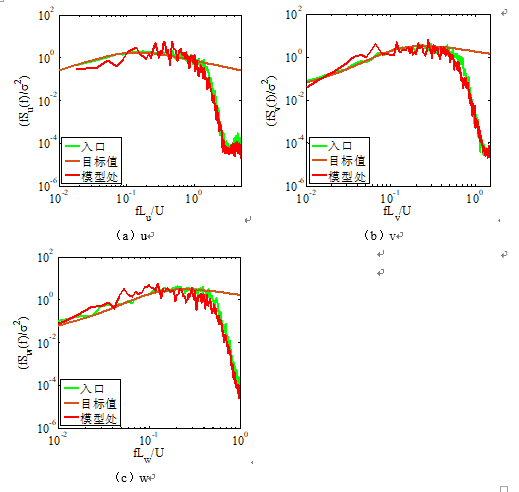
这里貌似of的结果还行,但实际上我认为Fluent的结果更合理,因为数值耗散等因素的影响,湍动能一定会在计算过程中耗散,因此模型处的PSD一定会更加吻合目标值。所以我目前怀疑我的case设置有问题,目前我采用的LES是WALE模型,0文件夹下应该要设置k 和 nut两个文件,我的设置分别如下:
/*--------------------------------*- C++ -*----------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | Website: https://openfoam.org \\ / A nd | Version: 6 \\/ M anipulation | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object k; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -2 0 0 0 0]; internalField uniform 0.0001; boundaryField { inlet { type fixedValue; value uniform 0; } ground { type kLowReWallFunction; //For high and low Re value $internalField; } top { type symmetry; } side1 { type symmetry; } side2 { type symmetry; } outlet { type zeroGradient; } } /*--------------------------------*- C++ -*----------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | Website: https://openfoam.org \\ / A nd | Version: 6 \\/ M anipulation | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object nut; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -1 0 0 0 0]; internalField uniform 1e-8; boundaryField { inlet { type zeroGradient; } ground { type nutUSpaldingWallFunction; value uniform 1e-8; } top { type symmetry; } side1 { type symmetry; } side2 { type symmetry; } outlet { type zeroGradient; } } // ************************************************************************* //这里我不太确定两个文件中internalField参数应该如何取值?另外,这两个参数对结果影响是否很大?请各位老师专家解答。谢谢!(P.S. of计算速度是真的快)
-
-
@xiaoyi0830 在 LES定义入口速度的问题(DSRFG方法) 中说:
@coolhhh 对于第一个问题,我也是晕了,三维能谱,一维能谱,功率谱怎么在这儿就混用了。
另外第四个问题,就算满足了连续性条件,也不会满足动量方程,所以进入计算域的速度肯定和入口处是有差别的。
-
@xiaoyi0830
1、功率谱计算。时间序列$ x(t) $计算时间相关函数$ R_{xx}(\tau) $,再进行傅里叶变换得到功率谱$ S_{xx}(\omega) $。
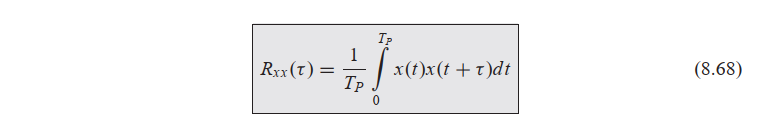
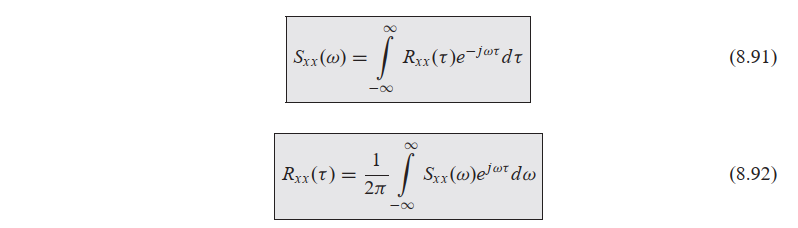
(引用:Shin K, Hammond J. Fundamentals of signal processing for sound and vibration engineers[M]. England: John Wiley & Sons, 2008:245.)2、风速功率谱。风速时程$ u(t) $对应时间序列$ x(t) $,求得的一维频谱(频域)就是对应此处的功率谱。一维频谱的自变量是频率或者角频率。
3、三维谱(波数域)。首先对三维空间相关函数进行三维的傅里叶变换得到的三维波谱,然后进行球面积分并乘以系数1/2,得到三维谱。因此要计算一个三维谱,需要整个三维空间的所有点的风速时程才能计算得到一个三维谱。


(引用:田内科斯 H., 兰姆利 J. L. 湍流初级教程[M]. 北京: 科学出版社, 2014:194-197.)4、一维波谱(波数域)。一维波谱是由一维空间相关函数(即一个空间方向的相关函数),进行一维的傅里叶变换得到的。与一维频谱类似,只是一个是频域,一个是波数域。
5、三维von Karman谱(均匀流场)表达式如下。针对于非均匀流场的三维von Karman谱表达式,个人未找到相关文章阐述。

(引用:Durbin P A, Pettersson Reif B A. Statistical theory and modeling for turbulent flows[M].Wiley, 2011:29-261.)6、三维von Karman谱与一维von Karman谱区别。
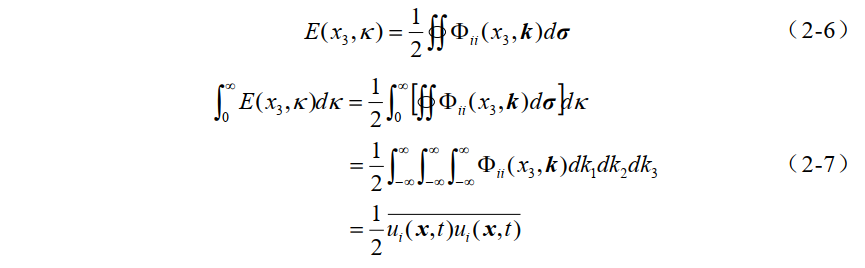
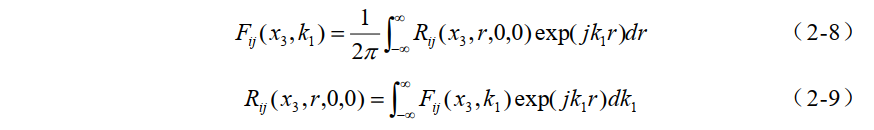

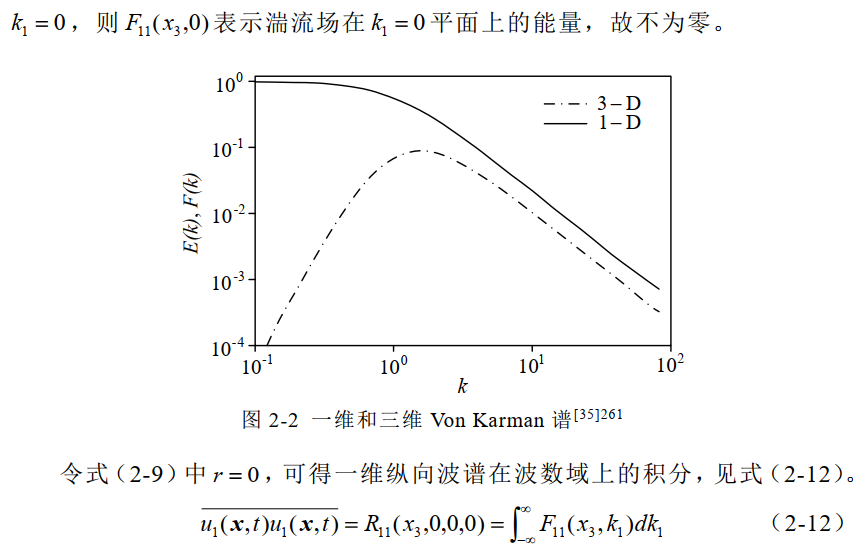

(引用:[1] Durbin P A, Pettersson Reif B A. Statistical theory and modeling for turbulent flows[M].Wiley, 2011:29-261.
[2] 陈铃伟. 基于傅里叶合成法的大气边界层脉动风场大涡模拟[D]. 黑龙江:哈尔滨工业大学,2017. DOI:10.7666/d.D01589559.)7、从《Diffusion by a Random Velocity Field》(Kraichan, 1970),到RFG方法,论文中都是未出现频谱的图,因为方法本身目标就是生成三维谱。DSRFG方法的理论推导也是实现三维谱,但是在应用方法时,用一维频谱表示三维谱,并最终的结果用频谱图表示,这与三维谱的原始定义是不同概念的,这两者不应该混淆。
8、CDRFG、NSRFG的理论推导就是为实现一维频谱。CDRFG方法既然目标实现频谱,可以简化一个循环,如下阐述
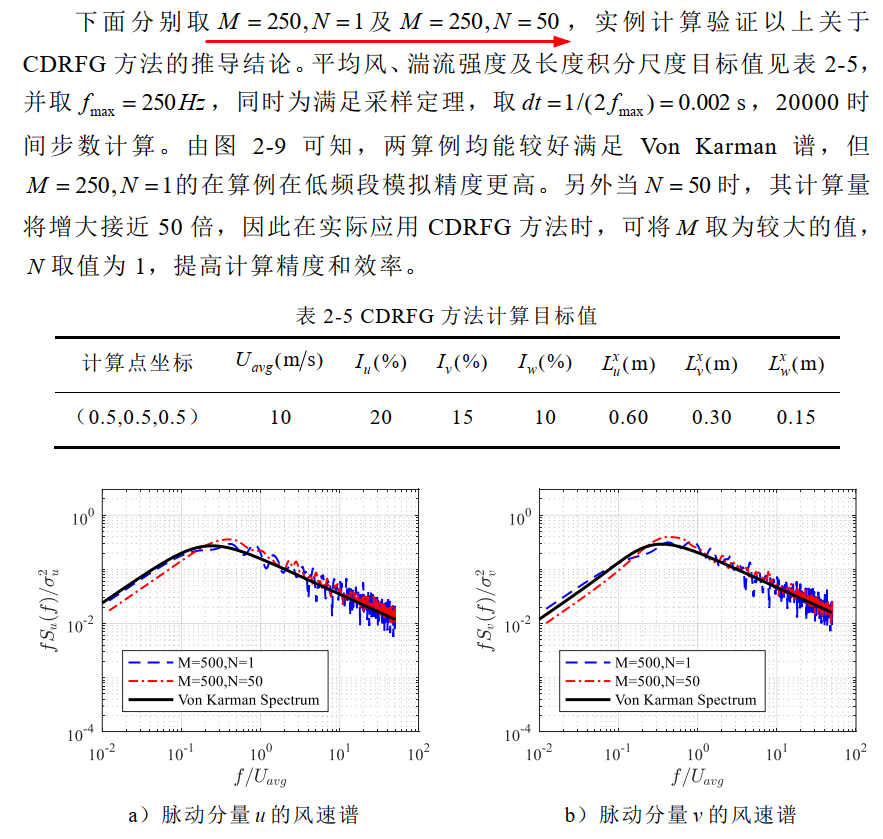
(引用:陈铃伟. 基于傅里叶合成法的大气边界层脉动风场大涡模拟[D]. 黑龙江:哈尔滨工业大学,2017. DOI:10.7666/d.D01589559.)9、CDRFG方法的P、Q的原论文的公式有误,在原作者后来发的一篇文章中已对其进行了更正。
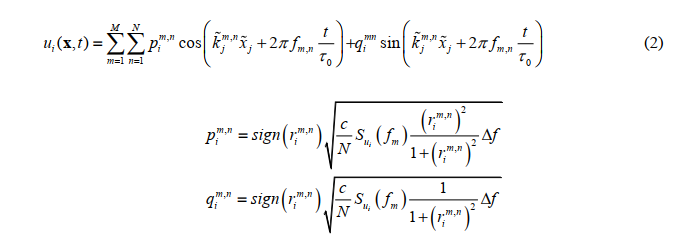
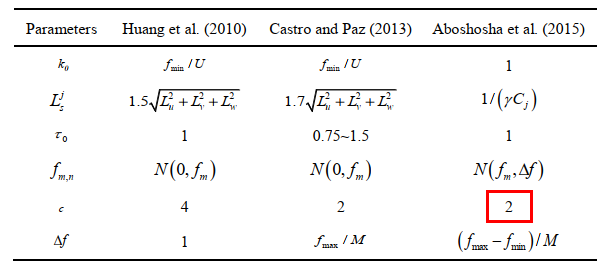
(引用:Melaku A, Bitsuamlak G, Elshaer A, et al. Synthetic inflow turbulence generation methods for LES study of tall building aerodynamics[J]. 2017.) -
NSRFG湍流入口合成方法分享(我在验证结果的时候发现NSRFG方法和CDRFG方法均存在水平方向流场均一性问题,不知道对不对)。
%% NSRFG湍流合成方法 tic clc,clear %%生成0-fmax Hz范围的功率谱 fmax=25;df=0.001;fw=df:df:fmax; N=length(fw); fm=(2*(1:N)-1)/2*df; Time_NSRFG=1000;%时间点数量 h=1/fmax/2;%时间步长 Fs=1/h; %%入口尺寸和模拟点数量设置 x=1;%流场方向坐标 y=1;%水平方向坐标 z=[linspace(0.01,0.1,10),linspace(0.11,0.5,20),linspace(0.55,1,10)];%竖直方向坐标 N0_Y=length(y);N0_Z=length(z);N0_X=length(x);%X,Y,Z对应u,v,w,各方向上的点数 xyz=[repmat(x,length(z)*length(y),1),... repmat(y',length(z),1),... reshape(repmat(z,length(y),1),[],1)]'; %%切分Time_NSRFG成N0_T段,避免内存溢出 memory_capacity=0.4*10^9;%16G内存建议取值,内存越大计算速度越快 N0_t=min(fix(memory_capacity/(N0_Z*N0_Y)/N),Time_NSRFG); N0_T=ceil(Time_NSRFG/N0_t); %%相关性参数设置, c_1=10;c_2=12;c_3=12; Gammaix=1.8;Gammaiy=1.5;Gammaiz=1.8; %%风场特性-风速 z_ref=0.4;%标准参考高度 alpha=0.25;%粗糙度指数 U_ref=10.0;%参考风速 I_10=0.23; coefv=0.88; coefw=0.55; Uav=U_ref*(z/z_ref).^alpha; Uav_map=(reshape(repmat(Uav,N0_Y,1),[],1))'; %%风场特性-湍流强度 Iu=0.1*(z/z_ref).^(-alpha-0.05); Iv=coefv*Iu; Iw=coefw*Iu; I_map=[(reshape(repmat(Iu,N0_Y,1),[],1)),... (reshape(repmat(Iv,N0_Y,1),[],1)),... (reshape(repmat(Iw,N0_Y,1),[],1))]';= %%风场特性-积分尺度 z_0=0.25; Lu=linspace(0.25,1,N0_Z); Lv=0.5*coefv^3*Lu; Lw=0.5*coefw^3*Lu; L_map=[(reshape(repmat(Lu,N0_Y,1),[],1)),... (reshape(repmat(Lv,N0_Y,1),[],1)),... (reshape(repmat(Lw,N0_Y,1),[],1))]'; %初始化参数 Su=zeros(N,N0_Z*N0_Y);Sv=zeros(N,N0_Z*N0_Y);Sw=zeros(N,N0_Z*N0_Y); p_uvw=zeros(3,N); p_u=zeros(N,N0_Z*N0_Y);p_v=zeros(N,N0_Z*N0_Y);p_w=zeros(N,N0_Z*N0_Y); Lx=zeros(N,N0_Z*N0_Y);Ly=zeros(N,N0_Z*N0_Y);Lz=zeros(N,N0_Z*N0_Y); q_1n=zeros(N,N0_Z*N0_Y);q_2n=zeros(N,N0_Z*N0_Y);q_3n=zeros(N,N0_Z*N0_Y); A_n=zeros(N,N0_Z*N0_Y);B_n=zeros(N,N0_Z*N0_Y); k_1n=zeros(N,N0_Z*N0_Y);k_2n=zeros(N,N0_Z*N0_Y);k_3n=zeros(N,N0_Z*N0_Y); K_xyz=zeros(3,N0_Z*N0_Y,N); x_1n=zeros(N,N0_Z*N0_Y);x_2n=zeros(N,N0_Z*N0_Y);x_3n=zeros(N,N0_Z*N0_Y); X_xyz=zeros(3,N0_Z*N0_Y,N); U_u0=zeros(N0_t,N0_Z*N0_Y,N);U_v0=zeros(N0_t,N0_Z*N0_Y,N);U_w0=zeros(N0_t,N0_Z*N0_Y,N); U_u=zeros(1,N0_Z*N0_Y);U_v=zeros(1,N0_Z*N0_Y);U_w=zeros(1,N0_Z*N0_Y); %球面随机采样 S = randn(N,3); sign_n =bsxfun(@rdivide, S, sqrt(sum(S.*S, 2))); plot3(sign_n(:,1),sign_n(:,2),sign_n(:,3),'.k', 'MarkerSize',10) %绘制原始散点数据 %%生成随机数\thea_n thea_n=2*pi*rand(N+100,N0_Z*N0_Y); fm=(2*(1:N)-1)/2*df; %%生成参数矩阵 parfor n=1:N%频率范围 disp('n');disp(n); Su(n,:)=4*(I_map(1,:).*Uav_map).^2.*(L_map(1,:)./Uav_map)./... (1+70.8*(fm(n)*L_map(1,:)./Uav_map).^2).^(5/6);%Karman Sv(n,:)=4*(I_map(2,:).*Uav_map).^2.*(L_map(2,:)./Uav_map).*... (1+755.2*(fm(n)*L_map(2,:)./Uav_map).^2)./((1+283.2*(fm(n).*L_map(2,:)./Uav_map).^2).^(11/6));%Karman Sw(n,:)=4*(I_map(3,:).*Uav_map).^2.*(L_map(3,:)./Uav_map).*... (1+755.2*(fm(n)*L_map(3,:)./Uav_map).^2)./((1+283.2*(fm(n).*L_map(3,:)./Uav_map).^2).^(11/6));%Karman p_u(n,:)=sign(sign_n(n,1))*sqrt(2*Su(n,:)*df); p_v(n,:)=sign(sign_n(n,2))*sqrt(2*Sv(n,:)*df); p_w(n,:)=sign(sign_n(n,3))*sqrt(2*Sw(n,:)*df); Lx(n,:)=U_ref./((fm(n)))./c_1./Gammaix; Ly(n,:)=U_ref./((fm(n)))./c_2./Gammaiy; Lz(n,:)=U_ref./((fm(n)))./c_3./Gammaiz; q_1n(n,:)=p_u(n,:)./Lx(n,:); q_2n(n,:)=p_v(n,:)./Ly(n,:); q_3n(n,:)=p_w(n,:)./Lz(n,:); A_n(n,:)=sqrt((q_2n(n,:).^2+q_3n(n,:).^2).^2+(q_1n(n,:).*q_2n(n,:)).^2+(q_1n(n,:).*q_3n(n,:)).^2); B_n(n,:)=sqrt(q_2n(n,:).^2+q_3n(n,:).^2); k_1n(n,:)=-(q_2n(n,:).^2+q_3n(n,:).^2)./A_n(n,:).*sin(thea_n(n,1)); k_2n(n,:)=(q_1n(n,:).*q_2n(n,:))./A_n(n,:).*sin(thea_n(n,1))+q_3n(n,:)./B_n(n,:).*cos(thea_n(n,1)); k_3n(n,:)=(q_1n(n,:).*q_3n(n,:))./A_n(n,:).*sin(thea_n(n,1))-q_2n(n,:)./B_n(n,:).*cos(thea_n(n,1)); div1(n,:)=q_1n(n,:).* k_1n(n,:)+q_2n(n,:).* k_2n(n,:)+q_3n(n,:).* k_3n(n,:); div2(n,:)= k_1n(n,:).* k_1n(n,:)+ k_2n(n,:).* k_2n(n,:)+ k_3n(n,:).* k_3n(n,:); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% K_xyz(:,:,n)=[k_1n(n,:);k_2n(n,:);k_3n(n,:)];%3x9 x_1n(n,:)=(xyz(1,:))./Lx(n,:); x_2n(n,:)=(xyz(2,:))./Ly(n,:); x_3n(n,:)=(xyz(3,:))./Lz(n,:); X_xyz(:,:,n)=[x_1n(n,:);x_2n(n,:);x_3n(n,:)];%3x9 kjxj(n,:)=(diag(K_xyz(:,:,n)'*X_xyz(:,:,n)))'; end;disp('完成构建矩阵'); %%合成风速 leq_n=2*pi*rand(3,N); t=(1:1:N0_t)*h; ru=sign_n(:,1);rv=sign_n(:,2);rw=sign_n(:,3); for it=1:N0_T for n=1:N disp(['N0_T--','it--','n','运行时间: ',num2str([N0_T,it,n,toc])]); U_u0(:,:,n)=p_u(n,:).*sin(repmat(kjxj(n,:),N0_t,1)+2*pi*fm(n).*t'+repmat(leq_n(1,n),N0_t,1)); U_v0(:,:,n)=p_v(n,:).*sin(repmat(kjxj(n,:),N0_t,1)+2*pi*fm(n).*t'+repmat(leq_n(1,n),N0_t,1)); U_w0(:,:,n)=p_w(n,:).*sin(repmat(kjxj(n,:),N0_t,1)+2*pi*fm(n).*t'+repmat(leq_n(1,n),N0_t,1)); end;t=t+N0_t*h; U_u=cat(1,U_u,sum(U_u0,3)); U_v=cat(1,U_v,sum(U_v0,3)); U_w=cat(1,U_w,sum(U_w0,3)); end U=roundn(U_u(2:end,:)+Uav_map,-4)'; V=roundn(U_v(2:end,:),-4)'; W=roundn(U_w(2:end,:),-4)'; toc disp(['运行时间: ',num2str(toc)]); disp('=====accomplish======') -
@xjwang 在 LES定义入口速度的问题(DSRFG方法) 中说:
@sunss
应该是在constant/boundaryData/inlet文件夹下边有一个points的文件,然后每一个时间步都是一个文件夹,其中包含一个U文件。比如说,我在inlet文件夹下边在terminal中输入ls,会显示:0 0.001 0.002 ...... points
而在每一个时间步文件夹下输入ls,比如在0.001文件夹下,会显示:
U
您好,我想请教一下这个数据的事情。在foam中运用并行运算,是在分块前面把inlet坐标输出然后运用算法求出inlet上每个点对应的风速,然后按照您的方法导入到constant/boundaryData/inlet中吗?还是在分块后,按照该方法进行呢?
