求助：Openfoam中的LES/DNS如何输出湍流耗散率
-
最近在备课，准备了很多湍流的东西，$\epsilon=\nu \overline{\dfrac{\partial u_{i}^{\prime}}{\partial x_{k}} \dfrac{\partial u_{i}^{\prime}}{\partial x_{k}}}$ 这个定义不是真正的epsilon的定义，真正的定义应该是$\epsilon=2\nu \overline{\bfS_{ij}'\bfS_{ij}'}=2\nu \overline{\bfS': \bfS'}=2\nu \overline{|\bfS'|^2}$。其中$\bfS'=\frac{1}{2}(\nabla\bfU'+\nabla\bfU'^T)$
所以在写代码的时候，大体就是：
- 通过求解器求解速度
U， - 通过fieldAverage获得
UMean - 二者相减是
U' - 通过
U'获得$\bfS'$ - 求解瞬态量$2\nu |\bfS'|^2$，对瞬态量$2\nu |\bfS'|^2$做平均。这个也可以在paraview里面通过滤镜来实现：
Filter-temporal-statistics
大体上，需要做两次平均过程。第一次平均获得uMean，第二次获得$\epsilon$定义里面的平均。这样可以获得解析的$\epsilon$。同时还要加上$\epsilon_{sgs}$。
可以参考Wilcox那本湍流书的109页。
我算了算$Re_\tau=395$的算例，左边是湍流动能耗散率，右边是速度。看起来是符合物理的。就是没有数据可以对。
- 通过求解器求解速度
-
-
@李东岳 李老师您好~
求得时均速度之后，就可以用时均速度和当前时间步的脉动速度求瞬时的脉动速度应变率张量S’，可以直接对S’求双内积（&&）嗷，为什么要用这一步呢？
-
@xiexiaoyang 嗯？没懂
-
@李东岳 !李老师，就是这样：
求得脉动速度后，直接做双内积，然后把这个标量场存下来，再用fieldAverage做时间平均。 -
@xiexiaoyang 我求的是这个：$\epsilon=2\nu \overline{|\bfS'|^2}$，不是$\epsilon=\nu \overline{\dfrac{\partial u_{i}^{\prime}}{\partial x_{k}} \dfrac{\partial u_{i}^{\prime}}{\partial x_{k}}}$。这两个有点区别，但是结果应该差不多。你试试channel395，看看结果如何？
-
@李东岳" class=" img-fluid img-markdown">
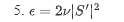
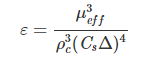
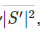做时间平均 没有对粘性项做平均