为什么压力泊松方程离散后的矩阵是非对角占优的啊?
-
对于泊松方程,由拉普拉斯算子离散而来,有两个特性,一个是离散后形成的矩阵对阵,另一个是非对角占优,正常来说,我们希望矩阵对称,并且对角占优,有利于在应用迭代法求解线性方程组过程中的收敛,此时称为矩阵的性质好?我想请教下,大佬们,有没有什么数学上或理论上的证明,或者说,什么条件下离散后的矩阵才具有对角占优的性质?为什么压力泊松方程是非对角占有的啊?谢谢!
附录:常见的求解变量的对上述两个条件满足状况如下压力方程 p(不可压缩非稳态流动) :对称矩阵,但对角相等,非对角占优,因此计算量较大。速度方程 U(不可压缩非稳态流动) :非对称矩阵,对角占优,计算量通常较 p 小。一般标量方程 k,epsilon,T 等(非稳态流动):非对称矩阵,对角占优,计算量较小。非稳态纯扩散方程(比如纯导热问题):对称矩阵,对角占优,计算量最小;因此,在计算过程中,可以对压力方程 p 选择“共轭梯度求解器+代数多重网格预条件器”而速度 U 和其他标量方程选择一般的共轭梯度求解器。
-
之所以压力泊松方程离散出来之后得到的矩阵是对称的且不是严格对角占优,是因为通常泊松方程里面的 laplacian 项是用中心差分来离散的。楼主看一下 src/finiteVolume/finiteVolume/laplacianSchemes/gaussLaplacianScheme里面 fvmLaplacian 函数的定义就明白了。
动量方程为什么对角占优呢?主要来自于- 对流项,特定的对流项格式可以保证离散之后对角占优
- 时间项,时间项的离散得到的系数只会进入系数矩阵的主对角。
- 隐式松弛,从构建系数矩阵的角度来看,隐式松弛和时间项达到的效果一样,都会增加对角占优
- 特殊的源项,比如 fvm::Sp 得到的隐式源项,也是只贡献于系数矩阵的对角元素,可以增加对角占优(不正确使用则会减弱对角占优)。
-
@xpqiu 好的!非常感激xpqiu教授的精彩细致的回复,那我可不可以根据您的回答总结这样一句话:单纯含有扩散项的方程离散后得到的矩阵性质并不好(因为不是严格对角占优的)。可是为什么下面的图片好像不太支持这样的结论呢?
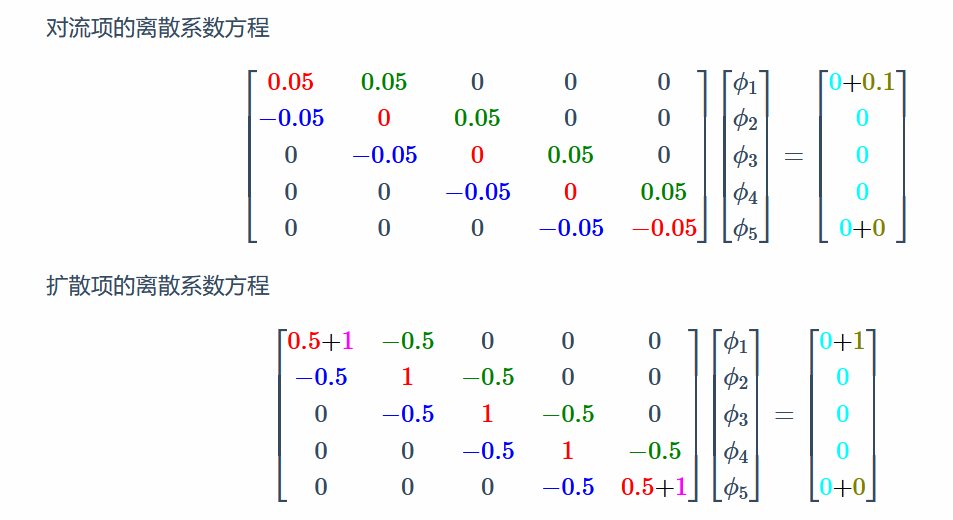
您看,如果所示,这是一个一维对流扩散方程离散后的结果,其中,对流项对应的矩阵性质很不好(对角不占优且不对称),而扩散项离散后得到的矩阵确实严格对角占优的,具体网站:https://marinecfd.xyz/post/from-geometricfield-to-fvmatrix
请问为什么会出现相反的结果呢?希望您有时间能再稍微回复下!万分感谢!
