尝试compressibleInterFoam温度方程推导遇阻
-
老师好,我尝试推导compressibleInterFoam中的温度方程,但推导出来的结果与求解器中的温度方程有差异(多了两项),请教是否推导过程有误。
求解器中的温度方程:
$$
\frac{\partial }{\partial t}(\rho T)+\nabla \cdot (\rho \boldsymbol{U} T)=\nabla \cdot (\alpha_{eff} \nabla T) - (\frac{\alpha_{1}}{c_{v,1}}+\frac{\alpha_{2}}{c_{v,2}}) \left(\nabla \cdot (\boldsymbol{U} p) + \frac{\partial}{\partial t} (\rho K) + \nabla \cdot (\rho \boldsymbol{U} K) \right)
$$
对应代码:fvScalarMatrix TEqn ( fvm::ddt(rho, T) + fvm::div(rhoPhi, T) - fvm::Sp(contErr, T) - fvm::laplacian(turbulence.alphaEff(), T) + ( fvc::div(fvc::absolute(phi, U), p)()() // - contErr/rho*p + (fvc::ddt(rho, K) + fvc::div(rhoPhi, K))()() - contErr*K ) *( alpha1()/mixture.thermo1().Cv()() + alpha2()/mixture.thermo2().Cv()() ) == fvOptions(rho, T) );推导过程过程:
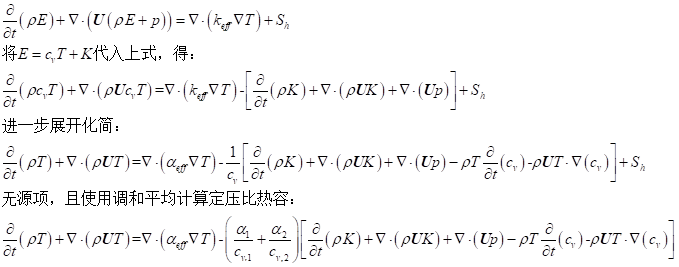
可见,最后在右边多了两项:
$$
(\frac{\alpha_{1}}{c_{v,1}}+\frac{\alpha_{2}}{c_{v,2}}) \left( \rho T \frac{\partial c_{v}}{\partial t} + \rho \boldsymbol{U} T \cdot \nabla c_{v} \right)
$$
其中,$\frac{1}{c_{v}}=\frac{\alpha_{1}}{c_{v,1}}+\frac{\alpha_{2}}{c_{v,2}}$.
